2019 Multi-University Training Contest 10 HDU多校赛 题解
HDU 6691 01.Minimum Spanning Trees
题意
给n个点,每条边的权值有一定概率出现,题目给出。权值为0表示不存在。问对于若干个S求最小生成树恰好为S的概率。
题解
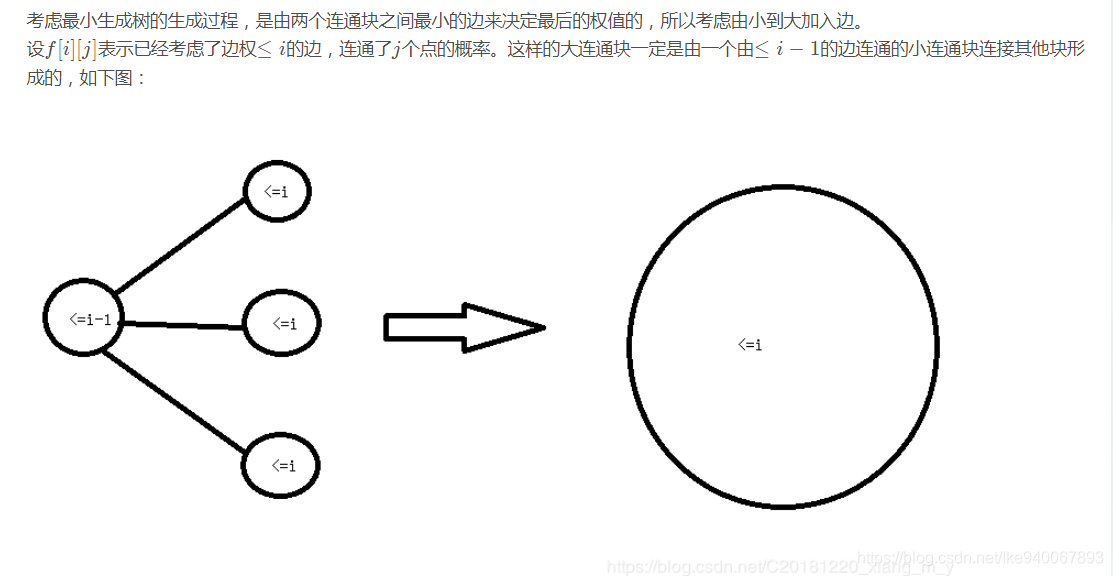


转自 Master.Yi的博客
CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 50;
const int MAXK = 6;
const int mod = 1e9 + 7;
const int inv100 = 570000004;
inline int qpow(int a, int b) {
int re = 1;
while(b) {
if(b&1) re = 1ll * re * a % mod;
a = 1ll * a * a % mod; b >>= 1;
}
return re;
}
inline int mul(int x, int y) { return 1ll * x * y % mod; }
inline int add(int x, int y) { return (x + y) % mod; }
int c[MAXN][MAXN], inv[MAXN*MAXK], p[MAXK], sp[MAXK], pwx[MAXK];
int t1[MAXN][MAXN], t2[MAXN][MAXN], f[MAXK][MAXN], g[MAXN][MAXN];
int v[MAXN*MAXK];
vector<int>interpolation(int y[], int n) { //拉格朗日插值求多项式系数
vector<int>P(n+1), now(n+1), re(n); P[0] = 1;
for(int i = 0; i < n; ++i) for(int j = i+1; ~j; --j) P[j] = add(j?P[j-1]:0, -mul(i, P[j]));
for(int i = 0; i < n; ++i) {
for(int j = n-1; ~j; --j) now[j] = add(P[j+1], mul(i, now[j+1]));
int tmp = (((n-i-1)&1)?-1:1) * mul(mul(inv[i], inv[n-i-1]), y[i]);
for(int j = 0; j < n; ++j) re[j] = add(re[j], mul(tmp, now[j]));
}
return re;
}
void solve() {
int n, k;
scanf("%d%d", &n, &k);
for(int i = 0; i <= k; ++i) scanf("%d", &p[i]), p[i] = mul(p[i], inv100);
sp[k+1] = 0;
for(int i = k; ~i; --i) sp[i] = add(sp[i+1], p[i]);
for(int x = 0; x <= (k-1)*(n-1); ++x) {
pwx[0] = 1;
for(int i = 1; i < k; ++i) pwx[i] = mul(pwx[i-1], x);
f[0][1] = 1;
for(int t = 1; t <= k; ++t) {
for(int i = 0; i <= n; ++i)
for(int j = 1; i+j <= n; ++j) {
t2[i][j] = qpow(p[0] + sp[t+1], i*j); //用>t的边
t1[i][j] = add(qpow(p[0] + sp[t], i*j), -t2[i][j]); //用>=t的边且至少一条=t
}
for(int i = 1; i <= n; ++i)
for(int j = 0; i+j <= n; ++j)
g[i][j] = (j == 0);
for(int s = 1; s <= n; ++s) {
f[t][s] = 0;
for(int i = 1; i <= s; ++i)
f[t][s] = add(f[t][s], mul(mul(f[t-1][i], g[i][s-i]), c[s-1][i-1]));
for(int i = 1; i <= n; ++i)
for(int j = n-i-s; j >= 0; --j)
for(int k = 1, tmp = 1, bas = mul(pwx[t-1], mul(t1[i][s], f[t][s])); i+j+k*s <= n; ++k) {
tmp = mul(tmp, mul(bas, mul(t2[j+(k-1)*s][s], c[j+k*s][s])));
g[i][j+k*s] = add(g[i][j+k*s], mul(mul(g[i][j], tmp), inv[k]));
}
}
}
v[x] = f[k][n];
//printf("v(%d) = %d\n", x, v[x]);
}
vector<int>ans = interpolation(v, (k-1)*(n-1)+1);
for(int i = 0; i <= (k-1)*(n-1); ++i)
printf("%d%c", add(ans[i], mod), " \n"[i==(k-1)*(n-1)]);
}
void pre() {
c[0][0] = 1;
for(int i = 1; i < MAXN; ++i) {
c[i][0] = c[i][i] = 1;
for(int j = 1; j < i; ++j)
c[i][j] = add(c[i-1][j-1], c[i-1][j]);
}
inv[0] = inv[1] = 1;
for(int i = 2; i < MAXN*MAXK; ++i)
inv[i] = mul(mod - mod/i, inv[mod%i]);
for(int i = 2; i < MAXN*MAXK; ++i)
inv[i] = mul(inv[i], inv[i-1]);
}
int main() {
pre();
int T; scanf("%d", &T);
while(T-->0)solve();
}
HDU 6693 03.Valentine’s Day
题意
略
题解
显然从大到小贪心,买进来能够让答案更优就买。如果一个买不了剩下的一定也买不了,直接break就行了。
CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 10005;
int n;
double p[MAXN];
int main () {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d", &n);
for(int i = 1; i <= n; ++i)
scanf("%lf", &p[i]);
sort(p + 1, p + n + 1);
double ans = p[n], tmp = 1-p[n];
for(int i = n-1; i; --i) {
if(ans * (1-p[i]) + tmp * p[i] > ans) {
ans = ans * (1-p[i]) + tmp * p[i];
tmp *= 1-p[i];
}
else break;
}
printf("%.12f\n", ans);
}
}
HDU 6694 04.Play Games with Rounddog
题意+题解
CODE
又双叒叕学习了一发SAM
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
const int MAXN = 200005;
LL W[MAXN];
char s[MAXN];
int pos[MAXN], Right[MAXN], dep[MAXN], f[MAXN][19], c[MAXN];
vector<int>G[MAXN];
struct Linear_Basis {
LL a[58]; ULL ans;
inline void init() { ans = 0; memset(a, 0, sizeof a); }
inline bool ins(LL x) {
LL tmp = x;
for(int i = 57; ~i; --i)
if(x&(1ll<<i)) {
if(!a[i]) { a[i] = x; ans += tmp; return 1; }
x ^= a[i];
}
return 0;
}
}LB[MAXN];
struct Suffix_Automation {
int tot, cur;
struct node{ int len, fa, ch[26]; } t[MAXN];
inline void init() {
cur = tot = 1;
memset(t, 0, sizeof t);
memset(Right, 0, sizeof Right);
}
inline void ins(int x) {
int p = cur; ++Right[cur = ++tot]; t[cur].len = t[p].len + 1;
for(; p && !t[p].ch[x]; p = t[p].fa) t[p].ch[x] = cur;
if(!p) { t[cur].fa = 1; return; }
int q = t[p].ch[x];
if(t[p].len + 1 == t[q].len) { t[cur].fa = q; return; }
int clone = ++tot;
t[clone].len = t[p].len + 1;
memcpy(t[clone].ch, t[q].ch, sizeof t[q].ch);
t[clone].fa = t[q].fa;
t[q].fa = t[cur].fa = clone;
for(; p && t[p].ch[x] == q; p = t[p].fa) t[p].ch[x] = clone;
}
void dfs(int u) {
for(int v, i = G[u].size()-1; ~i; --i) {
v = G[u][i];
dep[v] = dep[u] + 1;
f[v][0] = u;
dfs(v);
Right[u] += Right[v];
}
}
inline void build() {
memset(G, 0, sizeof G);
for(int i = 2; i <= tot; ++i) G[t[i].fa].push_back(i);
dfs(1);
for(int j = 1; j < 19; ++j)
for(int i = 1; i <= tot; ++i)
f[i][j] = f[f[i][j-1]][j-1];
}
}SAM;
inline bool cmp(int i, int j) { return W[Right[i]] > W[Right[j]]; }
int main() {
int T, n, q, x, y; scanf("%d", &T);
while(T-->0) {
scanf("%d%s", &n, s+1);
SAM.init();
for(int i = 1; i <= n; ++i)
SAM.ins(s[i]-'a'), pos[i] = SAM.cur;
for(int i = 1; i <= n; ++i) scanf("%lld", &W[i]);
SAM.build();
int tot = SAM.tot;
for(int i = 1; i <= tot; ++i)
LB[i].init(), c[i] = i;
sort(c + 1, c + tot + 1, cmp);
for(int i = 1; i <= tot; ++i)
for(int p = c[i]; p; p = f[p][0])
if(!LB[p].ins(W[Right[c[i]]])) break;
scanf("%d", &q);
while(q-->0) {
scanf("%d%d", &x, &y);
int len = y-x+1, p = pos[y];
for(int i = 18; ~i; --i)
if(SAM.t[f[p][i]].len >= len) p = f[p][i];
printf("%llu\n", LB[p].ans);
}
}
}
HDU 6695 05.Welcome Party
题意
略
题解
枚举第一个集合的x最大值k,那么另一个集合y的最大值一定要大于等于xi>k的所有yi
所以倒序枚举k,线段树维护就行了。
CODE
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
#define x first
#define y second
const int MAXN = 100005;
int n, nx, ny;
pair<LL,LL>p[MAXN];
LL vx[MAXN], vy[MAXN];
int Mn[MAXN<<2], Mx[MAXN<<2], cnt[MAXN];
void build(int i, int l, int r) {
Mn[i] = ny+1;
Mx[i] = 0;
if(l == r) { cnt[l] = 0; return; }
int mid = (l + r) >> 1;
build(i<<1, l, mid);
build(i<<1|1, mid+1, r);
}
void mdf(int i, int l, int r, int p, int v) {
if(l == r) {
cnt[p] += v;
if(!cnt[p]) Mn[i] = ny+1, Mx[i] = 0;
else Mn[i] = Mx[i] = l;
return;
}
int mid = (l + r) >> 1;
if(p <= mid) mdf(i<<1, l, mid, p, v);
else mdf(i<<1|1, mid+1, r, p, v);
Mn[i] = min(Mn[i<<1], Mn[i<<1|1]);
Mx[i] = max(Mx[i<<1], Mx[i<<1|1]);
}
int Min(int i, int l, int r, int L, int R) {
if(L <= l && r <= R) return Mn[i];
int mid = (l + r) >> 1, re = ny+1;
if(L <= mid) re = min(re, Min(i<<1, l, mid, L, R));
if(R > mid) re = min(re, Min(i<<1|1, mid+1, r, L, R));
return re;
}
int Max(int i, int l, int r, int L, int R) {
if(L <= l && r <= R) return Mx[i];
int mid = (l + r) >> 1, re = 0;
if(L <= mid) re = max(re, Max(i<<1, l, mid, L, R));
if(R > mid) re = max(re, Max(i<<1|1, mid+1, r, L, R));
return re;
}
int main () {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d", &n);
nx = ny = 0;
for(int i = 1; i <= n; ++i) {
scanf("%lld%lld", &p[i].x, &p[i].y);
vx[++nx] = p[i].x;
vy[++ny] = p[i].y;
}
sort(p + 1, p + n + 1);
sort(vx + 1, vx + nx + 1);
nx = unique(vx + 1, vx + nx + 1) - vx - 1;
sort(vy + 1, vy + ny + 1);
ny = unique(vy + 1, vy + ny + 1) - vy - 1;
for(int i = 1; i <= n; ++i) {
p[i].x = lower_bound(vx + 1, vx + nx + 1, p[i].x) - vx;
p[i].y = lower_bound(vy + 1, vy + ny + 1, p[i].y) - vy;
}
int cur = n, mx = 1; LL ans = 1ll<<62;
build(1, 1, ny);
for(int i = 1; i <= n; ++i) mdf(1, 1, ny, p[i].y, 1);
for(int i = n; i >= 1; --i) {
while(cur && p[cur].x > p[i].x) mx = max(mx, (int)p[cur].y), --cur;
mdf(1, 1, ny, p[i].y, -1);
int j = lower_bound(vy + mx, vy + ny + 1, vx[p[i].x]) - vy, tmp;
if(j <= ny && (tmp=Min(1, 1, ny, j, ny)) <= ny) ans = min(ans, vy[tmp] - vx[p[i].x]);
--j; if(j >= mx && (tmp=Max(1, 1, ny, mx, j)) >= mx) ans = min(ans, vx[p[i].x] - vy[tmp]);
mdf(1, 1, ny, p[i].y, 1);
}
printf("%lld\n", ans);
}
}
HDU 6696 06.Dense Subgraph
题意
一棵n个点的树,每个点有权值ai,一个连通诱导子图的密度定义为所有点权的平均值,你可以关闭一些点,然后树的美丽度定义为剩下的点的所有连通诱导子图(大于等于两个点)的密度的最大值。求使得树的美丽度<=X的关闭点的方案数。点的度数<=5
诱导子图的定义为点集V中的点之间的边都在边集E中的子图。在树上的连通诱导子图就是树上的一个连通块。
一句话题意:求删点的方案数,使得剩下的点数大于1的连通块的权值平均值的最大值小于等于X。
题解
首先观察到,从所有直径 ≤ 2 的子图中一定可以找到 density 最大的子图,否则沿着直径中间的边断开可以得到两棵至少有两个点的树,其中至少有一棵树的 density 不会更小。于是只需要考虑所有直径 ≤ 2 的子图,只有 个,每一个满足 density > x 子图中所有点不能同时亮。对每个点记录父亲、自己、以及每个儿子的状态,预处理出所有不合法状态之后在树上 dp 即可。
CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 35005;
const int mod = 1e9 + 7;
int n, X, a[MAXN], f[MAXN][3], tmp[10];
// self fa
//0 N ?
//1 Y N
//2 Y Y
vector<int>G[MAXN];
inline void mul(int &x, int y) { x = 1ll * x * y % mod; }
inline void add(int &x, int y) { x = (x + y) % mod; }
inline bool cmp(int x, int y) { return x > y; }
void dfs(int u, int ff) {
f[u][0] = 1; f[u][1] = f[u][2] = 0;
int siz = G[u].size();
for(int i = 0; i < siz; ++i)if(G[u][i] == ff){ swap(G[u][i], G[u][siz-1]); G[u].pop_back(); break; }
siz = G[u].size();
for(int v : G[u]) dfs(v, u), mul(f[u][0], (f[v][0] + f[v][1]) % mod);
for(int s = 0; s < 1<<siz; ++s) {
int g = 1, cur = 0;
for(int i = 0; i < siz; ++i)
if(s&(1<<i)) tmp[++cur] = a[G[u][i]], mul(g, f[G[u][i]][2]);
else mul(g, f[G[u][i]][0]);
if(!g) continue;
sort(tmp + 1, tmp + cur + 1, cmp);
int sum1 = a[u], sum2 = a[u] + a[ff];
bool flg1 = 1, flg2 = (sum2 <= X*2);
for(int i = 1; i <= cur && flg1; ++i)
flg1 &= ((sum1 += tmp[i]) <= (X*(i+1))),
flg2 &= ((sum2 += tmp[i]) <= (X*(i+2)));
if(flg1) {
add(f[u][1], g);
if(flg2) add(f[u][2], g);
}
}
}
int main() {
int T; scanf("%d", &T);
while(T --> 0) {
scanf("%d%d", &n, &X);
for(int i = 1; i <= n; ++i)
scanf("%d", &a[i]), G[i].clear();
for(int i = 1, x, y; i < n; ++i) {
scanf("%d%d", &x, &y);
G[x].push_back(y),
G[y].push_back(x);
}
dfs(1, 0);
printf("%d\n", (f[1][0] + f[1][1]) % mod);
}
}
HDU 6697 07.Closest Pair of Segments
题意
略
题解
二分答案+判断"线段"是否有交
然后写正解死活不过。
然后暴力+优化过了
650ms 目前hdu rk2
.
暴力艹正解
不过这个点到线段距离是自己写的,有点丑。更短的方法是点积判断钝角锐角,然后分类用叉积或者两点间距离算答案。
CODE
#include <bits/stdc++.h>
using namespace std;
typedef double db;
const double eps = 1e-8;
const int MAXN = 10005;
inline db sqr(db x) { return x*x; }
struct point {
db x, y; point(){}
point(db x, db y):x(x), y(y){}
inline point operator -(const point &o)const { return point(x-o.x, y-o.y); }
inline point operator +(const point &o)const { return point(x+o.x, y+o.y); }
inline point operator *(const db &o)const { return point(x*o, y*o); }
inline db mo() { return sqrt(sqr(x) + sqr(y)); }
};
struct line {
point u, v; line(){}
line(point u, point v):u(u), v(v){}
inline bool operator <(const line &o)const {
return u.x < o.u.x;
}
}L[MAXN];
inline db dis1(point A, point B) { return sqrt(sqr(A.x-B.x) + sqr(A.y-B.y)); }
inline db cross(point A, point B) { return A.x * B.y - A.y * B.x; }
inline db det(db A, db B, db C, db D) { return A * D - B * C; }
inline int sgn(double x) { return x > eps ? 1 : x < -eps ? -1 : 0; }
inline int sgndir(line A, point B) { return sgn(cross(A.v-A.u, B-A.u)); }
inline bool jiao(line A, line B) {
return sgndir(A, B.u) * sgndir(A, B.v) <= 0
&& sgndir(B, A.u) * sgndir(B, A.v) <= 0;
}
inline db dis2(point A, line B) {
point v2 = B.v - B.u, v1 = v2;
swap(v1.x, v1.y); v1.y=-v1.y; // rotate pi/2
// A + k1*v1 = B.u + k2*v2
double D = det(-v1.x, v2.x, -v1.y, v2.y);
assert(D);
double k1 = det(A.x-B.u.x, v2.x, A.y-B.u.y, v2.y) / D;
double k2 = det(-v1.x, A.x-B.u.x, -v1.y, A.y-B.u.y) / D;
if(k2 >= 0 && k2 <= 1) return fabs(k1) * v1.mo();
if(k2 < 0) return dis1(A, B.u);
return dis1(A, B.v);
}
inline db dis3(line A, line B) {
if(jiao(A, B)) return 0;
return min(min(dis2(A.u, B), dis2(A.v, B)), min(dis2(B.u, A), dis2(B.v, A)));
}
int n;
int main() {
int T; scanf("%d", &T);
while(T-->0) {
scanf("%d", &n);
for(int i = 1, A, B, C, D; i <= n; ++i) {
scanf("%d%d%d%d", &A, &B, &C, &D);
L[i] = line(point(A, B), point(C, D));
if(L[i].u.x > L[i].v.x) swap(L[i].u, L[i].v);
}
sort(L + 1, L + n + 1);
db ans = dis3(L[1], L[2]);
for(int i = 1; i <= n; ++i)
for(int j = i+1; j <= n; ++j) {
if(L[j].u.x - L[i].v.x > ans) break; //优化..
ans = min(ans, dis3(L[i], L[j]));
}
printf("%.12f\n", ans);
}
}
HDU 6698 08.Coins
题意
略
题解
放上官方题解:
- 先将硬币组分成两类,第一类 ai > bi,第二类 ai ≤ bi,并记 g(x) 为从第一类硬币中符合限制地取出 x 枚硬币的最大价值和,令 h(x) 为从第二类硬币中符合限制地取出 x 枚硬币的最大价值和。
- 要求出 g,只需要将第一类的所有硬币按价值从大到小排序,则 g(x) 为前 x 个硬币的和。因为 ai > bi,可以发现在这个贪心方法中,如果选了 bi,则一定会先选了 ai;
- 要求出 h,需要观察到:第二类硬币中最多只有一组硬币,会选了 ai 而没有选 bi。因为如果有两组硬币i, j, 满足 ai ≤ bi, aj ≤ bj,且某个方案只选了 ai, aj 而没有选 bi, bj,不失一般性,令 ai ≥ aj,那么有 bi ≥ ai ≥ aj,所以选 ai, bi 而不选 aj , bj 是个更优解,这时需要按 a + b 的值从大到小将第二类的每组硬币排序,则 h(2x) 就是前 x 组硬币的和,h(2x + 1) 就是“前 x 组加上不在前 x 组里的最大的 a”以及“前 x + 1 组中减去前 x + 1 组中最小的 b”两种方案中的较大值。
- 求出 g, h 之后, 立即有 ,朴素地计算这个 max 卷积只能做到 O(n^2),但是观察到 g 是个单调递增的凸函数而 h 是个单调递增函数,设 ,可以证明 p(x) 有单调性,利用决策单调性即可优化到 O(n log n)。
CODE
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
#define pii pair<int,int>
const int MAXN = 100005;
const int MAXM = 200005;
const int INF = 1<<30;
pii p[MAXN];
int g[MAXM], h[MAXM], f[MAXM];
int n, N, arr[MAXM], cur, tot;
inline bool cmpg(int a, int b) { return a > b; }
inline bool cmph(pii a, pii b) { return a.x+a.y > b.x+b.y; }
void Calc_g() {
memset(g, -0x7f, sizeof g); g[0] = 0;
sort(arr + 1, arr + cur + 1, cmpg);
for(int i = 1; i <= cur; ++i) g[i] = g[i-1] + arr[i];
}
int Mxa[MAXN], Mnb[MAXN];
void Calc_h() {
memset(h, -0x7f, sizeof h); h[0] = 0;
sort(p + 1, p + tot + 1, cmph);
Mxa[tot+1] = -INF;
for(int i = tot; i >= 1; --i) Mxa[i] = max(Mxa[i+1], p[i].x);
Mnb[0] = INF;
for(int i = 1; i <= tot; ++i) Mnb[i] = min(Mnb[i-1], p[i].y);
for(int i = 1; i <= tot; ++i)
h[i<<1] = h[(i-1)<<1] + p[i].x + p[i].y;
for(int i = 0; i <= tot; ++i) {
h[2*i+1] = max(h[2*i+1], h[i<<1] + Mxa[i+1]);
if(i)
h[2*i-1] = max(h[2*i-1], h[i<<1] - Mnb[i]);
}
}
int q[MAXM], k[MAXM];
int calc(int i, int j) { return h[j] + g[i-j]; }
int getk(int ii, int jj) {
int l = jj, r = N, mid;
while(l < r) {
mid = (l + r) >> 1;
if(calc(mid, ii) <= calc(mid, jj)) r = mid;
else l = mid+1;
}
if(calc(l, ii) <= calc(l, jj)) return l;
return r+1;
}
void Calc_f() {
f[0] = 0;
memset(k, 0, sizeof k);
int s = 1, t = 0;
q[++t] = 0;
for(int i = 1; i <= N; ++i) {
while(s < t && calc(k[t-1], q[t]) <= calc(k[t-1], i)) --t;
k[t] = getk(q[t], i); q[++t] = i;
while(s < t && k[s] <= i) ++s;
f[i] = calc(i, q[s]);
}
}
int main() {
int T; scanf("%d", &T);
while(T-->0) {
scanf("%d", &n); N = n<<1;
tot = cur = 0;
for(int i = 1, a, b; i <= n; ++i) {
scanf("%d%d", &a, &b);
if(a > b) arr[++cur] = a, arr[++cur] = b;
else p[++tot] = make_pair(a, b);
}
Calc_g(); Calc_h(); Calc_f();
for(int i = 1; i <= N; ++i)
printf("%d%c", f[i], " \n"[i==N]);
}
}
HDU 6699 09.Block Breaker
题意
略
题解
模拟
CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 2005;
int n, m, k, ans;
bool v[MAXN][MAXN];
void dfs(int x, int y) {
if(x < 1 || y < 1 || x > n || y > m || !v[x][y]) return;
if(v[x-1][y] + v[x+1][y] < 2 && v[x][y-1] + v[x][y+1] < 2) {
++ans;
v[x][y] = 0;
dfs(x+1, y);
dfs(x, y+1);
dfs(x-1, y);
dfs(x, y-1);
}
}
int main () {
int T;
scanf("%d", &T);
while(T--) {
scanf("%d%d%d", &n, &m, &k);
int x, y;
memset(v, 1, sizeof v);
while(k--) {
scanf("%d%d", &x, &y);
ans = 0;
if(v[x][y]) {
++ans;
v[x][y] = 0;
dfs(x+1, y);
dfs(x, y+1);
dfs(x-1, y);
dfs(x, y-1);
}
printf("%d\n", ans);
}
}
}
HDU 6701 11.Make Rounddog Happy
题意
略
题解
分治,考虑跨过最大值的区间。枚举较小的一边。预处理一些东西后就可以查询固定一个端点的答案。
需要预处理的:
1.st表求区间最大值
2.每个位置往左和往右最远能走多少没有相同的数字
CODE
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 300005;
const int LOG = 19;
long long ans;
int Lg[MAXN], n, k, a[MAXN], L[MAXN], R[MAXN], lst[MAXN];
pair<int,int>f[MAXN][LOG];
inline int qmx(int l, int r) {
int t = Lg[r-l+1];
return max(f[l][t], f[r-(1<<t)+1][t]).second;
}
void solve(int l, int r) {
if(l > r) return;
int pos = qmx(l, r), Min = max(a[pos]-k, 1);
if(pos-l < r-pos) {
for(int i = l, rr, ll; i <= pos; ++i) {
rr = min(r, R[i]);
ll = max(pos, i+Min-1);
ans += ll <= rr ? rr-ll+1 : 0;
}
}
else {
for(int i = r, ll, rr; i >= pos; --i) {
ll = max(l, L[i]);
rr = min(pos, i-Min+1);
ans += ll <= rr ? rr-ll+1 : 0;
}
}
solve(l, pos-1);
solve(pos+1, r);
}
signed main () {
Lg[0] = -1;
for(int i = 1; i < MAXN; ++i) Lg[i] = Lg[i>>1] + 1;
int T;
scanf("%d", &T);
while(T--) {
scanf("%d%d", &n, &k);
memset(lst, 0, sizeof lst);
int now = 1;
for(int i = 1; i <= n; ++i) {
scanf("%d", &a[i]), f[i][0] = make_pair(a[i], i);
if(lst[a[i]]) now = max(now, lst[a[i]]+1);
L[i] = now;
lst[a[i]] = i;
}
for(int j = 1; j <= Lg[n]; ++j)
for(int i = 1; i+(1<<j)-1 <= n; ++i)
f[i][j] = max(f[i][j-1], f[i+(1<<(j-1))][j-1]);
memset(lst, 0, sizeof lst);
now = n;
for(int i = n; i >= 1; --i) {
if(lst[a[i]]) now = min(now, lst[a[i]]-1);
R[i] = now;
lst[a[i]] = i;
}
ans = 0; solve(1, n);
printf("%lld\n", ans);
}
}
