算法与数据结构（五）树表的查找
*树表的查找*
（1）二叉排序树
（2）二叉排序树的操作——查找
（3）二叉排序树的操作——插入
（4）二叉排序树的操作——生成
（5）二叉排序树的操作——删除
（1）二叉排序树
由于线性表的查找更适合于静态查找表，若要对动态查找表进行高效率的查找，可采用二叉树作为查找表的组织形式，将其统称为树表。
二叉排序树又称二叉查找树，是一种对排序和查找都很有用的特殊二叉树。该表结构在查找过程中动态生成，对于给定值key 若表中存在，则成功返回； 否则插入关键字等于key 的记录。
二叉排序树或是空树，或是满足如下性质的二叉树：
(1)若其左子树非空，则左子树上所有结点的值均小于根结点的值；
(2)若其右子树非空，则右子树上所有结点的值均大于等于根结点的值；
(3)其左右子树本身又各是一棵二叉排序树。
☆中序遍历二叉排序树后的结果有什么规律？
答：得到一个关键字的递增有序序列
（2）二叉排序树的操作——查找
若查找的关键字等于根结点，成功 否则 若小于根结点，查其左子树 若大于根结点，查其右子树 在左右子树上的操作类似。
算法思想：
（1）若二叉排序树为空，则查找失败，返回空指针。
（2）若二叉排序树非空，将给定值key与根结点的关键字T->data.key进行比较：
① 若key等于T->data.key，则查找成功，返回根结点地址；
② 若key小于T->data.key，则进一步查找左子树；
③ 若key大于T->data.key，则进一步查找右子树。
代码：
1 BSTree SearchBST(BSTree T,KeyType key) { 2 if((!T) || key==T->data.key) return T; 3 else if (key<T->data.key) return SearchBST(T->lchild,key); 4 //在左子树中继续查找 5 else return SearchBST(T->rchild,key); 6 //在右子树中继续查找 7 } // SearchBST
（3）二叉排序树的操作——插入
若二叉排序树为空，则插入结点应为根结点 否则，继续在其左、右子树上查找 树中已有，不再插入 树中没有，查找直至某个叶子结点的左子树或右子树为空为止，则插入结点应为该叶子结点的左孩子或右孩子
插入的元素一定在叶结点上
例：插入结点20：
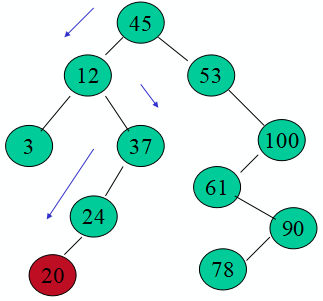
（4）二叉排序树的操作——生成
从空树出发，经过一系列的查找、插入操作之后，可生成一棵二叉排序树。
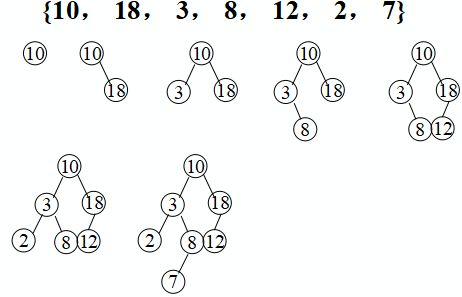
注意：不同插入次序的序列生成不同形态的二叉排序树
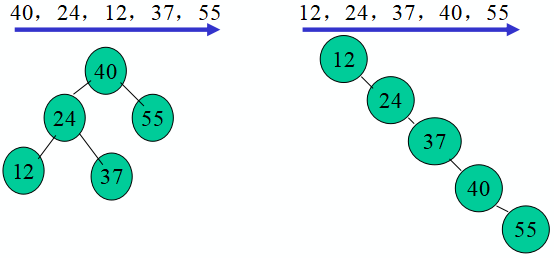
查找性能分析：
第i层结点需比较i次。在等概率的前提下，上述两图的平均查找长度为：
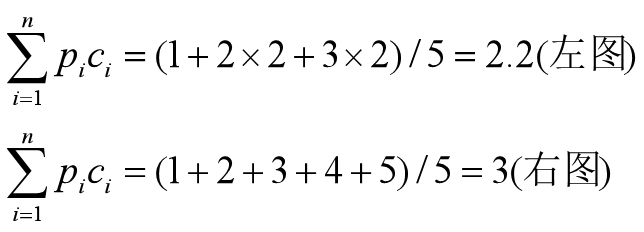
总结：
平均查找长度和二叉树的形态有关，即：
最好：log2n（形态匀称，与二分查找的判定树相似）
最坏: （n+1)/2（单支树）
（5）二叉排序树的操作——删除
将因删除结点而断开的二叉链表重新链接起来，并且尽可能地防止重新链接后树的高度增加。
删除叶结点：只需将其双亲结点指向它的指针清零，再释放它即可。
被删结点缺右子树：可以拿它的左子女结点顶替它的位置，再释放它。
被删结点缺左子树：可以拿它的右子女结点顶替它的位置，再释放它。
被删结点左、右子树都存在：可以在它的右子树中寻找中序下的第一个结点(关键码最小),或者左子树中寻址中序下的最后一个结点（关键码最大），用它的值填补到被删结点中，再来处理这个结点的删除问题。
