DLX (舞蹈链) 从入门到入土

DLX 从入门到入土

一 · 浅谈精确覆盖问题

精确覆盖问题（Exact Cover Problem），是指给定很多集合 $ S_i(1 \le i \le n) $

以及一个集合$ X $

求满足以下的无序多元组\((T_1,T_2,...,T_m)\)：

  1. \[\forall i,j \in [1,m],T_i \cap T_j = \varnothing (i \ne j) \]

  2. \[X = \bigcup_{i=1}^m T_i \]

  3. \[\forall i \in [1,m],T_i \in \{S_1,S_2,...,S_n\} \]

但是我们看不懂qwq（逃~

所以可以简化题意，假设有一个矩阵：

\[\begin{pmatrix} 0&0&1&0&1&1&0 \\ 1&0&0&1&0&0&1 \\ 0&1&1&0&0&1&0 \\ 1&0&0&1&0&0&0 \\ 0&1&0&0&0&0&1 \\ 0&0&0&1&1&0&1 \end{pmatrix} \]

你需要选择一些行，使这些行每一列有且仅有\(1\)个一。

如一组合法的解$ (1,4,5) $。

二 · 暴力

对于精确覆盖问题，一种常见的暴力为 $ O(mn \cdot 2^{n}) $ 因为每行有选或不选两种状态，检查时间为 $ O(mn) $ 。

经过异或位运算理论上可压缩至$ O(n \cdot 2^n) $，这里不作介绍。

三 · X算法

X 算法（由Donald E. Knuth发明），其思想与刚才的暴力差不多，但是方便优化。

定义：相关联指的是两行之间有\(1\)处于相同列。

以上面矩阵为例：

  1. 首先选择第一行，与之相关联的行与列全部删去。

    \[\begin{pmatrix} \color{blue}0&\color{blue}0&\color{blue}1&\color{blue}0&\color{blue}1&\color{blue}1&\color{blue}0 \\ 1&0&\color{blue}0&1&\color{blue}0&\color{blue}0&1 \\ \color{blue}0&\color{blue}1&\color{blue}1&\color{blue}0&\color{blue}0&\color{blue}1&\color{blue}0 \\ 1&0&\color{blue}0&1&\color{blue}0&\color{blue}0&0 \\ 0&1&\color{blue}0&0&\color{blue}0&\color{blue}0&1 \\ \color{blue}0&\color{blue}0&\color{blue}0&\color{blue}1&\color{blue}1&\color{blue}0&\color{blue}1 \end{pmatrix} \]

    得到一个更小的矩阵：

    \[\begin{pmatrix} 1&0&1&1 \\ 1&0&1&0 \\ 0&1&0&1 \end{pmatrix} \]

  2. 再次选择第一行，执行相同操作。

    \[\begin{pmatrix} \color{blue}1&\color{blue}0&\color{blue}1&\color{blue}1 \\ \color{blue}1&\color{blue}0&\color{blue}1&\color{blue}0 \\ \color{blue}0&\color{blue}1&\color{blue}0&\color{blue}1 \end{pmatrix} \]

  3. 删去后矩阵为空，但第一行\((1,0,1,1)\)不全为\(1\)，说明有一列并没有覆盖。

  4. 于是回溯至步骤2，选择第二行

    \[\begin{pmatrix} \color{blue}1&\color{blue}0&\color{blue}1&\color{blue}1 \\ \color{blue}1&\color{blue}0&\color{blue}1&\color{blue}0 \\ \color{blue}0&1&\color{blue}0&1 \end{pmatrix} \]

    余下：

    \[\begin{pmatrix} 1&1 \end{pmatrix} \]

  5. 此时选择第一行，删除后矩阵为空，且删去的全为\(1\)，选法合适。

    注意此时选择的行分别为\((1,4,5)\)。

算法毕。

四 · Dancing Links优化过的X算法

不难看出，X 算法需要大量的「删除行」、「删除列」和「恢复行」、「恢复列」的操作。

一个朴素的想法是，使用一个二维数组存放矩阵，再用四个数组分别存放每一行与之相邻的行编号，每次删除和恢复仅需更新四个数组中的元素。但由于一般问题的矩阵中 0 的数量远多于 1 的数量，这样做的空间复杂度难以接受。

于是Knuth先生想到了使用双向十字链表维护这个操作。

链表见过吗？

那么双向十字链表是这样的（可以感性理解为二维循环链表：

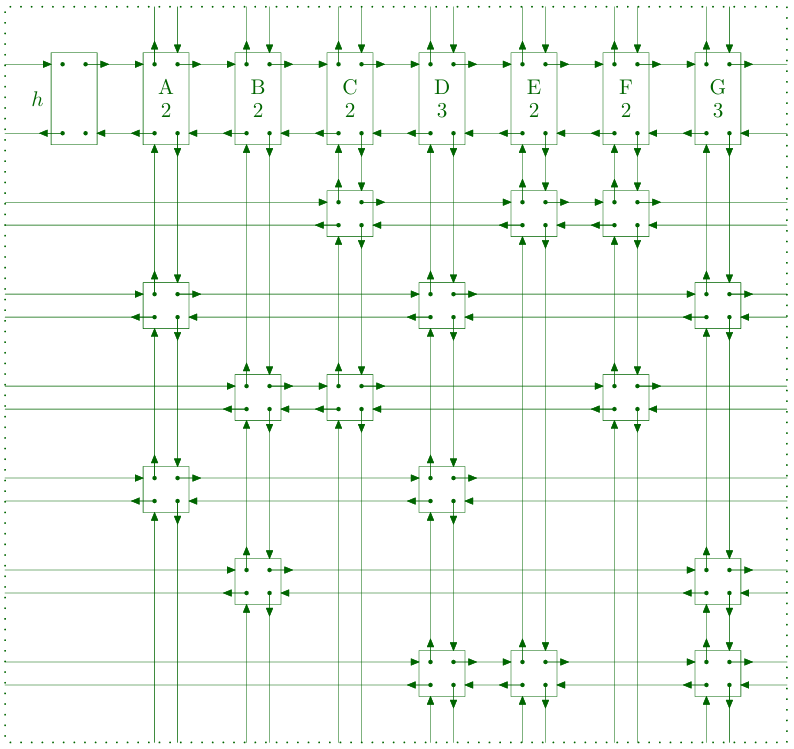
\(2025.6.2\)补注：矩形代表节点，线条代表指针，双向十字链表，顾名思义，一个节点有四个指针。

好的，现在我们就可以上代码了。

i.build函数
inline void build(int c) {
	for (int i = 0; i <= c; i++) {
		L[i] = i - 1, R[i] = i + 1;
		U[i] = i, D[i] = i;
	}
	L[0] = c, R[c] = 0, id = c + 1;
}

解释：首先将每一列都建立一个链头，（注意有一个\(0\)号节点），建立循环链表结构，\(L,R,U,D\)代表\(i\)节点左、右、上、下四个节点，\(id\)为后续节点的时间戳。

ii.remove函数
inline void remove(int x) {
	R[L[x]] = R[x], L[R[x]] = L[x];
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = U[z], D[U[z]] = D[z];
			colcnt[col[z]]--;
		}
	}
}

\(remove\)函数：移除一整列及其相关的行，通过双向十字链表进行链表基本删除操作。

\(colcnt\)数组，记录每一列\(1\)的个数。

iii.recover函数
inline void recover(int x) {
	R[L[x]] = x, L[R[x]] = x;
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = z, D[U[z]] = z;
			colcnt[col[z]]++;
		}
	}
}

没什么好讲的，\(remove\)函数逆操作。

iv.insert函数
inline void insert(int r, int c) {
	id++;//时间戳
	row[id] = r, col[id] = c;//row记录一个点的行，col为列
	colcnt[c]++;
	U[id] = c, D[id] = D[c], U[D[c]] = id, D[c] = id;
	if (!first[r]) first[r] = L[id] = R[id] = id;//first代表一行的链头
	else {
		L[id] = first[r], R[id] = R[first[r]];
		L[R[first[r]]] = id, R[first[r]] = id;
	}
}

就\(insert\)啊，插入。。。

v.dance函数

杀人魔法。

inline bool dance(int depth) {
	if (!R[0]) {
		ans = depth;//选择行总数
		//for (int i = 0; i < depth; i++) cout << rec[i] << ' ';输出方案
		return 1;
	}
	int y = R[0];
	for (int i = R[0]; i; i = R[i]) {
		if (colcnt[i] < colcnt[y]) y = i;
	}
	remove(y);
	for (int i = D[y]; i != y; i = D[i]) {
		rec[depth] = row[i];
		for (int j = R[i]; j != i; j = R[j]) remove(col[j]);
		if (dance(depth + 1)) return 1;
		for (int j = L[i]; j != i; j = L[j]) recover(col[j]);
	}
	recover(y);
	return 0;
}

认真解释：

  1. \(if(!R[0])\)段：若\(0\)号节点指向自己，说明矩阵已经清空，输出方案。
  2. 下面的\(for\)循环：此处与上文记载略不同，选择了\(1\)个数最多的一列进行操作，这是为了使程序有启发性，使递归次数更少，也就是速度更快 。
  3. 选择一行，执行删除相关联列的操作\(dance(dapth+1)\)
  4. 回溯

五 · 洛谷P4929 【模板】舞蹈链（DLX）模板代码

#include<bits/stdc++.h>
using namespace std;
const int N = 5505;
int n, m, id, ans;
int L[N], R[N], U[N], D[N], first[N], rec[N];
int colcnt[N], col[N], row[N];
inline void build(int c) {
	for (int i = 0; i <= c; i++) {
		L[i] = i - 1, R[i] = i + 1;
		U[i] = i, D[i] = i;
	}
	L[0] = c, R[c] = 0, id = c + 1;
}
inline void remove(int x) {
	R[L[x]] = R[x], L[R[x]] = L[x];
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = U[z], D[U[z]] = D[z];
			colcnt[col[z]]--;
		}
	}
}
inline void recover(int x) {
	R[L[x]] = x, L[R[x]] = x;
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = z, D[U[z]] = z;
			colcnt[col[z]]++;
		}
	}
}
inline void insert(int r, int c) {
	id++;
	row[id] = r, col[id] = c;
	colcnt[c]++;
	U[id] = c, D[id] = D[c], U[D[c]] = id, D[c] = id;
	if (!first[r]) first[r] = L[id] = R[id] = id;
	else {
		L[id] = first[r], R[id] = R[first[r]];
		L[R[first[r]]] = id, R[first[r]] = id;
	}
}
inline bool dance(int depth) {
	if (!R[0]) {
		ans = depth;
		for (int i = 0; i < depth; i++) cout << rec[i] << ' ';
		return 1;
	}
	int y = R[0];
	for (int i = R[0]; i; i = R[i]) {
		if (colcnt[i] < colcnt[y]) y = i;
	}
	remove(y);
	for (int i = D[y]; i != y; i = D[i]) {
		rec[depth] = row[i];
		for (int j = R[i]; j != i; j = R[j]) remove(col[j]);
		if (dance(depth + 1)) return 1;
		for (int j = L[i]; j != i; j = L[j]) recover(col[j]);
	}
	recover(y);
	return 0;
}
int main() {
	cin >> n >> m;
	build(m);
	int inp;
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= m; j++) {
			cin >> inp;
			if (inp) insert(i, j);
		}
	}
	if (!dance(0)) cout << "No Solution!";
	return 0;
}

一些 $ Q & A $

  1. 此处解释可以配合上文第四章食用哦｡:.ﾟヽ(*´∀`)ﾉﾟ.:｡

  2. \(Q\)：每一行的行头为\(first\)，那列头是什么？

    \(A\)：注意到\(build\)函数中，每列链头编号就是列数哦，如第\(4\)列链头为\(4\)。

  3. \(Q\)：为什么删除操作时同一列点上下不用断开，同一行左右不用断开？

    \(A\)：因为相关联的行列一定会同时被删，所以不用断开，方便维护

  4. \(2025.6.2\)补注：最近有 \(56\)~\(58\) 行顺序的问题，遂挖坑。

  5. 会有新的 $ Q & A $ 哦

六 · 变形——数独 SP1110 & UVA1309

网上很多博客其实并没有讲清楚数独的构建，遂在此留下做法。

DLX的建模方式，行表示被选择的元素，列选择限制的元素。

这样就可以保证受限元素只选一次啦~

具体地，数独建模有以下限制：

  1. 每一列只能有一个该数字
  2. 每一行只能有一个该数字
  3. 每一宫只能有一个该数字
  4. 每一个位置只能有一个数字

设一个位置的状态为 $ (i,j,k) $ ，$ (i,j) $ 为坐标，\(k\) 为数字。

若该位置数字确定，插入行 $ (line,16(i-1)+j) $ ，$ (line,16(i-1)+256+k) $ ，$ (line,16(j-1)+512+k) $ ，$ (line,16(Q-1)+768+k) $

即 $ 1 \sim 256 $ 列限制位置，$ 257 \sim 512 $ 列限制行，$ 513 \sim 768 $ 限制列，$ 769 \sim 1024 $ 限制宫。

总计 \(1024\) 列。

行数，每一格最多 \(16\) 种状态 \(256 \times 16 = 4096\) 行。

每行四个限制，空间 \(O(10^4)\) 足够了。

#include<bits/stdc++.h>
const int N = 2e4 + 100, M = 17;
int n, m, id, line, t;
int L[N], R[N], U[N], D[N], first[N], rec[N];
int colcnt[N], col[N], row[N];
int ans[M][M];
inline void build(int c) {
	for (int i = 0; i <= c; i++) {
		L[i] = i - 1, R[i] = i + 1;
		U[i] = i, D[i] = i;
	}
	L[0] = c, R[c] = 0, id = c + 1;
}
inline void remove(int x) {
	R[L[x]] = R[x], L[R[x]] = L[x];
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = U[z], D[U[z]] = D[z];
			colcnt[col[z]]--;
		}
	}
}
inline void recover(int x) {
	R[L[x]] = x, L[R[x]] = x;
	for (int y = U[x]; y != x; y = U[y]) {
		for (int z = R[y]; z != y; z = R[z]) {
			U[D[z]] = z, D[U[z]] = z;
			colcnt[col[z]]++;
		}
	}
}
inline void insert(int r, int c) {
	id++;
	row[id] = r, col[id] = c;
	colcnt[c]++;
	U[id] = c, D[id] = D[c], U[D[c]] = id, D[c] = id;
	if (!first[r]) first[r] = L[id] = R[id] = id;
	else {
		L[id] = first[r], R[id] = R[first[r]];
		L[R[first[r]]] = id, R[first[r]] = id;
	}
}
inline bool dance(int depth) {
	if (!R[0]) {
		int pos, x, y, num;
		for (int i = 0; i < depth; i++) {
			pos = first[rec[i]];
			x = (col[pos] - 1) / 16 + 1;
			y = (col[pos] - 1) % 16 + 1;
			pos = R[pos];
			num = (col[pos] - 1) % 16 + 1;
			ans[x][y] = num;
		}
		return 1;
	}
	int y = R[0];
	for (int i = R[0]; i; i = R[i]) {
		if (colcnt[i] < colcnt[y]) y = i;
	}
	remove(y);
	for (int i = D[y]; i != y; i = D[i]) {
		rec[depth] = row[i];
		for (int j = R[i]; j != i; j = R[j]) remove(col[j]);
		if (dance(depth + 1)) return 1;
		for (int j = L[i]; j != i; j = L[j]) recover(col[j]);
	}
	recover(y);
	return 0;
}
inline void init() {
	memset(L, 0, sizeof(L));
	memset(R, 0, sizeof(R));
	memset(U, 0, sizeof(U));
	memset(D, 0, sizeof(D));
	memset(first, 0, sizeof(first));
	memset(rec, 0, sizeof(rec));
	memset(colcnt, 0, sizeof(colcnt));
	memset(col, 0, sizeof(col));
	memset(row, 0, sizeof(row));
	memset(ans, 0, sizeof(ans));
	id = line = 0;
}
char inp;
int main() {
	cin >> t;
	while (t--) {
		init();
		build(1024);
		for (int i = 1; i <= 16; i++) {
			for (int j = 1; j <= 16; j++) {
				cin >> inp;
				int Q = (i - 1) / 4 * 4 + (j - 1) / 4 + 1;
				if (inp == '-') {
					for (int k = 1; k <= 16; k++) {
						line++;
						insert(line, (i - 1) * 16 + j);
						insert(line, (i - 1) * 16 + 256 + k);
						insert(line, (j - 1) * 16 + 512 + k);
						insert(line, (Q - 1) * 16 + 768 + k);
					}
					continue;
				}
				int x = inp - 'A' + 1;
				line++;
				insert(line, (i - 1) * 16 + j);
				insert(line, (i - 1) * 16 + 256 + x);
				insert(line, (j - 1) * 16 + 512 + x);
				insert(line, (Q - 1) * 16 + 768 + x);
			}
		}
		dance(0);
		for (int i = 1; i <= 16; i++) {
			for (int j = 1; j <= 16; j++) {
				cout << char(ans[i][j] + 'A' - 1);
			}
			cout << '\n';
		}
		cout << '\n';
	}
	return 0;
}
posted @ 2025-02-14 10:15  OrangeRED  阅读(18)  评论(1)    收藏  举报