CQOI2018day1 (XJOI contest908)
一题
破解D-H协议


时间限制:1S
内存限制:512M
具体思路:BSGS,没了
AC代码
#include<bits/stdc++.h> using namespace std; #define int long long int n,i,j,p,g,a,b,A,B; map<int,pair<int,int> > mp; int qpow(int a,int b) { int ans=1; while(b) { if(b%2)ans=ans*a%p; b=b/2;a=a*a%p; } return ans; } main() { // freopen("A.in","r",stdin); // freopen("A.out","w",stdout); scanf("%lld%lld",&g,&p); scanf("%lld",&n); int m=100000; for(i=0;i<=m;i++)mp[qpow(g,i)]=make_pair(1,i); while(n--) { scanf("%lld%lld",&a,&b); for(i=0;i<=m;i++) { int now=i*m; if(mp[qpow(qpow(g,now),p-2)*a%p].first) { A=now+mp[qpow(qpow(g,now),p-2)*a%p].second; break; } } for(i=0;i<=m;i++) { int now=i*m; if(mp[qpow(qpow(g,now),p-2)*b%p].first) { B=now+mp[qpow(qpow(g,now),p-2)*b%p].second; break; } } printf("%lld\n",qpow(qpow(g,B),A)%p); } return 0; }
第二题
社交网络
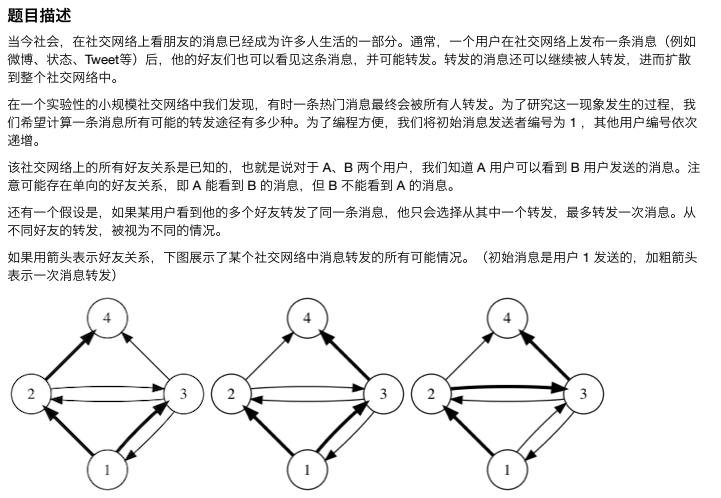
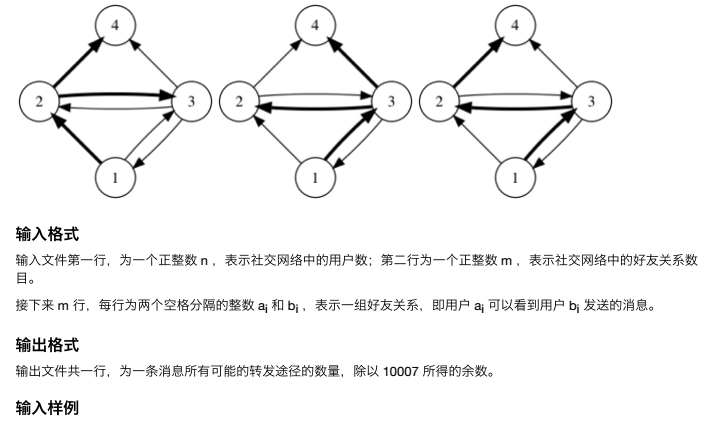
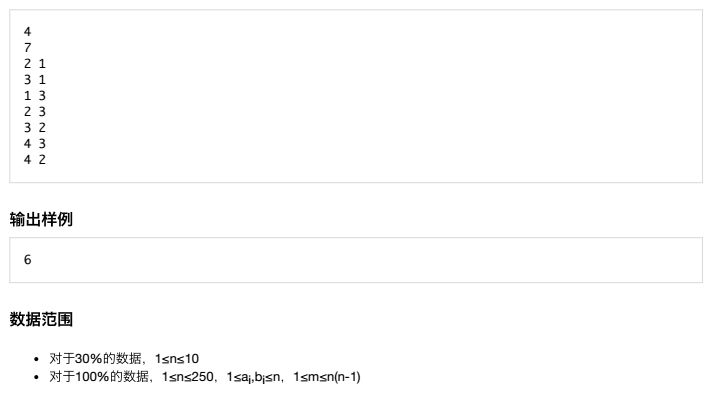
时间限制:1S
内存限制:512M
具体思路:矩阵树定理
先搞出基尔霍夫矩阵,然后去掉第一行列,然后高斯消元求行列式即可
AC代码
#include<bits/stdc++.h> #define int long long using namespace std; int n,m,i,j,a[500000],b[500000],k; int f[300][300]; const int ha=10007; int qpow(int a,int b) { int ans=1; while(b) { if(b%2)ans=ans*a%ha; b=b/2;a=a*a%ha; } return ans; } int gauss() { int ans=0; for(i=1;i<=n;i++) { int mx=i; for(j=i+1;j<=n;j++)if(f[j][i]>f[mx][i])mx=j; if(mx!=i) { ans^=1; for(j=1;j<=n;j++) swap(f[i][j],f[mx][j]); } if(f[i][i]==0) { f[1][1]=0; return 0; } for (j=i+1;j<=n;j++) if(f[j][i]!=0) { int now=f[j][i]*qpow(f[i][i],ha-2)%ha; for (k=i;k<=n;k++)f[j][k]=(f[j][k]-now*f[i][k]%ha+ha*ha)%ha; } } return ans; } main() { scanf("%lld%lld",&n,&m); for(i=1;i<=m;i++) { scanf("%lld%lld",&a[i],&b[i]); if(a[i]==1)a[i]=n;else if(a[i]==n)a[i]=1; if(b[i]==n)b[i]=1;else if(b[i]==1)b[i]=n; f[a[i]][b[i]]-=1;f[a[i]][b[i]]=(f[a[i]][b[i]]+ha)%ha; f[a[i]][a[i]]+=1;f[a[i]][a[i]]=(f[a[i]][a[i]]+ha)%ha; } n--; int ans=gauss()?(ha-1):1; for(i=1;i<=n;i++)ans=ans*f[i][i]%ha; printf("%lld",ans); return 0; }
第三题
交错序列


时间限制:1S
内存限制:512M
具体思路:O(n)枚举,然后组合数乱搞就过了
AC代码
#pragma GCC optimize(3) #pragma GCC target("avx") #pragma GCC optimize("Ofast") #pragma GCC optimize("inline") #pragma GCC optimize("-fgcse") #pragma GCC optimize("-fgcse-lm") #pragma GCC optimize("-fipa-sra") #pragma GCC optimize("-ftree-pre") #pragma GCC optimize("-ftree-vrp") #pragma GCC optimize("-fpeephole2") #pragma GCC optimize("-ffast-math") #pragma GCC optimize("-fsched-spec") #pragma GCC optimize("unroll-loops") #pragma GCC optimize("-falign-jumps") #pragma GCC optimize("-falign-loops") #pragma GCC optimize("-falign-labels") #pragma GCC optimize("-fdevirtualize") #pragma GCC optimize("-fcaller-saves") #pragma GCC optimize("-fcrossjumping") #pragma GCC optimize("-fthread-jumps") #pragma GCC optimize("-funroll-loops") #pragma GCC optimize("-fwhole-program") #pragma GCC optimize("-freorder-blocks") #pragma GCC optimize("-fschedule-insns") #pragma GCC optimize("inline-functions") #pragma GCC optimize("-ftree-tail-merge") #pragma GCC optimize("-fschedule-insns2") #pragma GCC optimize("-fstrict-aliasing") #pragma GCC optimize("-fstrict-overflow") #pragma GCC optimize("-falign-functions") #pragma GCC optimize("-fcse-skip-blocks") #pragma GCC optimize("-fcse-follow-jumps") #pragma GCC optimize("-fsched-interblock") #pragma GCC optimize("-fpartial-inlining") #pragma GCC optimize("no-stack-protector") #pragma GCC optimize("-freorder-functions") #pragma GCC optimize("-findirect-inlining") #pragma GCC optimize("-fhoist-adjacent-loads") #pragma GCC optimize("-frerun-cse-after-loop") #pragma GCC optimize("inline-small-functions") #pragma GCC optimize("-finline-small-functions") #pragma GCC optimize("-ftree-switch-conversion") #pragma GCC optimize("-foptimize-sibling-calls") #pragma GCC optimize("-fexpensive-optimizations") #pragma GCC optimize("-funsafe-loop-optimizations") #pragma GCC optimize("inline-functions-called-once") #pragma GCC optimize("-fdelete-null-pointer-checks") #include<bits/stdc++.h> using namespace std; #define int long long int tot,n,m,i,j,A[10001000], B[10001000],inv[10000010],factinv[10000010],fact[10000010],pri[1001000],mod; bool np[10001000]; int a,b,ans; int qpow(int a,int b) { int ans=1; while(b) { if(b%2)ans=ans*a%mod; b=b/2; a=a*a%mod; } return ans; } int C(int x,int y) { return fact[x]*factinv[y]%mod*factinv[x-y]%mod; } main() { scanf("%lld%lld%lld%lld",&n,&a,&b,&mod); m=min(n+1,mod-1); inv[1]=1;factinv[1]=1;fact[1]=1;inv[0]=1; for(i=2; i<=m; i++)fact[i]=fact[i-1]*i%mod; factinv[m]=qpow(fact[m],mod-2); for (i=m;i>0;--i) factinv[i-1]=factinv[i]*i%mod; A[0]=!a;B[0]=!b;A[1]=B[1]=1; for (i=2; i<=n; ++i) { if (!np[i]) { A[i]=qpow(i,a); B[i]=qpow(i,b); pri[++tot]=i; } for (j=1; j<=tot&&pri[j]*i<=n; ++j) { np[pri[j]*i]=1; A[pri[j]*i]=A[i]*A[pri[j]]%mod; B[pri[j]*i]=B[i]*B[pri[j]]%mod; if (i%pri[j]==0) break; } } for(i=0; i<=(n+1)/2; i++) ans+=C(n-i+1,i) *A[n-i]%mod *B[i]%mod; printf("%lld",ans%mod); return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号