[数据结构] 几种排序算法(未完成)
1、插入排序
直接插入排序(Insertion Sort)的基本思想是:每次将一个待排序的元素,按其关键字大小插入到前面已经排好序的子序列中的适当位置,直到全部记录插入完成为止。
设数组为a[0…n-1]。
1. 初始时,a[0]自成1个有序区,无序区为a[1..n-1]。令i=1
2. 将a[i]并入当前的有序区a[0…i-1]中形成a[0…i]的有序区间。
3. i++并重复第二步直到i==n-1。排序完成。
2、希尔排序
希尔排序的实质就是分组插入排序。
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由序号相差某个“增量”的元素组成的),分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的。
一般我们进行希尔排序时,会取增量gap=数组长度/2,每完成一次这个gap下分组的直接插入排序后,将gap再次除以2得到新的gap。例子如下:
{ 49,38,65,97,26,13,27,49,55,4 },这是一个长度n=10的数组,我们对它进行从小到大的排序
① gap = 10/2 = 5,

1A,1B为一组,2A,2B为一组......我们将数据分成了五组:{ 49,13 },{ 38,27 },{ 65,49 },{ 97,55 },{ 26,4 }。我们对这五组数据分别进行插入排序,得到了{ 13,49 },{ 27,48 },{ 49,65 },{ 55,97 },{ 4,26 },放回原来的数组,我们开始第二次:
② gap = 5/2 = 2,

我们得到了{ 13,49,4,38,97},{ 27,55,49,65,26 }。将这两组数据再一次进行插入排序我们得到 { 4,13,38,49,97 },{ 26,27,49,55,65 },保持他们在原数组中的位置,我们开始第三次:
③ gap = 2/2 = 1,

这一次我们得到 { 4,26,13,27,38,49,49,55,97,65 },再进行插入排序得到 { 4,13,26,27,38,49,49,55,65,97 },最后我们得到了完成排序的数组:
④ gap = 1/2 = 0:
![]() '
'
3、快速排序
快速排序的思路:
1.先从数列中取出一个数作为基准数。
2.分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。(或者小于等于的放到左边,大于的放到右边)。
3.再对左右区间重复第二步,直到各区间只有一个数。‘
我们举个例子:
以下面这个数组为例

我们需要设置 i = 0,j = 9,也就是分别指向这个数组的最左和最右侧。以a[0]为基准,我们将a[0]的72作为参考值。
我们从右侧开始,85,48!48就是小于72的值,于是我们交换 48 和 72 的位置。此时 i = 0, j = 8。

然后从左侧开始,找到6,57,88!88是大于72的值。我们再一次交换88和72的位置。此时 i = 3,j = 8 。

重复如此,直到 i == j。此时72左边区域的所有元素都比72要小,右边区域的所有元素都比72要大。

此时,我们使用递归的方式。将72左侧和右侧的区域再次使用上述的方法来进行排序。最终我们会得到完整的从小到大排列的这个数组。
4、堆排序
堆,是一种二叉树,他满足每个结点的值都大于等于(或小于等于)它的左右孩子的结点的值。
二叉树是可以用一个数组来表示的,详见二叉树的相关实现知识。
堆排序的思路:
a.将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆;
b.将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端;
c.重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
堆排序的例子:(这个例子中我们最后实现由小到大排序)
1.我们得到了一组需要排序的数据,用数组存放。此时可以把它看做一个无序的二叉树:
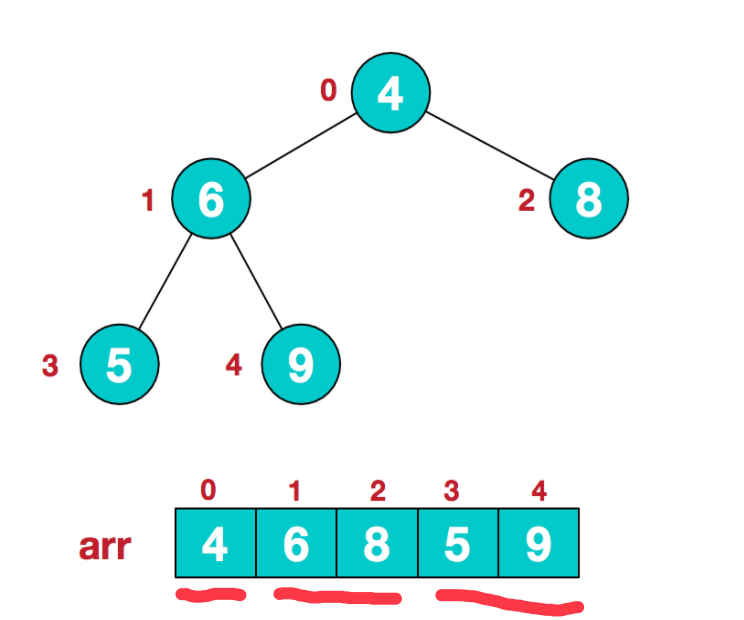
2.我们需要把这棵二叉树调整为一个最大堆(没有打错,就是最大堆,后面会处理)。我们从最后一个非叶子结点开始处理。若果数据长度为L,那么最后一个非叶子节点的下标是[L/2]-1,在这个例子中就是 5/2 - 1 = 2 -1 = 1,也就是数据6所在的结点。调整以这个结点为根节点的子树,调整这棵子树,让它满足根节点大于它的左右孩子。继续找到倒数第二个非叶子结点。做同样的处理,然后倒数第三个,第四个......
3.处理完毕之后,我们得到了一个最大堆。此时他的堆结构和数组表示是这样的:
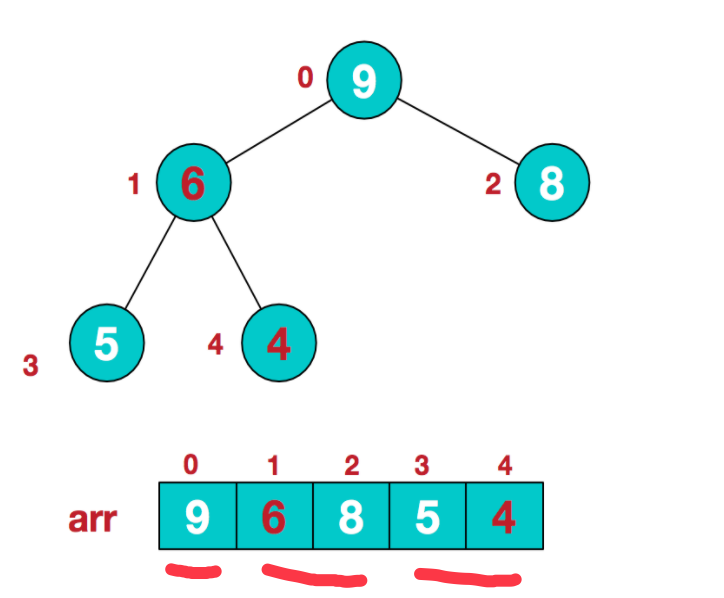
4.此时堆顶部的元素是最大的。将堆顶部的元素与末位的元素交换位置,得到新的数据结构:
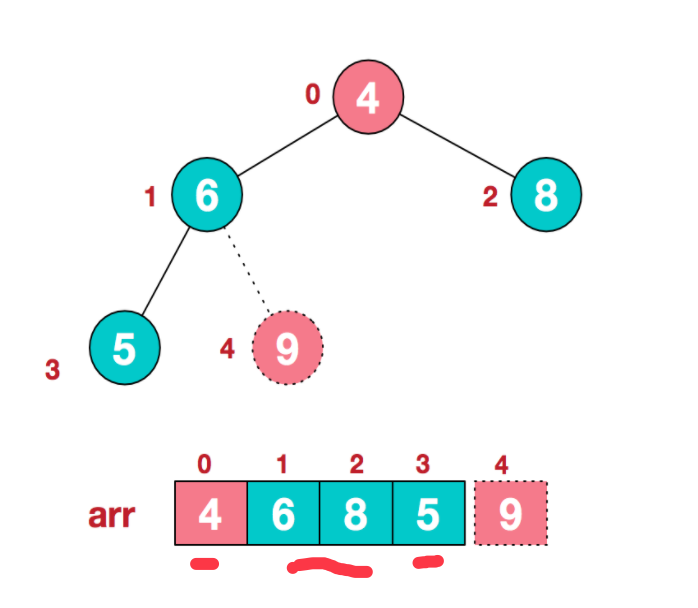
5.交换之后,将当前处于末位的元素(原最大元素)排除在堆结构之外,对剩下的元素构成的堆进行调整,让它依然满足最大堆的结构。

6. 重复4,5两步,直到堆结构为空。我们得到了如下的数据构造。此时数组中的元素已经按从小到大的顺序排列了。

二路归并排序
基数排序
排序算法间的比较
未完。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号