[数据结构] 图 ,邻接矩阵法,邻接表法
图
一个图,由顶点(vertex)集和边(edge)集E组成。每一条边,连接了两个顶点,也就是一个点对。
有向图 无向图
如果点对之后是分次序的(比如仅限于从A点到B点),那么这这个图就是有向图(digraph)。此时我们可以把边叫做弧(arc)。
如果没有次序的差别,那么就是无向图。

图-无向图和有向图
连通 强连通 弱连通
在上图的无向图中,由B到A,可以走B→A,也可以走B→C→A,还可以走B→C→D→A。
在上图的有向图中,由B到A,因为受到次序的限制,只能走B→A,B→C→A。
对于这样的线路,除了出发的顶点和结束的顶点之外,要求经过的顶点都不相同。这样这样的一组顶点序列就叫做一条路径。
对于无向图,如果任意两个顶点都能找到一条路径,这个无向图就是连通的。
对于有向图,在弧方向的限制下,如果任意两个顶点都能找到一条路径,这个有向图就是强连通的。如果去掉弧的指向才能满足条件,那么就是弱连通的。
完全图
当一个图中,每一个点和任意另一个点之间都是点对(都由边连接),这个图就是完全图。

图-完全图
图的现实应用举例
图的现实应用还是非常好理解的。
在城市里坐地铁,地铁线路图就是一个 图 。从 下沙江滨站 ,要前往 龙翔桥站 ,就是在找这两个顶点间的路径。
图的实现方法
仍然使用C语言举例。
邻接矩阵法
邻接矩阵法:用一个一维数组来保存顶点的信息,用一个二维数组来保存与 边 相关的信息。
比如下面这个无向图的例子,我们用0表示两个顶点间没有边,1表示这两个顶点间的边存在:

图-邻接矩阵法的简单示例(无向图)
其实二维数组中还可以存储更多的内容,比如在上面地铁的例子中,可以在二维数组中存储两个顶点的距离,然后用-1表示这两个顶点间无可通地铁路径。具体的使用方式,存储的内容都可以参照实际的需求进行变更。
我们再看一下有向图的例子。这一次,我们为每一条边都加入一个权,这个权的实际意义,比如两个顶点间的地铁的距离。用无穷远表示两个顶点之间没有有效的边。

图-邻接矩阵法的例子(带 权 的有向图)
需要注意的是:邻接矩阵对于边数相对顶点较少的图,就是对存储空间极大的浪费。
邻接表
对于边的数目相对于顶点较少的图,使用邻接表。
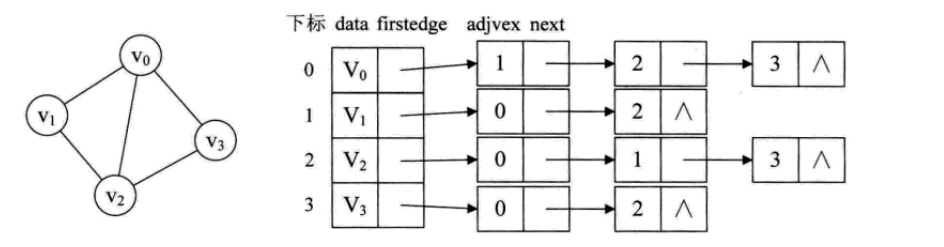
图-无向图的邻接表法
以C语言为例,构造一个无向图的邻接表。我们需要两种结构体。构造 结构体A 来表示一个顶点。data部分存放该顶点的数据,firstedge是指针。
再构造一个结构体B,adjvex来表示顶点的下标或地址,next表示下一个顶点的地址。
现在我们用一个结构体A的数组,来装下所有顶点的数据。再以V0这个顶点为例。V0与V1,V2,V3邻接。我们将V0所在的结构体A的firstedge指向一个结构体B1,这个结构体B1的adjvex存放的是V1的地址下标“1”,让它的next再指向下一个结构体B2,这个结构体B2中的adjvex存放的是V2的地址下标2,它的next再指向第三个结构体B3,这个结构体中存放V3的地址下标“3”。此时,V0所邻接的所有顶点都已经被连接在一起了。所以第三个结构体B的next为空。比较容易觉得奇怪的地方是,V0和这三个顶点的连接其实是没有顺序之分的,但在这个表达方式中,似乎给了人一种他们有次序的错觉。实际上他也只是把与V0邻接的所有顶点串在一起而已,连接的次序没有实际意义。
有向图也可以用邻接表法,但是由于有向图的弧的方向性,我们需要用两个邻接表来表示一个有向图。一个邻接表,存放从这个顶点指向外部的弧形成的图,另外一个存放指向这个顶点的弧形成的图。比如下面这个例子:

图-有向图的邻接表
记录顶点指向外部的图时,叫做邻接表。记录指向该顶点的弧时,叫做逆邻接表。
未完。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号