[数据结构]二叉树
二叉树
二叉树(binary)是一种特殊的树。二叉树的每个节点最多只能有2个子节点。
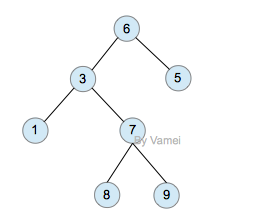
图-二叉树的结构示意/实现逻辑(这棵树只有展示用途,没有实际意义)
因为子节点的个数确定了,所以每一个节点只需要两个指针,一个指向当前节点的左子节点(left children),一个指向右子节点(right children)。
二叉搜索树(二叉查找树)
我们以二叉搜索树作为一个例子。
前文出现的树只作为展示示例,而并没有什么实际意义。
现在,我们考虑为二叉树的数据存放增加一个条件:每个节点都不比它左子树的任意元素小,而且不比它的右子树的任意元素大。
所谓左子树,就是把它的左子节点视为一个根节点之后,这个根节点下的树。右子树同理。
增加了上述这个条件后,我们就得到了 二叉搜索树。
我们对{ 6,3,5,1,8,7,9 }这组数据,选取“8”作为根节点(关键值),构造一个二叉搜索树:。
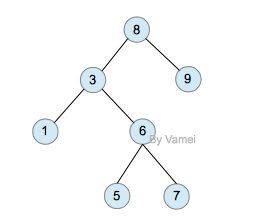
图-二叉搜索树
构造了这样的结构之后,我们可以更快的对数据进行搜索。我们按照以下逻辑对数据x进行查找:
1. 如果x等于根节点,那么找到x,停止搜索 (终止条件)
2. 如果x小于根节点,那么搜索左子树,回到第一步
3. 如果x大于根节点,那么搜索右子树,回到第一步
我们在进行搜索时,对二叉搜索树进行操作的最大次数就是这棵树的深度。
*在使用C语言构造搜索二叉树的过程中,你可能会发现“删除”操作异常麻烦。有一种简单的替代操作,称为懒惰删除(lazy deletion)。在懒惰删除时,我们并不真正从二叉搜索树中删除该节点,而是将该节点标记为“已删除”。这样,我们只用找到元素并标记,就可以完成删除元素了。如果有相同的元素重新插入,我们可以将该节点找到,并取消删除标记。。树所占据的内存空间不会因为删除节点而减小。懒惰节点实际上是用内存空间换取操作的简便性。
二叉树的遍历
中序遍历(Inorder Traversal):从根节点开始,先处理左子树,左子树所有元素处理完毕之后,再处理当前根节点,再处理右子树。
后序遍历(Postorder Traversal):从根节点开始,先处理左子树,左子树所有元素处理完毕之后,再处理右子树,右子树所有元素处理完毕之后,再处理当前根节点。
先序遍历(Preorder Traversal):从根节点开始,先处理当前根节点,然后处理左子树,左子树所有元素处理完毕之后,再处理右子树。
我们以 树 那篇随笔中的这棵表达式树为例:
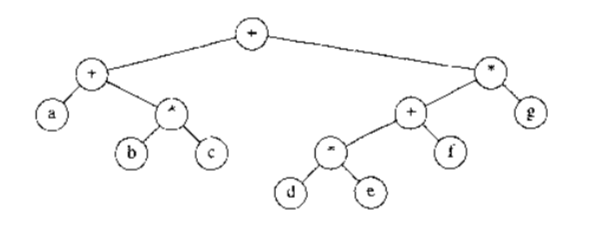
图-表达式树
中序遍历结果:(a+(b*c)) + ((d*e)+f)*g)
后序遍历结果:abc*+de*f+g*+
先序遍历结果:++a*bc*+*defg
AVL树
AVL树是最先发明的自平衡二叉查找树(Self-Balancing Binary Search Tree,简称平衡二叉树)。
AVL树是满足以下条件的树:
条件一:它必须是二叉查找树。
条件二:每个节点的左子树和右子树的高度差至多为1。
维持住条件二,可以保证AVL树的查找、插入、删除操作在平均和最坏的情况下,操作复杂度都是O(log n)。那么为了维持条件二,我们需要对AVL树进行动态的调整,在每一次数据改动之后,对节点进行调整使AVL树持续满足条件二。
如果我们使用C语言来构造一棵AVL树,那么在之前二叉树的基础上,一个节点中应当包含以下四个数据:
1、当前节点的数据;2、当前节点的高度;3、指向左子节点的指针;4、指向右子节点的指针。
每当对AVL树的节点进行操作之后,我们需要判断AVL树是否仍然维持平衡,也就是每个节点左右子树的高度差是否仍小于等于一。
比如,我们现在有一棵二叉树{4,5},我们需要向其中增加一个数据 6 。按照二叉搜索树的要求,我们会把它加入右子树的右节点,但此时对于根节点“4”来说,左子树高度为0,右子树高度为2,这棵AVL树很明显失衡了,所以我们需要对它进行调整。
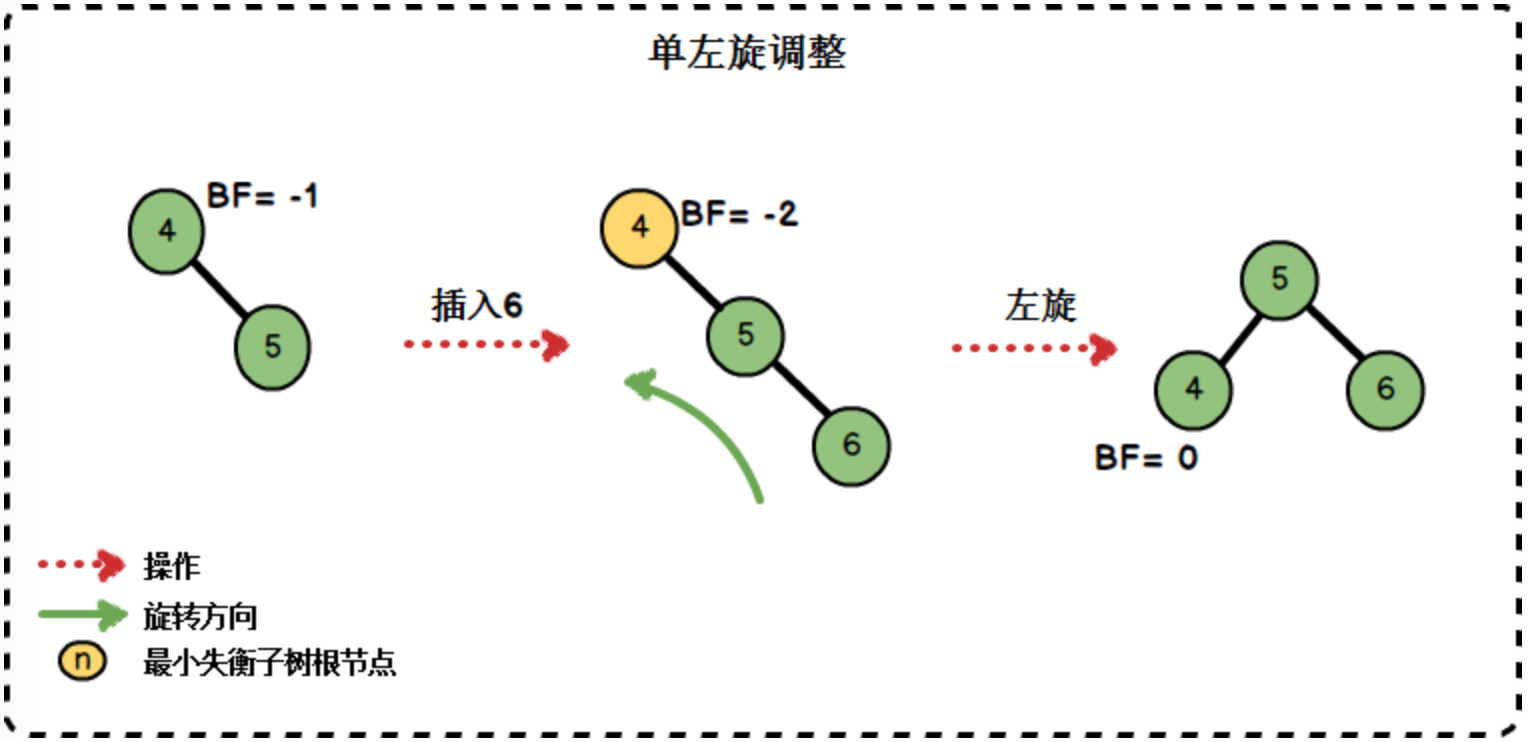
图-插入数据后失衡的AVL树的单左旋调整
还有以下操作下的若干调整方式:
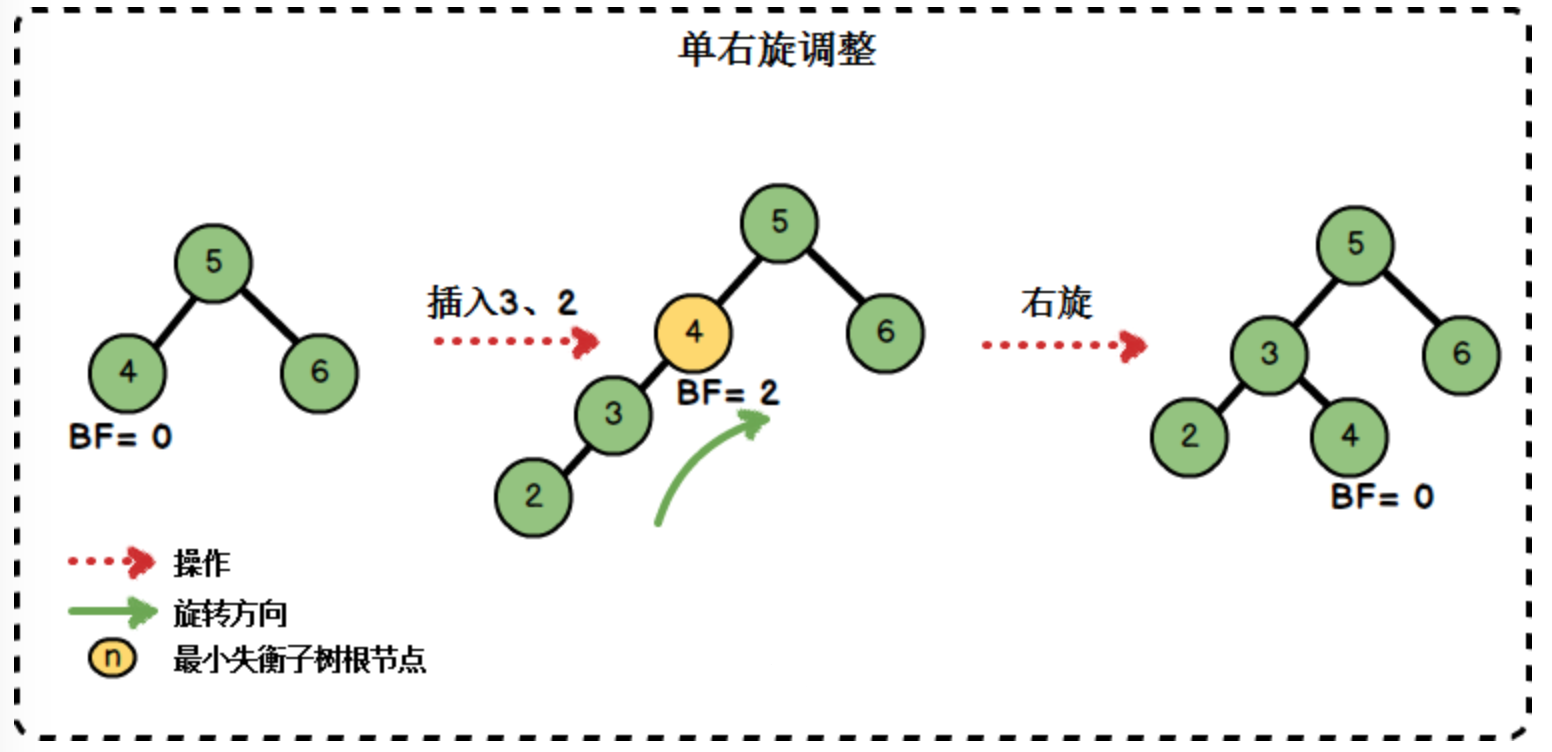
图-单右旋调整

图-先左旋后右旋调整
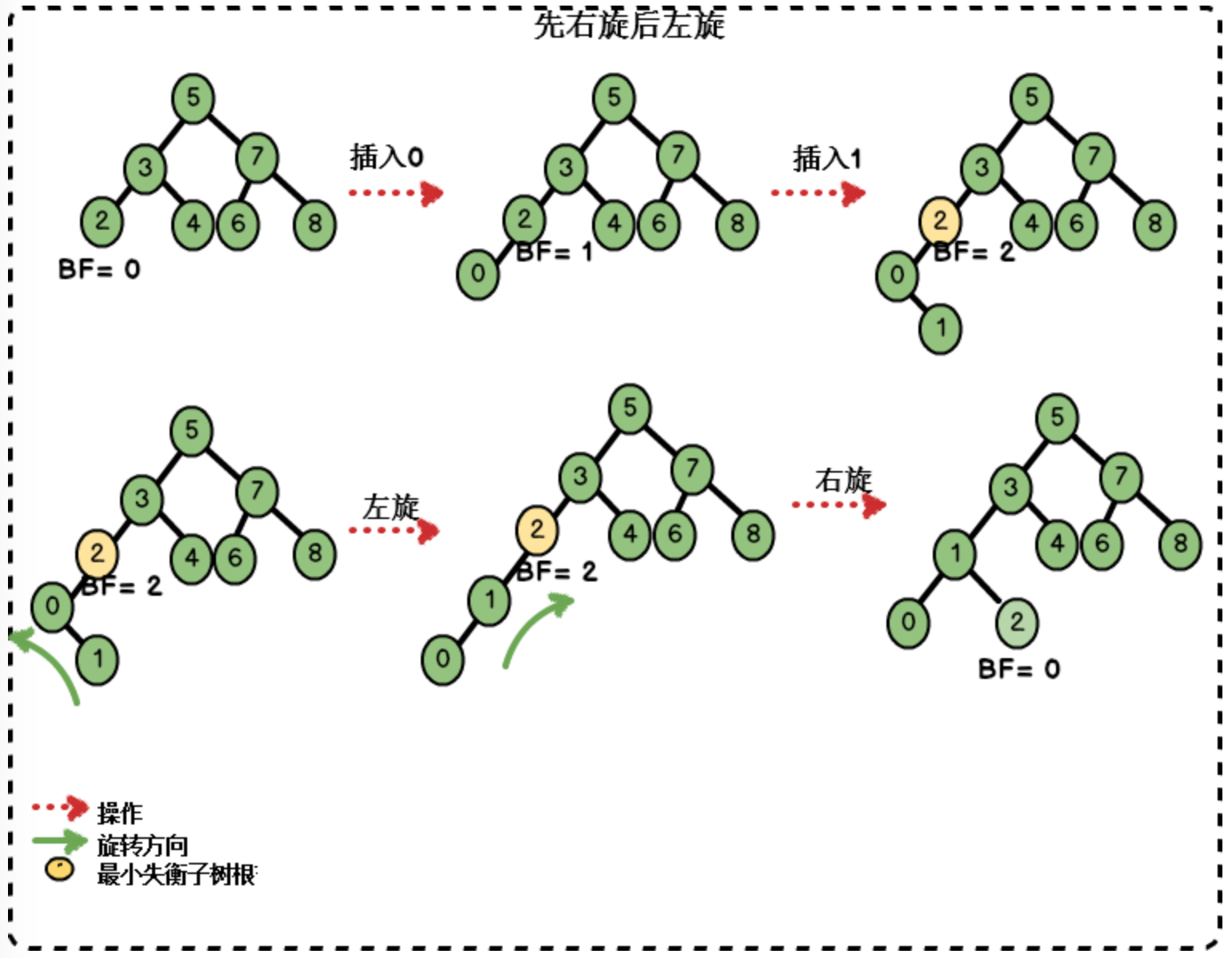
图-先右旋后左旋调整
其实可以发现,每种节点的加入方式都对应了一种调整方式,如下
| 类型 | 使用情形 |
|---|---|
| 单左旋 | 在左子树插入左孩子节点,使得平衡因子绝对值由1增至2 |
| 单右旋 | 在右子树插入右孩子节点,使得平衡因子绝对值由1增至2 |
| 先左旋后右旋 | 在左子树插入右孩子节点,使得平衡因子绝对值由1增至2 |
| 先右旋后左旋 | 在右子树插入左孩子节点,使得平衡因子绝对值由1增至2 |
删除节点也可能导致AVL树的失衡,实际上删除节点和插入节点是一种互逆的操作:
1、删除右子树的节点导致AVL树失衡时,相当于在左子树插入节点导致AVL树失衡。
2、删除左子树的节点导致AVL树失衡时,相当于在右子树插入节点导致AVL树失衡。



