【翻译】使用粒子群优化和引力搜索算法与神经网络的模糊混合在室内环境中进行用户定位

(User Localization in an Indoor Environment Using Fuzzy Hybrid of Partiocle Swarm Optimization & Gravitational Search Algorithm with Neural Networks)

Jayant G. Rohra1, Boominathan Perumal1(&),
Swathi Jamjala Narayanan1, Priya Thakur1, and Rajen B. Bhatt2

1 VIT Univerity, Vellore 632014, India jayant.rohra95@gmail.com, swathi.jns@gmail.com, boominathan.p@vit.ac.in, pthakur93@yahoo.com 2 Robert Bosch Research Labs, Pittsburgh, USA rajen.bhatt@gmail.com

摘要：基于 Wi-Fi 信号强度检测室内环境中的用户具有广泛的应用领域。这可用于在智能家居系统中定位用户、在有限区域中定位犯罪分子、获取接入点上的用户数量等目标。本文开发了一个优化模型，可部署在用于定位用户的监控和跟踪设备中基于他们在个人设备中接收到的 Wi-Fi 信号强度。在这里，我们从各种路由器获取信号强度数据，将它们映射到用户的位置，并将这种映射视为分类问题。我们使用由粒子群优化和引力搜索算法 (FPSOGSA) 提出的模糊混合获得的权重来训练神经网络，这是一种优化策略，可以提高模型的准确性。

关键词：神经网络 ⋅ 优化方法 ⋅ PSO ⋅ GSA ⋅ PSOGSA ⋅ 用户定位 ⋅ Wi-Fi 信号强度 ⋅ 模糊逻辑

1 引言

基于位置的服务的进步为移动计算带来了广阔的前景。已经采用了许多策略来为用户提供基于位置的定制服务。这些策略在电子商务收入、嵌入式智能系统、基于位置的推荐系统和其他各种领域都显示出巨大的繁荣。可以利用 GPS、蓝牙和 Wi-Fi 等技术来提供此类服务。布鲁苏等人。 [1] 使用 GPS 方法进行用户定位，但这些方法仅用于在特定范围内实现精度，并且由于卫星信号较弱，无法应用于室内位置。蓝牙是另一种可用于实现此目的的技术，但它只能很好地应用于短距离。因此，使用 Wi-Fi 接入点进行用户定位可能是一种更好的方法。萨拉查等人。引入了预测人们行为的方法 监控他们的日常活动。当人们需要必要的康复时，这种位置检测系统也可用于恐慌情况和灾难。阮等人。 [3] 为患有严重脑损伤的患者提出了识别技术，这些患者可以通过观察他们的运动模式来进行监测。裴等人。 [4] 提出了 SVM 技术，并显示出比其他现有学习技术更好的分类率。 Cho [5] 提出了使用智能手机的位置服务日志对室内和室外区域的位置进行分类的学习方法。邹等人。 [6] 介绍了一种基于极端机器学习策略的室内定位机制，并描述了它对多种环境的轻松适应。

Zadeh [7] 介绍了在实时控制器、诊断系统等许多领域广泛采用的模糊集理论。现实世界的数据具有各种维度，远远超过经典的真假逻辑。模糊逻辑用于关联现实生活场景，表示在 0 到 1 范围内测量真实程度的概率。Jang 和 Sun [8] 提出了用模糊逻辑和参数化控制建模神经网络的有趣概念。单独的神经模糊策略不足以获得神经网络的最佳吞吐量。我们的问题的需要在于使用更好的学习技术在正确的位置检测用户。但是大多数提出的技术都缺乏正确训练模型的优化策略的恰当使用。

我们研究了可以为优化策略提供足够好的解决方案的元启发式技术。 Eberhart 和 Kennedy [9] 引入了粒子群优化 (PSO) 策略，该策略考虑了一组候选解或粒子在搜索空间中移动，并使用它们的位置和速度参数更新为它们的 localBest 或 globalBest。标准 PSO 算法存在探索新搜索空间的能力等主要问题。 Shi 和 Russell [10] 介绍了一种自适应 PSO 方法，该方法使用多个基准函数来测试应用于 PSO 各个维度的模糊系统。 Liu 和 Abraham [11] 提出了一种模糊 PSO，通过在 PSO 的速度分量中引入湍流因子来强调探索新搜索空间的必要性。然而，这些算法缺乏获得全局最优的保证。米尔贾利利等人。 [12] 通过提出一种混合 PSOGSA 克服了这个问题，它引入了 GSA 逃避局部最优的能力，从而提高了神经网络的准确性。但是，当问题的维度增加时，该算法缺乏一致性并且在搜索的较低迭代中饱和。南迪等人。 [13] 提出了一种基于蜂群的反向传播方法来训练 ANN。因此，这些技术即兴发挥了这样一个事实，即基于 MLP 的分类器在使用优化方法进行训练时确实提供了良好的性能准确性。卡瓦姆等人。 [14] 使用布谷鸟群和 PSO 技术来训练 MLP，因此描述了使用优化策略的需要确实大大提高了神经网络的性能。但是，采用的各种此类技术往往缺乏适当的收敛性，无法保证探索完整的种群。

考虑到这些因素，我们提出了 FPSOGSA，它克服了将自身困在局部最小值中的可能性并提高了更高收敛速度的概率。在更高的迭代中，它会逐渐降低错误率而不是达到饱和，如 PSOGSA 所示。它获得了更好的收敛性，增强了优化神经网络的能力，从而降低了模糊神经网络（FNN）的均方误差。许多这样的方法已被用于训练各种分类器。人工神经网络 (ANN) 是一种易于理解和使用的模型。更重要的是，它本质上是非线性和非参数的。 ANN 主要用于解决各种问题。考虑到这些因素，我们提出了 FPSOGSA，它克服了自身陷入局部最小值的可能性并提高了更高收敛速度的概率。在更高的迭代中，它会逐渐降低错误率而不是达到饱和，如 PSOGSA 所示。它获得了更好的收敛性，增强了优化神经网络的能力，从而降低了模糊神经网络（FNN）的均方误差。许多这样的方法已被用于训练各种分类器。人工神经网络 (ANN) 是一种易于理解和使用的模型。更重要的是，它本质上是非线性和非参数的。 ANN 主要用于通过反向传播 (BP) 算法解决各种分类和预测问题。但是，BP 收敛速度较慢且无法保证。因此，我们需要使用优化策略来获得更快的收敛和更高的准确率。因此，我们在这里引入混合 PSOGSA 策略作为优化策略。另一方面，ANN 被认为是一种黑盒学习方法。它无法处理不确定性。为了克服这个问题，我们引入了模糊组件。 Fuzzy在处理不确定性方面相当出色，还可以通过产生规则来解释输入和输出之间的关系。因此，我们介绍 FPSOGSA 算法。

2 将用户定位作为一个分类问题

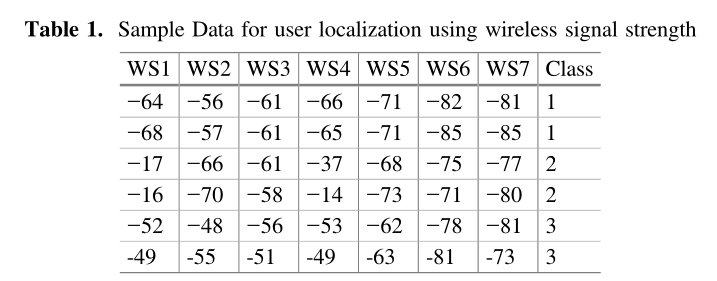
​ 为了准确预测用户的位置，必须在跟踪或监控设备中训练和部署明确且一致的模型。我们在有界位置测量从各种路由器接收到的 Wi-Fi 信号强度并训练神经网络，以便它可以进一步预测具有信号强度的未知元组集的用户位置。在这里，我们考虑在美国匹兹堡的办公地点进行设置。办公室有 7 个 Wi-Fi 路由器，从这些路由器接收到的信号强度对用户在会议室、厨房或室内运动室的位置进行分类。示例数据列表如表 1 所示。WS1 对应于从路由器 1 接收到的信号强度，WS2 对应于从路由器2 接收到的信号强度，对于其他路由器也是如此。与会议室、厨房和室内运动相对应的类别标签分别标记为 1、2 和 3。在我们的设置工具中，我们考虑了 Android 设备和设备捕获的无线信号强度列表。在某些位置，通过以恒定时间间隔（这里考虑每 1 秒）轮询无线信号强度来观察信号强度。这再次在其他位置重复，并为在该设施对七个不同路由器进行的一千五百次观察收集了合适的数据。因此，这里开发的模型可以根据有界位置的场景和物理设施中无线路由器的数量来重复使用。通过将七个无线路由器作为输入维度，该数据被公式化为模式分类数据集，这些输入维度用于预测用户在办公室中的位置，作为三个维度类别之一。在准备好具体的数据集之后，我们现在使用元启发式方法训练神经网络，该方法提高了对正确类标签进行最佳分类的机会。我们在 Sect 中讨论了使用模糊 PSO GSA (FPSOGSA) 训练模型的方法。

3 从传统 PSOGSA 到 FPSOGSA 的演变以及使用提出的 Fuzzy-PSOGSA 算法训练神经网络

​ Mirjalili 等人。 [12] 通过在标准 PSO 算法中引入一种利用能力来提高找到全局最佳解决方案的概率，从而提出了 PSOGSA。 Rashedi 等人提出的通过包含引力搜索能力来利用粒子间质量相互作用的新想法。 [15] 进一步提高了 FNN 的准确率。在本节后面，我们将介绍 PSOGSA 的模糊决策参数，这些参数决定了在搜索空间中进一步探索粒子的需要。设置合适的阈值来决定粒子是否需要探索更多维度。因此，该算法将满足不错过 globalBest 的需要，因为它为粒子提供了更多的探索能力。

​ 我们最初考虑一个具有“N”个粒子的空间，这些粒子具有随机分配的位置，这些位置被称为粒子的当前位置 (CurrPos)。这些粒子中的每一个的位置都具有“d”维，并且这些位置的配置被认为是候选解。每次迭代中粒子之间的力计算为，

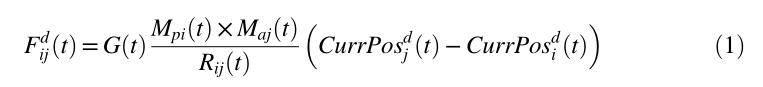
​ 其中 \(M_{pi}\) 和 \(M_{aj}\) 分别是粒子 i 和 j 的被动和主动引力质量，\(R_{ij}\) 被计算为两个粒子之间的欧几里得距离。作用在任何粒子 i 上的总力被计算为作用在空间中所有其他粒子上的力的总和。时变引力常数 \(G(t)\) 计算为：

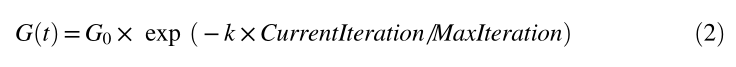
其中 k 是递减系数，G0 是 t 处的初始引力常数值。每个粒子的质量与适应度值有关。它使用等式在每个时期更新，

其中 best 是最小化优化问题的最小适应度值，最差是最大适应度值。粒子的加速度计算如下：

权重函数 W 使用以下公式计算：

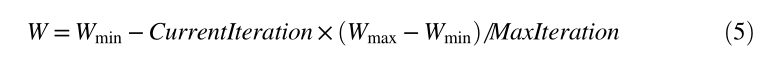
在这里，我们将 Wmin 和 Wmax 初始化为合适的最小和最大惯性权重。

现在，使用以下等式更新粒子的速度：

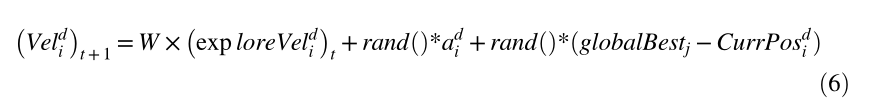
其中 rand 是范围 [0,1] 之间的任意数字，而 globalBest 是迄今为止获得的最佳解决方案。 exploreVel 是通过使用稍后部分中讨论的模糊推理机制来计算的。

​ 考虑一个如图 1 所示的神经网络，其中七个输入节点作为用户定位数据集的属性，三个输出节点作为类标签。 FPSOGSA 通过使用粒子在搜索空间中的探索和利用能力来训练神经网络。由于 PSO 在最后几次迭代中会出现饱和或收敛缓慢，因此粒子有时不会脱离其受限的搜索空间。这意味着均方误差 (MSE) 不会进一步降低，因此神经网络的准确性几乎没有变化。因此，为了让粒子能够探索新的搜索空间，我们提供了一个额外的速度分量 exploreVelij，它是从模糊推理系统 (FIS) 中推断出来的。这通过探索搜索空间中的新维度来增强粒子的搜索能力，从而增加获得更好的全局最佳解决方案的机会。如前所述，在这里我们在从 FIS 获得探索速度之前更新粒子的质量和加速度。这是因为 GSA 分量增加了质量相互作用，这在实现全局最优方面起着至关重要的作用，而且加速度分量用于更新第 (t + 1) 次迭代中的粒子速度。 FIS 将归一化当前最佳适应值 (NCBFV) 和粒子速度 (Velij) 作为输入，并使用下面讨论的模糊规则推断比例因子 ðSf Þ 和速度阈值控制参数 (Vtc) 作为输出本节。获得比例因子 Sf 是为了防止粒子超出其域，同时在搜索空间中获得额外的探索能力。

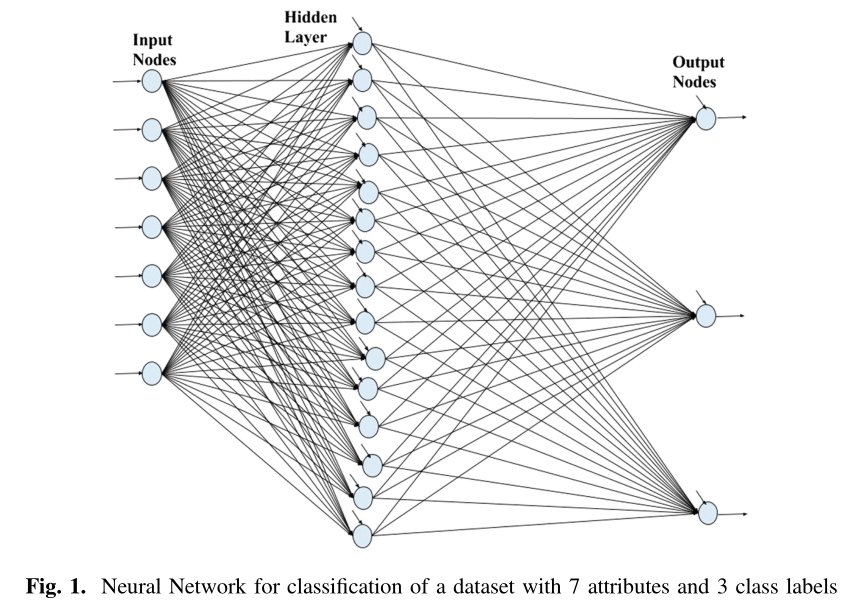
fig1 用于对具有 7 个属性和 3 个类标签的数据集进行分类的神经网络

NCBFV 计算如下：

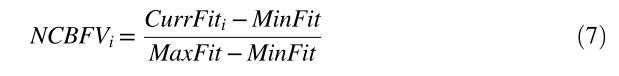
其中 CurrFiti 是粒子的当前适应度值，MinFit 是粒子在当前迭代之前获得的最小适应度值，MaxFit 是获得的最大适应度值。

阈值 (θ) 从速度阈值控制参数计算如下：

Velij 是在上一次迭代之前达到的粒子的最新速度。对于第一次迭代，exploreVelocityij 被认为与 Velij 相同。对于第一次之后的迭代，explorVelocityij 通过检查 θ 获得，如下所示：

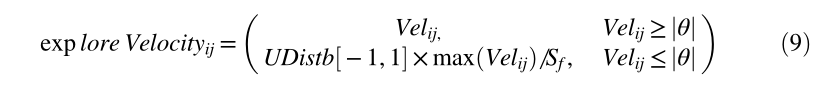
其中 UDistb[−1,1] 是 [−1,1] 范围内的均匀分布，max(\(Vel_ij\).) 是迄今为止获得的速度的最大值，θ 是从方程获得的阈值。 (8) 和 Sf 是作为 FIS 结果之一获得的比例因子。给定的模糊推理规则用于获得速度阈值控制参数 (Vtc) 和比例因子 (Sf) 的值，它们根据阈值 θ 确定粒子的 exploreVelocityij。

假设每条规则的权重为 1。根据变量的输入参数，适当地选择模糊范围，用于低/中/高/小和大。合适的三角或高斯隶属函数用于模糊化。

最后，使用以下方法将粒子的位置更新到下一个最佳位置：

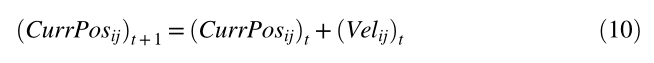
3.1 算法

1. 开始 FPSOGSA

2. 初始化——设置合适的迭代次数作为 MaxIteration 来训练 FNN。

   1. 初始化数据集并标准化 [-1, 1] 范围内的值。
   2. 根据数据集为 FNN 选择合适数量的输入、输出和隐藏节点。

3. 获得权重以训练神经网络 (NN)。

4. 随机初始化权重和偏差值。

5. 选择粒子数 (N) 并生成粒子的初始种群配置。

6. 计算每个粒子的适应度值并存储最佳和最差适应度值。计算——更新和计算搜索空间中粒子的参数。

7. 使用方程式更新 G。 (2) 并计算每个粒子的 globalBest。

8. 使用方程式计算每个粒子的质量、力和加速度。 （3），（1）和（4）分别。

9. 使用方程式更新惯性权重。 (5)。模糊化——获得 exploreVel g。使用方程获得并归一化粒子的当前最佳适应度值。 (7)。

10. 初始化模糊推理系统并使用上面定义的规则推断输出变量 Sf 和 VT。

11. 使用等式获得速度阈值 θ。 (8) 并使用等式计算 exploreVel。 (9)。

12. 使用方程式更新粒子的速度和新位置。 （6）和（10）分别。

13. 训练——通过传递获得的权重来训练 NN。

14. 获得 FNN 的均方误差并计算 FNN 的分类精度。

15. 重复上述过程，直到CurrentIteration = MaxIteration。

16. 结束 FPSOGSA。

4 实验计算结果与讨论

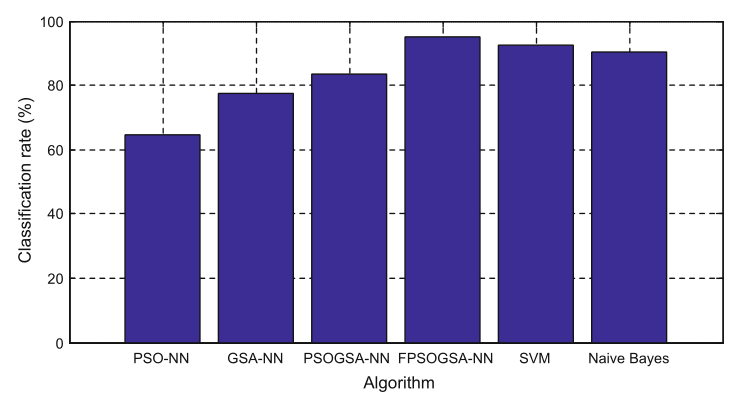
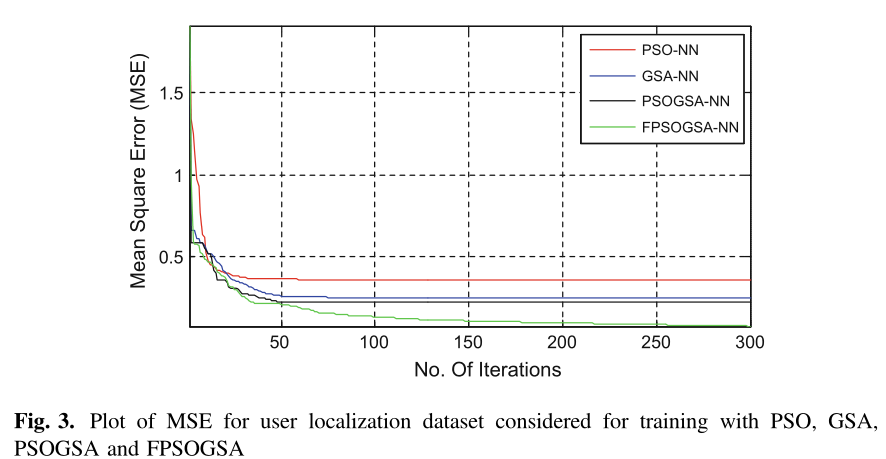
网络模型的输入是从各种路由器测量的无线信号强度的七个属性。获得的输出是根据用户的位置对用户进行分类的类标签。为神经网络结构选择了 15 个隐藏节点。神经网络的权重是从优化算法中获得的。图 1 所示的神经网络分别使用 PSO、GSA、PSOGSA 和提出的 FPSOGSA 算法进行训练，以获得训练神经网络所需的初始权重。这些权重经过 300 次迭代进一步优化，以获得数据集的最佳精度。用这些算法训练 300 次迭代后神经网络的分类精度如表 2 所示。所提出的 FPSOGSA 提高了神经网络的性能，因为它提高了探索新搜索空间的概率并利用了最佳粒子，因此他们克服了局部最小值。从图 3 所示的均方误差 (MSE) 值的急剧下降中可以明显看出这一点。该图还描述了此处考虑的各种其他优化策略在 300 次迭代中均方误差值下降的比较.

我们可以清楚地观察到，当通过 FPSOGSA 获得权重来训练神经网络时，误差非常小。因此，发现 FPSOGSA 的性能优于粒子群优化 (PSO)、引力搜索算法 (GSA) 和混合 PSOGSA（图 2）。

我们还比较了其他模型，例如 SVM 和朴素贝叶斯，它们是常用的模式分类方法。然而，我们选择使用神经网络是因为在 Sect 末尾解释的具体原因。 1. 这里，图 3. 显示了使用数据集的各种算法获得的分类精度

proudced
我们进行了十折交叉验证，并记录了十倍的平均值作为分类准确度。从获得的结果中，我们得出结论，带有神经网络的 FPSOGSA 给出了最高的分类率。

References

1. Bulusu, N., Heidemann, J., Estrin, D.: GPS-less low-cost outdoor localization for very small
   devices. IEEE Personal Commun. 7(5), 28–34 (2000)
2. Salazar, A.M., Warden, D.L., Schwab, K., Spector, J., Braverman, S., Walter, J.,
   Ellenbogen, R.G.: Cognitive rehabilitation for traumatic brain injury a randomized trial.
   JAMA 283(23), 3075–3081 (2000)
   PSO-NN GSA-NN PSOGSA-NN FPSOGSA-NN SVM Naive Bayes0
3. Nguyen, N.T., Bui, H.H., Venkatsh, S., West, G.: Recognizing and monitoring high-level
   behaviors in complex spatial environments. In: Proceedings of IEEE Computer Society
   Conference on Computer Vision and Pattern Recognition, vol. 2, II-620. IEEE (2003)
4. Pei, L., Liu, J., Guinness, R., Chen, Y., Kuusniemi, H., Chen, R.: Using LS-SVM based
   motion recognition for smartphone indoor wireless positioning. Sensors 12(5), 6155–6175
   (2012)
5. Cho, S.B.: Exploiting machine learning Techniques for location recognition and prediction
   with smartphone Logs. Neurocomputing (2015)
6. Zou, H., Lu, X., Jiang, H., Xie, L.: A fast and precise indoor localization algorithm based on
   an online sequential extreme learning machine. Sensors 15(1), 1804–1824 (2015)
7. Zadeh, L.A.: Fuzzy sets. Inform. control 8(3), 338–353 (1965)
8. Jang, J.S., Sun, C.T.: Neuro-fuzzy modeling and control. Proc. IEEE 83(3), 378–406 (1995)
9. Eberhart, R.C., Kennedy, J.: A new optimizer using particle swarm theory. In: Proceedings
   of the Sixth International Symposium on Micro Machine and Human Science, vol. 1, pp. 39–
   43 (1995)
10. Shi, Y., Eberhart, R.C.: Fuzzy adaptive particle swarm optimization. In: Proceedings of the
    2001 Congress on Evolutionary Computation, vol. 1, pp. 101–106. IEEE (2001)
11. Liu, H., Abraham, A., Zhang, W.: A fuzzy adaptive turbulent particle swarm optimisation.
    Int. J. Innovative Comput. Appl. 1(1), 39–47 (2007)
12. Mirjalili, S., Hashim, S.Z.M., Sardroudi, H.M.: Training feedforward neural networks using
    hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput.
    218(22), 11125–11137 (2012)
13. Nandy, S., Sarkar, P.P., Das, A.: Training a feed-forward neural network with artificial bee
    colony based backpropagation method. arXiv preprint arXiv:1209.2548 (2012)
14. Kawam, A.A., Mansour, N.: Metaheuristic optimization algorithms for training artificial
    neural networks. Int. J. Comput. Inf. Technolgy 1, 156–161 (2012)
15. Rashedi, E., Nezamabadi-Pour, H., Saryazdi, S.: GSA: a gravitational search algorithm.
    Inform. Sci. 179(13), 2232–2248 (2009)