各阶幻方的构造算法

UP | HOME

各阶幻方的构造算法

奇数阶幻方

拉-卢贝尔算法

这个算法又称“阶梯法”。算法如下：

1. 将1置于第一行中间。
2. 将下一个数字置于当前数字的右上角。如果已经处于方阵的边界，则放在方阵的对边（如图1中的2和4）。
3. 若出现下面两种情况，则将下一个数字放于当前数字的下方：
   • 当前位置的右上角已经有一个数字（如图2中的6和11）。
   • 当前位置已经是方阵的右上方（如图2中的16）。
4. 结束，如图3.

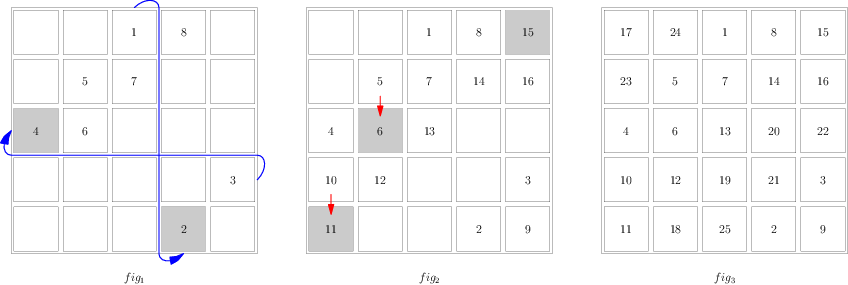
拉-卢贝尔算法

菱形算法

另一种由康韦（J.H.Conway）建立的算法被称为“菱形算法”，步骤如下（以5x5为例）：

1. 从左边中间开始，将奇数在方阵内填成一个菱形。
2. 将方阵分成5条对角线，每条对角线上有5个方格。如果图1所示。
3. 从第一条对角线开始将偶数填入剩余的空格内，图2中填满了前两条对角线。
4. 结束，如图3。

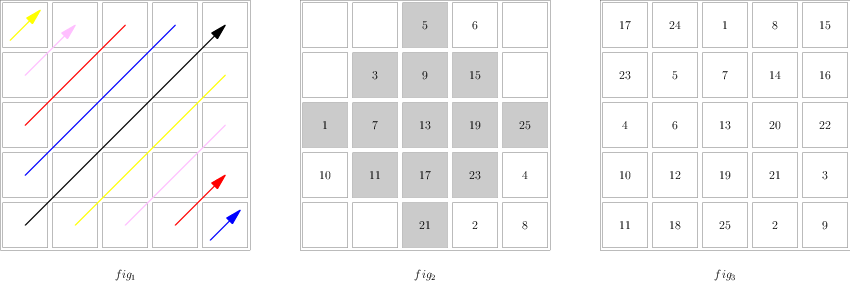
菱形算法

单偶数阶幻方

侓克斯算法

这个算法也是由康韦给出的。思想是将方阵分成多个2x2的小方阵，小方阵按照位置分成L、U、X三种类型。然后在大体上按照卢-拉贝尔算法来走，在每个小方阵中根据小方阵的类型来填数。具体算法如下：

1. 将方阵分成(2i+1)个(2x2)的小方阵，小方阵的分类这样确定：前i+1行是L类型，后面一行是U类型，最后的i-1行是X类型，然后交换第i+1行和第i+2行中间小方阵的类型。对于10x10的方阵如图1。
2. L、U、X的填法如图2。
3. 最终结果如图3。

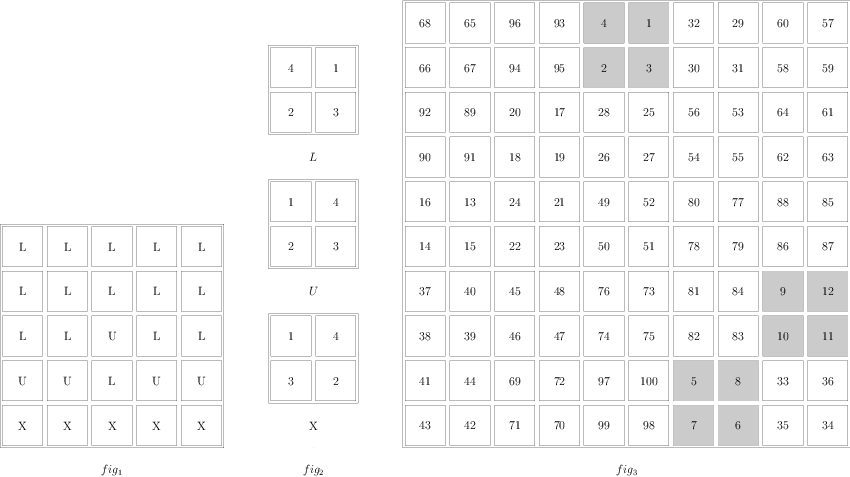
LUX算法

加法算法

将一个幻方加上另外一个幻方所得的和仍然具有幻方的特性，只是可能会有重复项，这是幻方的加法特性。下面的方法就是根据这个特性设计的，首先建立两个方阵A、B，具有幻方的特性（横、纵、斜和相同），然后让A加上B的i倍，就得到一个幻方。假如我们要作一个4i+2阶幻方（此处以14为例）。具体算法如下：

1. 先作一个14（4i+2）阶的方阵A，这个方阵分成4个7（2i+1）阶小方阵，每个小方阵是一个奇数阶的幻方，奇数阶幻方构造方法已经有了。如图1。
2. 再作一个14（4i+2）阶的方阵B，这个方阵只由0、1、2、3构成，具体作法如下：
   1. 第一列：3（i）个3,4（i+1）个0,5（i+2）个2,2（i-1）个1
   2. 前7（2i+1）列与都与第一列相同，只有第4（i+1）列例外，该列第一个3和第一个0交换位置。
   3. 后7（2i+1）列与前7（2i+1）列相同，不过3和0交换，1和2交换。
   4. 结果如图2。
3. 构造幻方C=A+i²B。如图3,C即所求。

加法算法

替代算法

这个是最难的一个。对于2i+2的幻方（以6为例）：

1. 将幻方分成A、B、C、D、E、F、G、H和I几个区,如图1。
2. 类似于双偶数阶幻方的分割算法，将处于上述分区中的格子填数，如图2。
3. 然后在空格上（i+1和3i+1行列）填上数，如图3。

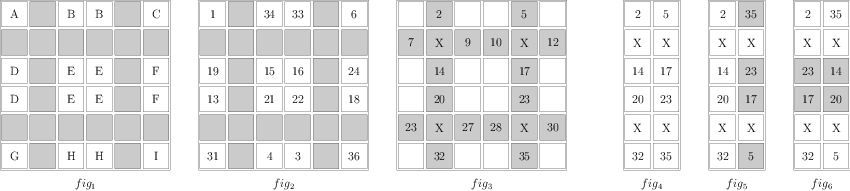
替代算法

好吧，太难了，中译本翻译得又很不清楚，不写了，等有机会看到更好的版本再加上。

双偶数阶幻方

分割算法

1. 将方阵分成16个小方阵，如图1。
2. 先在A、C、E、G、I方阵中填入数字，其他方阵跳过,如图2。
3. 再逆序（从右下往左上）赶往余下的数字,如图3。
4. 结束，如图3

分割算法

下面是一个8次的方阵：

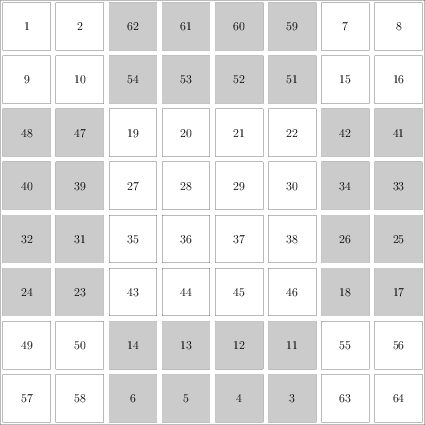
8次方阵

对角线算法

1. 将数字顺序填入方阵内,如图1。
2. 将方阵分成四个相同大小的方阵。并找出每个小方阵的对角线，如图1阴影部分。
3. 将阴影部分旋转180度，如图2。

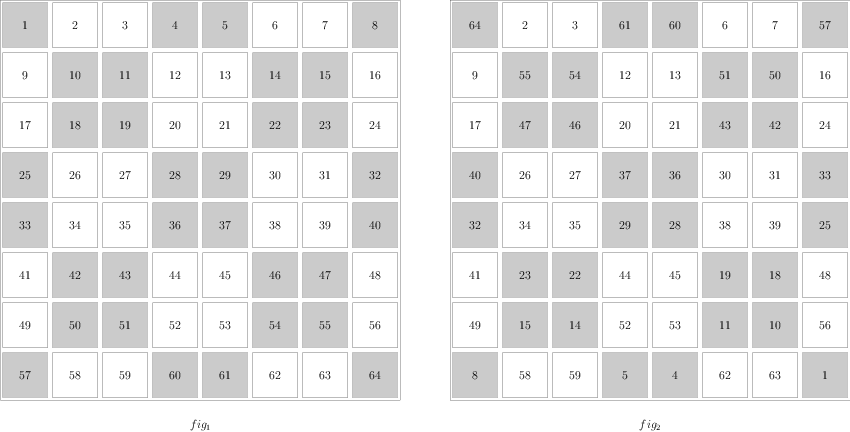
对角线算法

Date: 2012-12-06 四

Author: Hu Wenbiao

Org version 7.8.11 with Emacs version 24

Validate XHTML 1.0