20171022机器学习之线性回归-求时间与功率的关系(解决单项式线性方程)
应用问题:求下列数据中时间与功率的关系?
已知数据如下(数据之间以;号隔开):
数据:日期、时间、有功功率、无功功率、电压、电流、厨房电功率、洗衣机电功率、热水器的电功率
Date;Time;Global_active_power;Global_reactive_power;Voltage;Global_intensity;Sub_metering_1;Sub_metering_2;Sub_metering_3
16/12/2006;17:24:00;4.216;0.418;234.840;18.400;0.000;1.000;17.0
16/12/2006;17:25:00;5.360;0.436;233.630;23.000;0.000;1.000;16.0
16/12/2006;17:26:00;5.374;0.498;233.290;23.000;0.000;2.000;17.0
16/12/2006;17:27:00;5.388;0.502;233.740;23.000;0.000;1.000;17.0
16/12/2006;17:28:00;3.666;0.528;235.680;15.800;0.000;1.000;17.0
16/12/2006;17:29:00;3.520;0.522;235.020;15.000;0.000;2.000;17.0
16/12/2006;17:30:00;3.702;0.520;235.090;15.800;0.000;1.000;17.0
16/12/2006;17:31:00;3.700;0.520;235.220;15.800;0.000;1.000;17.0
。。。。。。
一、如何应用机器学习的线性回归算法,来预测出该数据中时间X 与 功率 Y之间的关系呢?
思路:1.首先该问题属于单项式方程的线性回归问题。
什么意思呢?很简单,把时间列看做X0->Xi,把功率看做Y0->Yi,那么剩下就是求解Y = aX + b的方程问题了;
b=偏差,按方程等式来推导的话,b=Y - aX,这里的Y就是我们的真实值功率,aX是我们的预测值,相减得出偏差值b
2.有了线性方程公式之后,我们需要求出最佳系数a,来使得通过X和Y训练数据之后的模型逼近真实值的线性曲线。
那么如何来求a呢?需要通过最大似然估算以二乘法!
下面具体来讲解下推导过程:
实际项目中我们的X可能会有很多,每一个特征值就是一个X,那么我们的方程很有可能变成
Y = a0X0 + a1X1 + a2X2 + ... + aiXi ,如下图1:

那么下面就是求这个Θ西塔的过程了,





python代码如下:
https://github.com/chenjunhaolefa/AI/blob/master/MachineLearning/LinearRegression01.py
实现后的预测图:
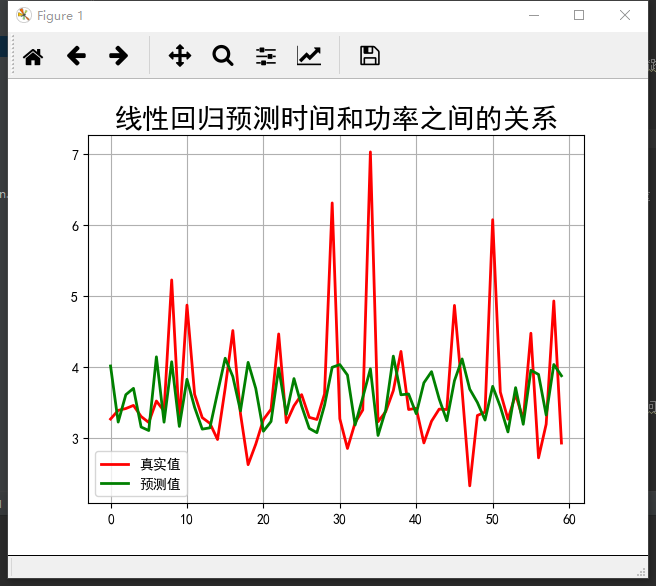
结论:时间和功率关系不大,那么我们再来看下功率和电流的关系吧。。。方法一样代码做了微调
代码:https://github.com/chenjunhaolefa/AI/blob/master/MachineLearning/LinearRegression02.py
功率和电流的预测图2:

结论:预测值和真实值基本拟合说明,功率和电流是强关系。大家明白了吗?






