《信号与系统》(二)
四、傅里叶变换与频率分析
周期信号的傅里叶级数
1.信号的正交分解
完备正交集:(1)三角函数级\({1, cos(n\Omega t),sin(n\Omega t),n=1,2,...}\),
(2)虚指数函数集\({e^{jn\Omega t},n=0,\pm1,\pm2,...}\)
任意信号f(t)可以表示为无穷多个正交函数之和:
上式称为信号的正交展开式,也称为广义傅里叶级数。
2.帕斯瓦尔定理
帕斯瓦尔方程:\(\int_{t_{1}}^{t_{2}} f^{2}(t) \mathrm{d} t=\sum_{i=1}^{\infty} \int_{t_{1}}^{t_{2}}\left[C_{i} \varphi_{i}(t)\right]^{2} \mathrm{~d} t\)
信号的能量 = 各正交分量的能量,即能量守恒定理
3.三角形式的傅里叶级数
设周期信号\(f(t)\),其周期为T,角频率\(\Omega = 2 \pi/T\),当满足狄里赫利条件时,可展开为三角形式的傅里叶级数。
\(f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos (n \Omega t)+\sum_{n=1}^{\infty} b_{n} \sin (n \Omega t)\)
直流分量+n次余弦分量+n次正弦分量
狄里赫利条件:在一个周期内,①函数连续或只有有限个第一类间断点,②函数极大值和极小值的数目应为有限个,③函数绝对可积
余弦形式的傅里叶级数:\(f(t)=\frac{A_{0}}{2}+\sum_{n=1}^{\infty} A_{n} \cos \left(n \Omega t+\varphi_{n}\right)\)
\(\left\{\begin{array}{l}A_{n}=\sqrt{a_{n}^{2}+b_{n}^{2}} \\ \varphi_{n}=-\arctan \frac{b_{n}}{a_n}\end{array} \quad\left\{\begin{array}{l}a_{n}=A_{n} \cos \varphi_{n} \\ b_{n}=-A_{n} \sin \varphi_{n}\end{array}\right.\right.\)
直流分量+基波(一次谐波)+二次谐波+……n次谐波
吉布斯线性:用有限项傅里叶级数表示有间断点的信号时,在间断点附近不可避免的会出现振荡和超调量。当选取的项数很大时,该超调量趋于一个常数,大约等于总跳变值的9%,并从间断点开始以起伏振荡的形式逐渐衰减下去。
4.周期信号波形对称性和谐波特性
①\(f(t)\)为偶函数,\(b_n\)=0,展开为余弦级数
②\(f(t)\)为奇函数,\(a_n\)=0,展开为正弦级数
③\(f(t)\)为奇谐函数\(f(t)=-f(t\pm T/2)\),傅里叶级数只含奇次谐波\(a_0=a_2=...=b_2=b_4=0\)
④\(f(t)\)为偶谐函数\(f(t)=f(t\pm T/2)\),傅里叶级数只含偶次谐波\(a_1=a_3=...=b_1=b_3=0\)
周期信号的频谱
1.指数形式的傅里叶级数
\(f(t)=\sum_{n=-\infty}^{\infty} F_{n} \mathrm{e}^{j n \Omega t}\)
傅里叶系数:\(F_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) \mathrm{e}^{-j n \Omega t} \mathrm{~d} t\)
表明:任意周期信号\(f(t)\)可分解为许多不同频率的虚指数信号之和。\(F_n\)是频率为\(n\Omega\)的分类的系数。\(F_0 = A_0/2\)为直流分量。
与三角形式的傅里叶系数的关系:\(F_{n}=\left|F_{n}\right| e^{j \varphi_{n}}=\frac{1}{2} A_{n} e^{j \varphi_{n}}=\frac{1}{2}\left(a_{n}-j b_{n}\right)\)
2.周期信号的频谱
频谱:周期信号分解后,各分量的幅度和相位对于频率的变化,分为幅度谱和相位谱
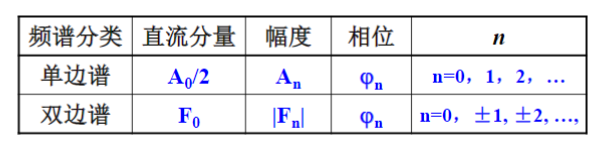
3.单边谱和双边谱的关系
\(\cos n \Omega t=\frac{1}{2}\left(e^{j \mu \Omega t}+e^{-j n \Omega t}\right)\)
\(F_{n}=\left|F_{n}\right| e^{j \varphi_{n}}=\frac{1}{2} A_{n} e^{j \varphi_{n}}\)
\(\left|F_{n}\right|=\frac{1}{2} A_{n} \quad \varphi_{n}=-\arctan \frac{b_{n}}{a_{n}}\)
\(|F_n|\)是n的偶函数,双边幅度谱的谱线高度为 单边幅度谱的一半,且关于纵轴对称;而直流分量值不变。\(\varphi_n\)是n的奇函数,双边相位谱可以由单边相位谱直接关于零点奇对称。
4.周期信号频谱的特点
①离散型,以基频\(\Omega\)为间隔的若干离散谱线组成
②谐波性:谱线仅含有基频\(\Omega\)的整数倍分量
③收敛性:整体趋势减小
周期矩形脉冲:
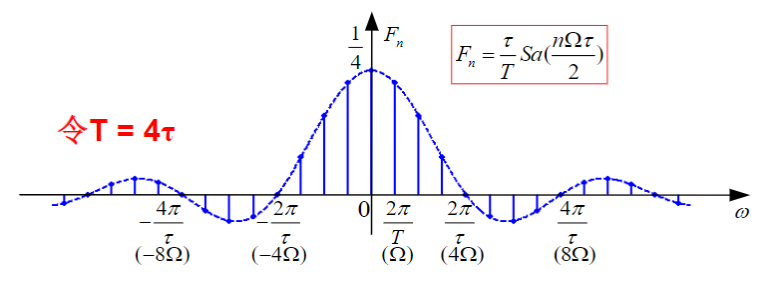
周期信号频谱的特点
1.周期信号的功率
周期信号一般是功率信号,平均功率为:
\(\begin{aligned} P &=\frac{1}{T} \int_{-\frac{\tau}{2}}^{\frac{7}{2}} f^{2}(t) d t=\frac{1}{T} \int_{-\frac{\pi}{2}}^{\frac{\tau}{2}}\left[\frac{A_{0}}{2}+\sum_{n=1}^{\infty} A_{n} \cos \left(n \Omega t+\varphi_{n}\right)\right]^{2} d t \\ &=\left(\frac{A_{0}}{2}\right)^{2}+\sum_{n=1}^{\infty} \frac{1}{2} A_{n}^{2}=\left|F_{0}\right|^{2}+2 \sum_{n=1}^{\infty}\left|F_{n}\right|^{2}=\sum_{n=-\infty}^{\infty}\left|F_{n}\right|^{2} \end{aligned}\)
这是帕斯瓦尔定理在傅里叶级数情况下的具体实现,周期信号平均功率=直流和谐波分量平均功率之和,对于周期信号,在时域中求得的信号功率与在频域中求得的信号功率相同。
频带宽度:在满足一定失真条件下,信号可以用某段频率范围的信号来表示,此频率范围称为频带宽度。①一般把第一个零点作为信号的频带宽度②对于一般周期信号,将幅度下降为\(\frac{1}{10}|F_n|_{max}\)的频率区间定义为频带宽度。③系统的通频带>信号的带宽,才能不失真。
2.非周期信号的频谱
当\(T \to \infty\)时,周期信号→非周期信号;
\(F_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) \mathrm{e}^{-j n \Omega t} \mathrm{~d} t\) → 0;
谱线间隔\(\Omega\) →0
离散频谱→连续频谱
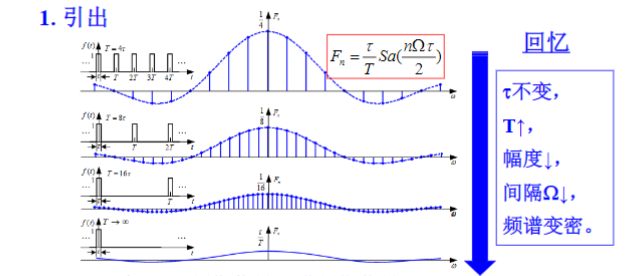
虽然各频率分量的幅度趋近于无穷小,但无穷小量之间仍有相对大小差别,故引入频谱密度函数。
频谱密度函数 \(T \to \infty\)时 \(\Omega \to d \omega ,\ \ n\Omega \to \omega\)
\(\begin{aligned} F(j \omega)=\lim _{T \rightarrow \infty} \frac{F_{n}}{1 / T} &=\lim _{T \rightarrow \infty} F_{n} T \text { (单位频谱上的频谱) }\\ &=\lim _{T \rightarrow \infty} \int_{-\frac{1}{2}}^{\frac{T}{2}} f(t) \mathrm{e}^{-j n \Omega t} \mathrm{~d} t \\ &=\int_{-\infty}^{\infty} f(t) \mathrm{e}^{-j \omega t} \mathrm{~d} t \end{aligned}\)
称为频谱密度函数,简称频谱密度或频谱
3.傅里叶变换
\(F(j \omega)=\int_{-\infty}^{\infty} f(t) e^{-j \omega t} d t\)
\(F(j\omega)\)称为\(f(t)\)的傅里叶变换,\(F(j\omega)\)一般是复函数,写为\(F(j\omega) = |F(j\omega)|e^{j\varphi(\omega)}\)
\(|F(j\omega)|\sim \omega\)幅度频谱,频率\(\omega\)的偶函数,\(\varphi(\omega)\sim \omega\)相位频谱,频率\(\omega\)的奇函数
傅里叶反变换:\(f(t)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} F(j \omega) e^{j \omega t} d \omega\)
\(\begin{aligned} &F(j \omega)=\mathscr{F}[f(t)] \\ &f(t)=\mathscr{F}^{-1}[F(j \omega)] \end{aligned}\) 或 \(f(t) \leftrightarrow F(j \omega)\)
傅里叶变换的充要条件:(所有能量信号都满足此条件)
\(\int_{-\infty}^{\infty}|f(t)| \mathrm{d} t<\infty\)
傅里叶变换及性质
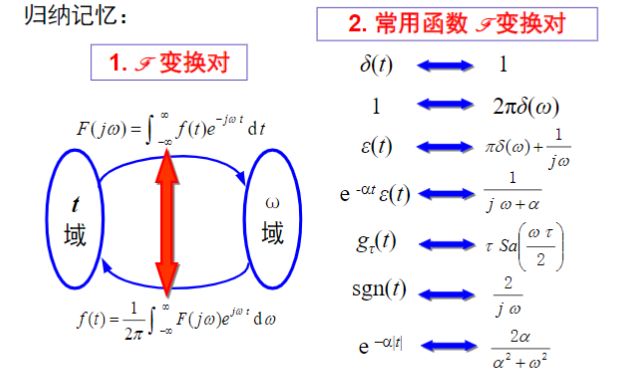
1.常用函数的傅里叶变换
2.线性
若 \(f_{1}(t) \leftrightarrow F_{1}(j \omega), \quad f_{2}(t) \leftrightarrow F_{2}(j \omega)\)
则\(a f_{1}(t)+b f_{2}(t) \leftrightarrow a F_{1}(j \omega)+b F_{2}(j \omega)\)
3.奇偶性
若 \(f(t) \leftrightarrow F(j \omega)\) 则 \(f(-t) \leftrightarrow F(-j \omega)\)
4.对称性
若 \(f(t) \leftrightarrow F(j \omega)\) 则 \(F(j t) \leftrightarrow 2 \pi f(-\omega)\)
5.尺度变换特性
若 \(f(t) \leftrightarrow F(j \omega)\) 则 \(f(a t) \leftrightarrow \frac{1}{|a|} F\left(j \frac{\omega}{a}\right)\),a为非零实数
信号的持续时间与信号占有频带成反比
6.时移特性
若 \(f(t) \leftrightarrow F(j \omega)\) 则 \(f\left(t \pm t_{0}\right) \leftrightarrow e^{\pm j \omega_{0}} F(j \omega), t_{0}\) 为实常数。
若 \(F(j \omega)=|F(j \omega)| e^{j \varphi(\omega)}\) 则 \(f\left(t \pm t_{0}\right) \leftrightarrow|F(j \omega)| \cdot e^{j\left[\varphi(\omega) \pm \omega t_{0}\right]}\)
7.频移特性
若 \(f(t) \leftrightarrow F(j \omega)\) 则 \(e^{\mp j \omega_0 t} f(t) \leftrightarrow F\left[j\left(\omega \pm \omega_{0}\right)\right]\),\(w_0\)为实常数,注意\(\pm\)号
实质是频谱搬移
8.卷积定理
时域卷积定理:若 \(f_{1}(t) \leftrightarrow F_{1}(j \omega), \quad f_{2}(t) \leftrightarrow F_{2}(j \omega)\) 则 \(f_{1}(t) * f_{2}(t) \leftarrow F_{1}(j \omega) F_{2}(j \omega)\)
频域卷积定理:若 \(f_{1}(t) \leftrightarrow F_{1}(j \omega), \quad f_{2}(t) \leftrightarrow F_{2}(j \omega)\) 则 \(f_{1}(t) f_{2}(t) \leftarrow \rightarrow \frac{1}{2 \pi} F_{1}(j \omega)^{*} F_{2}(j \omega)\)
9.时域微积分特性
若\(f(t)\leftrightarrow F(j \omega)\)
时域微分:\(f^{(n)}(t) \leftarrow \rightarrow(j \omega)^{n} F(j \omega)\)
时域积分:\(\int_{-\infty}^{t} f(x) \mathrm{d} x \leftarrow \rightarrow F(0) \delta(\omega)+\frac{F(j \omega)}{j \omega}\) 其中\(F(0)=\left.F(j \omega)\right|_{\omega=0}=\int_{-\infty}^{\infty} f(t) \mathrm{d} t\)
10.频域微积分特性
若\(f(t)\leftrightarrow F(j \omega)\)
频域微分:\((-jt)^nf(t) \leftarrow \rightarrow F^{(n)}(j \omega)\)
频域积分:\(\pi f(0) \delta(t)+\frac{f(t)}{-j t} \leftarrow \rightarrow \int_{-\infty}^{\omega} F(j x) \mathrm{d} x\) 其中\(f(0)=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(j\omega) \mathrm{d} \omega\)
11.相关定理
若 \(f_{1}(t) \leftrightarrow F_{1}(j \omega), \quad f_{2}(t) \leftrightarrow F_{2}(j \omega)\)
则 F \(\left[R_{12}(\tau)\right] \leftrightarrow F_{1}(j \omega) F_{2}^{*}(j \omega), \mathrm{F}\left[R_{21}(\tau)\right] \leftrightarrow F_{1}^{*}(j \omega) F_{2}(j \omega)\)
周期信号的傅里叶变换
1.能量谱
能量信号,能量有限信号:\(E =\lim_{T\to \infty} \int^T_{-T}|f(t)|^2 dt\)
能量方程:\(E=\lim _{T \rightarrow \infty} \int_{-T}^{T}|f(t)|^{2} \mathrm{~d} t=\int_{-\infty}^{\infty}|f(t)|^{2} \mathrm{~d} t=\frac{1}{2 \pi} \int_{-\infty}^{\infty}|F(j \omega)|^{2} \mathrm{~d} \omega\)
能量密度谱\(E(\omega)\):单位频率的信号能量,简称为能量频谱或能量谱
能量有限信号的能量谱\(E(\omega)\)与自相关函数\(R(\tau)\)是一对傅里叶变换
\(R(\tau)=\int_{-\infty}^{\infty} f(t) f(t-\tau) \mathrm{d} t\) \(E(\omega) = |F(j\omega)|^2\)
2.功率谱
功率信号,信号功率有限:\(P \stackrel{d e f}{=} \lim _{T \rightarrow \infty} \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}}|f(t)|^{2} \mathrm{~d} t\)
若信号能量E有限,则P=0;若信号功率P有限,则\(E=\infty\)
功率密度谱:单位频率的信号功率:\(\mathrm{P}(\omega)=\lim _{T \rightarrow \infty} \frac{\left|F_{T}(j \omega)\right|^{2}}{T}\)
维纳辛钦关系:功率有限信号的功率谱\(P(\omega)\)与自相关函数\(R(\tau)\)是一对傅里叶变换
\(R(\tau)=\lim _{T \rightarrow \infty}\left[\frac{1}{T} \int_{-\frac{\pi}{2}}^{\frac{T}{2}} f(t) f(t-\tau) \mathrm{d} t\right]\) \(P(\omega)=\lim _{T \rightarrow \infty} \frac{\left|F_{T}(j \omega)\right|^{2}}{T}\)
3.白噪声功率谱密度的估计
白噪声是指功率谱密度在整个频域内均匀分布的随机噪声
\(P_N(\omega)=N\) 功率密度谱是常数。
4.周期信号的傅里叶变换
周期信号→傅里叶级数,离散谱
非周期信号→傅里叶变换,连续谱
周期信号\(f_T(t)\)的频谱由冲激序列组成
\(F_{n}=\frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) e^{-j n \Omega t} d t\)
LTI系统的频域分析
1.基本信号\(e^{jwt}\)作用于LTI系统的响应
本章的响应指零状态响应
\(y(t)=H(j \omega) \cdot \mathrm{e}^{j \omega t} = h(t)*e^{jwt}\)
2.一般信号\(f(t)\)作用于LTI系统的响应
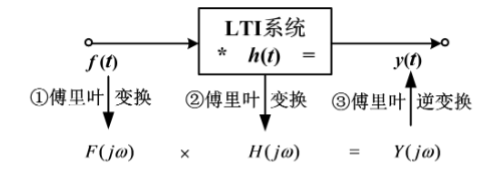
\(Y(j\omega)=F(j\omega)H(j\omega)\)
3.傅里叶变换分析法
4.傅里叶级数分析法
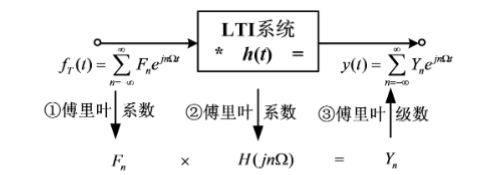
三角形式傅里叶级数表示:
5.频率响应函数
\(H(j\omega)\):系统零状态响应\(y(t)\)的傅里叶变换\(Y(j\omega)\)与激励\(f(t)\)的傅里叶变换\(F(j\omega)\)之比。即:\(H(j \omega)=\frac{Y(j \omega)}{F(j \omega)}\), \(H(j \omega)=|H(j \omega)| e^{j \theta(\omega)}=\frac{|Y(j \omega)|}{|F(j \omega)|} e^{j\left[\varphi_{y}(\omega)-\varphi_{f}(\omega)\right]}\)
\(|H(j\omega)|\)称为幅频特性,是\(\omega\)的偶函数
\(\theta(\omega)\)称为相频特性,是\(\omega\)的奇函数
求法:(1) \(\mathrm{H}(\mathrm{j} \omega)=\mathrm{F}[h(\mathrm{t})]\)
(2) \(\mathbf{H}(\mathbf{j} \omega)=\mathbf{Y}(\mathbf{j} \omega) / \mathbf{F}(\mathbf{j} \omega)\)
无失真传输和理想低通滤波器
1.无失真传输
系统对于信号的作用大体可分为两类,一类是信号的传输,一类是滤波。
信号无失真传输是指系统的输出信号与输入信号相比,只有幅度的大小和出现时间的先后不同,而没有波形上的变化。
\(f(t)\)经过无失真传输后,输出信号\(y(t)=K f\left(t-t_{d}\right)\),频谱\(Y(j \omega)=K e^{-j \omega t_{d}} F(j \omega)\)
无失真传输的条件:(1) 对 \(h(t)\) 的要求:
(2)对 \(\mathrm{H}(\mathrm{j} \omega)\) 的要求:
2.理想低通滤波器
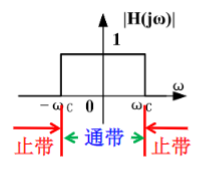
\(H(j \omega)=\left\{\begin{array}{cl}\mathrm{e}^{-j \omega t_{d}}, & |\omega|<\omega_{C} \\ 0, & |\omega|>\omega_{C}\end{array}=g_{2 \omega_{C}}(\omega) \mathrm{e}^{-j \omega t_{d}}\right.\)
\(|H(j \omega)|= \begin{cases}1, & |\omega|<\omega_{c} \\ 0, & |\omega|>\omega_{c}\end{cases}\)
\(\varphi(\omega)=-j \omega t_{d}\)
冲激响应:\(\begin{aligned} h(t) &=\mathrm{F}^{-1}\left[g_{2 \omega_{c}}(\omega) e^{-j \omega t_{d}}\right] \\ &=\frac{\omega_{c}}{\pi} \mathrm{Sa}\left[\omega_{c}\left(t-t_{d}\right)\right] \end{aligned}\)
是物理不可实现的,是非因果滤波器
3.物理可实现系统的条件
时域特性:因果条件 \(h(t)=0,t<0\)
频域特性:佩利-维纳准则(必要条件):
平方可积条件
并且 \(\int_{-\infty}^{\infty} \frac{|\ln | H(\mathrm{j} \omega) \|}{1+\omega^{2}} \mathrm{~d} \omega<\infty\)
取样定理
1.信号的取样
\(f_s(t) = f(t)s(t)\),取样间隔\(T_s\),取样频率\(f_s = 1/T_s\)
取样信号频谱\(F_s(j\omega)=\frac{1}{2\pi}F(j\omega)*S(j\omega)\)
矩形脉冲取样:
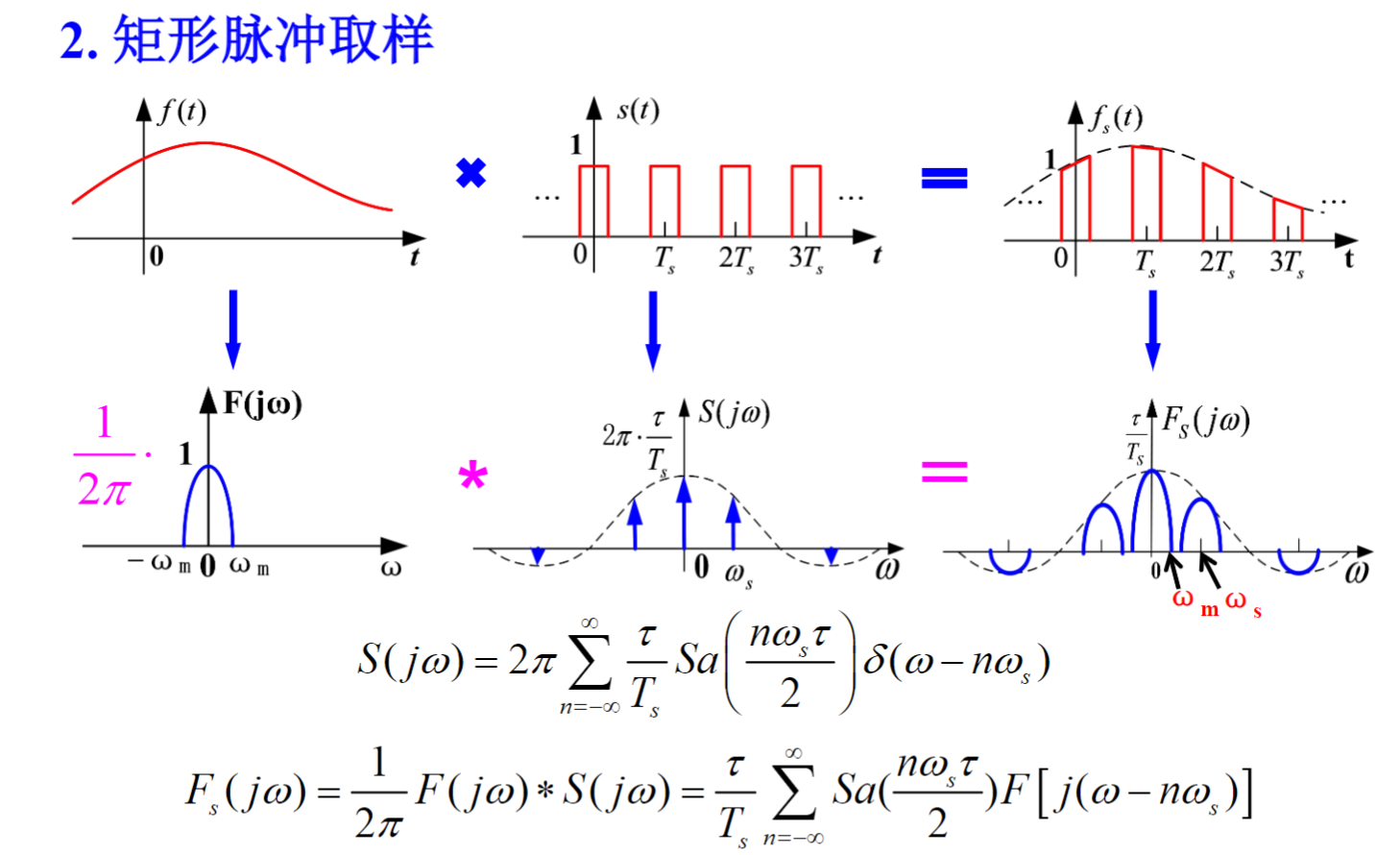
脉冲取样
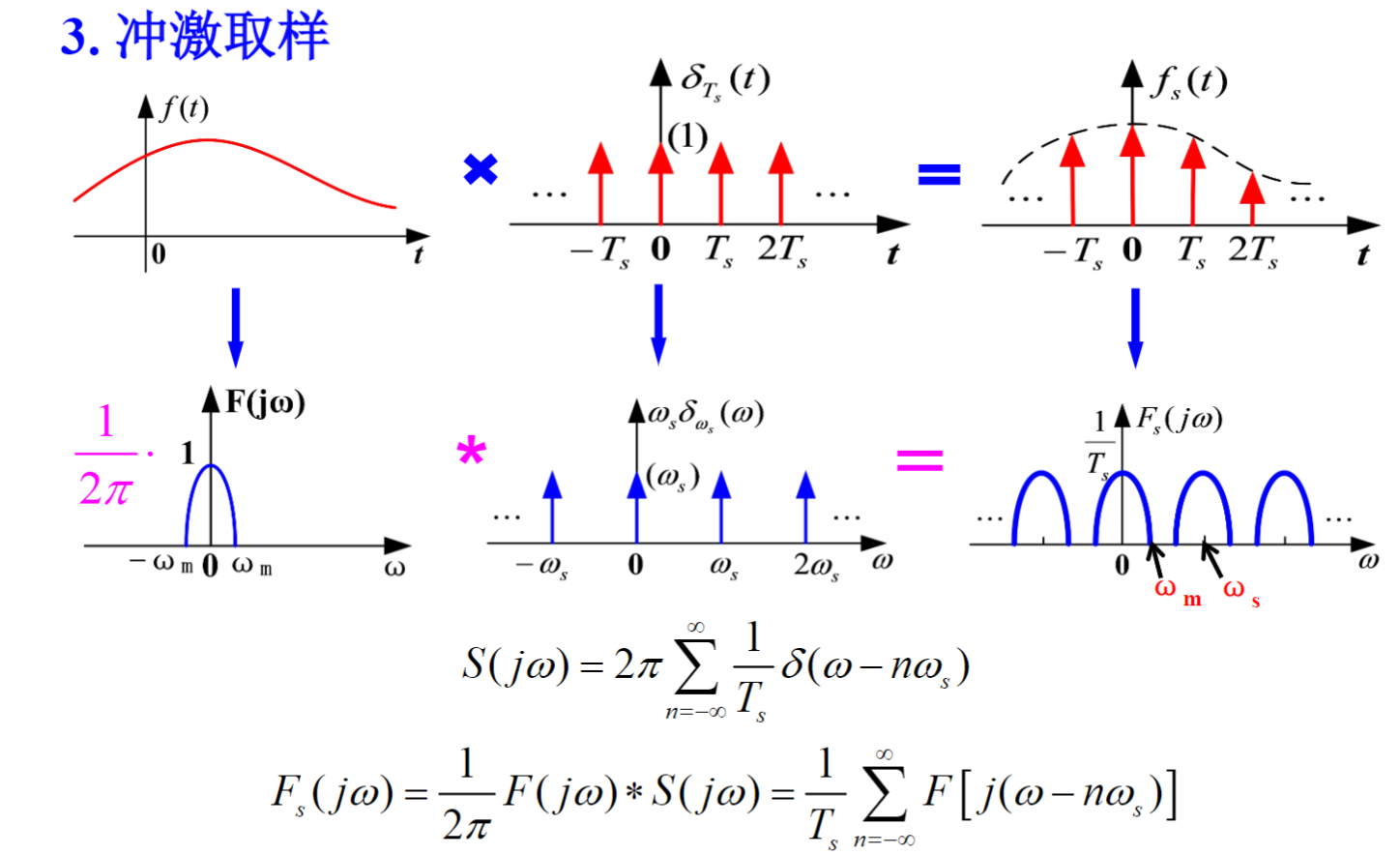
\(\omega_{\mathrm{s}} \geqslant 2 \omega_{\mathrm{m}}\),此时频谱不发生混叠,可以利用低通滤波器从\(F_s(j\omega)\)中提取\(F_(j\omega)\)。
2.取样定理(时域)
一个频谱在区间\((-\omega_m,\omega_m)\)以外为0的带宽信号\(f(t)\),可唯一地由其在均匀间隔\(T_s[T_s<1/(2f_m)]\)上的样值点\(f(nT_s)\)确定。
最低允许的取样频率(奈奎斯特频率)\(f_s=2f_m\)
3.取样定理(频域)
一个在时域区间\((-t_m,t_m)\)以外为0的时限信号\(f(t)\)的频谱函数\(F(j\omega)\),可唯一地由其在均匀频谱间隔\(f_s[f_s<1/(2f_m)]\)上的样点值\(F(jn\omega_s)\)确定。
\(F(j \omega)=\sum_{n=-\infty}^{\infty} F\left(j \frac{n \pi}{t_{m}}\right) \operatorname{Sa}\left(\omega t_{m}-n \pi\right), \quad t_{m}=\frac{1}{2 f_{s}}\)
离散傅里叶变换
1.傅里叶变换中连续到离散的演化
DTFT离散时间傅里叶变换:\(X(j \omega)=\sum_{n=-\infty}^{\infty} x[n] e^{-j \omega n}\)
缺点:时域序列的长度仍然是无限长,信号在频域仍然是连续的。
DFT离散傅里叶变换:\(X[k]=\sum_{n=0}^{N-1} x[n] e^{-j \frac{2 \pi}{N} n k}\)
DFS离散傅里叶级数:\(\tilde{X}(j k \Omega)=\frac{1}{N} \sum_{n=0}^{N-1} \tilde{x}(n) e^{-j k \Omega n}\)
2.五种傅里叶变换的比较
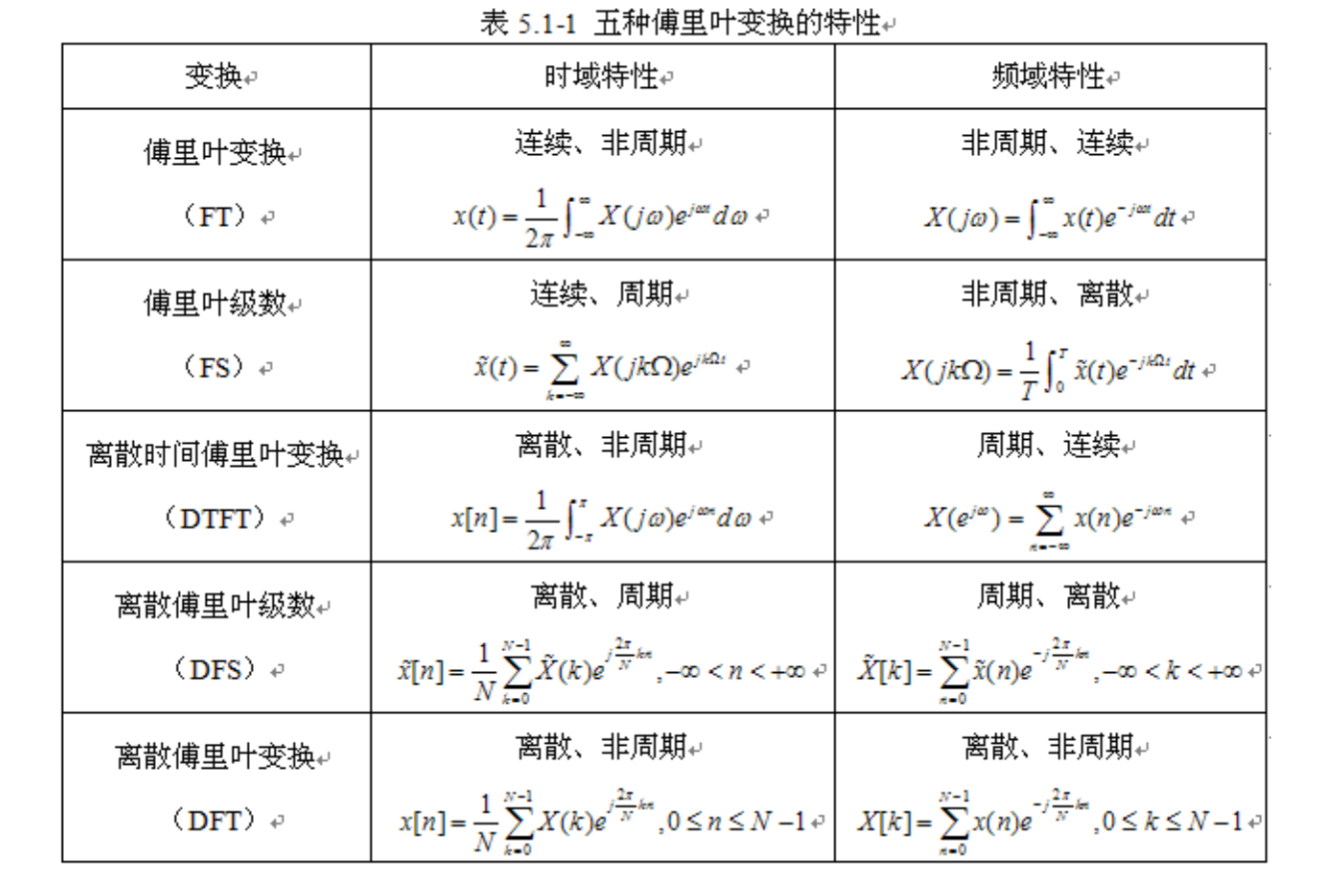
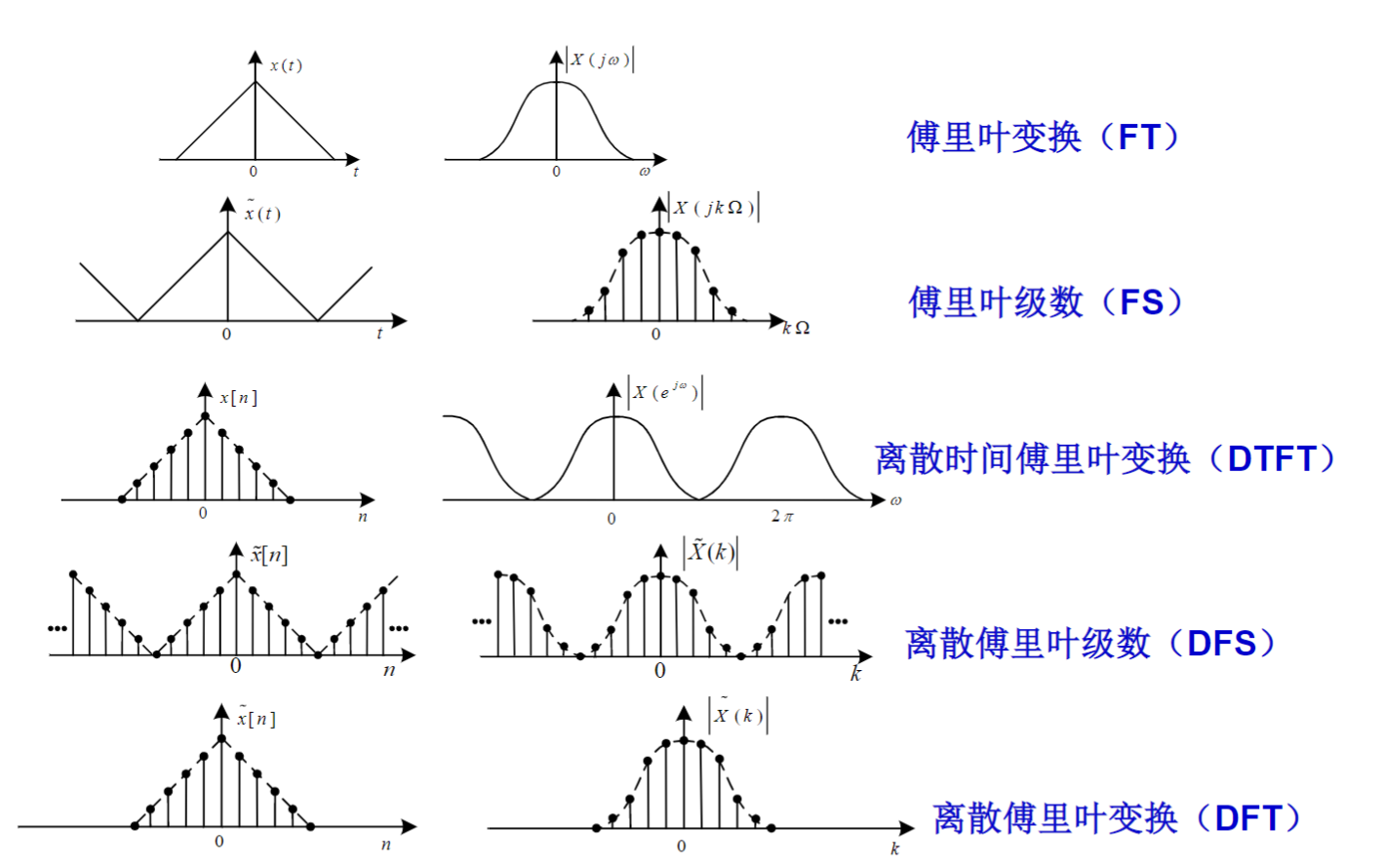
3.离散傅里叶变换定义(DFT)
定义:对于一个长度为N的离散信号\(x[n],n=0,...,N-1\),其离散傅里叶变换(DFT)为:\(X[k]=\sum_{n=0}^{N-1} x[n] W_{N}^{n k}, \quad k=0, ..., N-1\)
其中:\(W_{N}=e^{-j \frac{2 \pi}{N}}\)
离散傅里叶反变换:若\(X[k],k=0,...,N-1\)为长度为N的离散傅里叶变换系数序列,则称:\(x[n]=\frac{1}{N} \sum_{k=0}^{N-1} X[k] W_{N}^{-n k}, \quad n=0, ..., N-1\)
为\(X{k}\)的离散傅里叶反变换
物理意义:离散傅里叶变换是将一个有限信号\(x[n]\)表示成了N个离散正弦分量的加和,每个正弦分量的振幅和初始相位由系数\(X[k]\)给出。

