五一数学
Day 1
一、矩阵
就是 \(n\) 行 \(m\) 列的二维数组,用中括号框起来。
例如当 \(n = 2,m = 3\) 时,有一个矩阵 \(A\) 如下:
矩阵加减
将对应位置的两个元素相加,比较容易理解。
减法同理。
矩阵乘数
也是比较简单,用所有元素乘上这个数。
矩阵乘矩阵
定义 \(A\) 是 \(n\) 行 \(m\) 列,\(B\) 是 \(m\) 行 \(k\) 列。
设答案矩阵为 \(C\),那么 \(C\) 一定是 \(n\) 行 \(k\) 列。
具体来看做法:
可以有技巧的算:\(C_{i,j} = \text{A 中的第 i 行(横向)的每一个数去依次乘上 B 中的每一行的第 j 个数(纵向)的和}\),说起来比较绕,但是懂得了规律以后会发现十分简单。
这里给出一张图片比较好理解:
咕咕
代码
矩阵乘法:
点击查看代码
struct Matrix
{
int n,m;//n:矩阵行数 m:矩阵列数。
int a[105][105];//矩阵
Matrix ()//构造函数,作用:初始化矩阵为 0。
{
n = m = 0;
memset(a,0,sizeof (a));
}
};
Matrix operator * (const Matrix &a,const Matrix &b)
{
//重载 * 运算,起作用当且仅当是 Matrix 类型。
//&:取地址符,操作的时候是直接修改两个矩阵。
//const:防止运算的时候把运算的矩阵本尊破坏。
//注意类型。
Matrix ans;//返回的答案
int x = a.n,y = b.m;
int i,j,k;
for(i=1;i<=x;i++)
for(j=1;j<=y;j++)
//枚举每一个位置。
for(k=1;k<=a.m;k++)
//核心部分
ans.a[i][j] += a.a[i][k] * b.a[k][j];
return ans;
}
Day 2
一、模运算
逆元的定义
我们都知道模运算有分配率,但是只适用于乘法,除法不能运用分配率,要想求出除法的模运算,需要做出一些转化。
我们想要求出 \((a \div b) \bmod p\),但是硬算是求不出来的,需要做一些转化。
我们需要一个整数 \(x\),使得 \(a\times x \equiv a\div b\pmod{p}\)。
Tips:\(x\equiv y\pmod{p}\) 等同于 \(x \bmod p = y \bmod p\)
我们就称 \(x\) 为 \(b\) 的逆元。
求逆元的方法
费马小定理
如果 \(p\) 为质数且 \(1\le a < p,\gcd(a,p) = 1\),那么有 \(a^{p-1}\equiv 1\pmod{p}\)。两边同时除以 \(a\),得 \(a^{p-2}\equiv \frac{1}{a} (\bmod{p})\)。
所以 \(a\bmod p\) 的逆元是 \(a^{p-2}\),可以用快速幂计算。
欧拉定理
条件:\(\gcd(a,p) = 1\),如果 \(\gcd(a,p) \ne 1\),逆元不存在。
此时有 \(a^{\phi(p)}\equiv 1 \pmod{p}\)。
Tips: \(\phi(p)\) 表示从 \(1\) 到 \(n\) 中有多少个数与 \(p\) 互质。
那么 \(a\) 的逆元是 \(a^{\phi(p)-1}\)。
怎么计算?有两种算法。
1.暴力计算,复杂度 \(O(nlogn)\).
2.规律:\(\phi(n)=n(1-\frac{1}{p_1})(1-\frac{1}{p2})···(1-\frac{1}{p_t})\)。
点击查看代码
int get_phi(int n)
{
int phi = n;
int i;
for(i=2;i*i<=n;i++)
{
if(n%i==0)
{
phi = phi/i*(i-1);
while(n%i==0)//把质因子噶掉
n = n/i;
}
}
if(n!=1)
phi = phi/n*(n-1);
return phi;
}
我们设 \(k = p\div i,r = p \bmod i\)。
根据小学学过的 \(被除数 = 除数 \times 商 + 余数\),可以得出 \(p = k\times i + r\)。
转换成 \(k\times i + r \equiv 0\pmod{p}\)。
把 \(r\) 移到右边,得 \(k\times i \equiv -r \pmod{p}\)。
两边同时除以 \(i\),得出 \(-k \equiv \frac{r}{i} \pmod{p}\),也就是 \(-k \equiv \frac{1}{i} \times r\)。
继续移项,得出 \(\frac{1}{i}\equiv -\frac{k}{r} \pmod{p}\)。
C++ 语句为:inv[i] = 1ll*(p-k)%p*inv[r]%p。
其中 inv[i] 为 \(\frac{1}{i}\)。
代码:
点击查看代码
#include<bits/stdc++.h>
const int N = 1e6;
typedef long long ll;
using namespace std;
ll inv[N],n,p;//inv 数组表示 1/i。
int main()
{
cin>>n>>p;
inv[1] = 1;
int i;
for(i=2;i<=n;i++)
{
ll k = p/i,r = p%i;
inv[i] = 1ll*(p-k)%p*inv[r]%p;
}
for(i=1;i<=n;i++)
printf("%lld\n",inv[i]);
return 0;
}
exgcd
给定 \(a,b,c\),求任意一组整数解 \(x,y\),满足 \(ax+by=\gcd(a,b)\)。
我们令 \(d = \gcd(a,b)\),因为 \(\gcd(a,b)=\gcd(b,a\bmod b)\),所以把 \(b\) 和 \(a\bmod b\) 也写成类似的形式:
想要推出 \(x,y\),考虑把 \(a\bmod b\) 拆开,得出:
把括号拆开,得:
把带有 \(a\) 的凑到一起,带 \(b\) 的凑在一起,得:
此时,我们就发现这个式子与原来的式子一样了。所以:
此时递归求出 \(bx+(a\bmod b)\times y = d\) 的解即可。
终止条件?当 \(b=0\) 时,\(\gcd(a,b) = a\),所以让 \(x=1,y=0\) 即可。
可以用 \(\verb!struct!\) 维护三个元素 \(x,y,\gcd\),也可以顺便求出 \(\gcd(a,b)\) 了。
代码:
点击查看代码
struct pi
{
int x,y,d;
pii(int _x=0,int _y=0,int _d=0):x(_x),y(_y),d(_d){}
};
pi exgcd(int a,int b)
{
if(!b)
return {1,0,a};
pi GCD = exgcd(b,a%b);
return {GCD.y,GCD.x-a/b*GCD.y,GCD.d};
}
裴蜀定理
现在有一个问题:\(x,y,a,b\) 都是整数,那么 \(ax+by\) 的最小正整数,这说明了,只有答案是 \(\gcd(a,b)\) 的倍数时,方程才有解,这就是裴蜀定理。
现在要求 \(ax+by=c\),满足 \(c\) 是 \(\gcd(a,b)\) 的倍数,怎么做?
- 把得到的 \(x,y\) 同时乘 \(\dfrac{c}{\gcd(a,b)}\) 即可。
现在虽然求出了一组解,但是想要求出通解改怎么办?
- 设 \(x_0,y_0\) 是一开始 \(\verb!exgcd!\) 求出的一组解,那么通解可以写成 \(x=x_0+k\times \dfrac{b}{\gcd(a,b)},y=y_0-k\times \dfrac{a}{\gcd(a,b}\) 的形式,其中 \(k\) 是任意整数。
例题 1 - 同余方程
既然这道题有解,那么 \(\gcd(a,b)=1\)。
-
做法一:可以发现 \(x\) 是 \(a\) 的逆元。因为 \(b\) 不一定是质数,所以用欧拉定理解即可。
-
做法二:改写一下他的形式。既然 \(ax\bmod b=1\),那么 \(ax\) 一定可以写成 \(by+1\) 的形式,把他移项,变成 \(ax-by=1\),那么直接 \(\verb!exgcd!\) 即可。
但是题目要求得是最小正整数解,考虑通项公式。容易发现 \(x\equiv x_0 \pmod{b}\)。
由于 \(\gcd(a,b) = 1\),所以 \(x\equiv x_0 \pmod{b}\),容易发现答案就是 \(x_0 \bmod b\),所以 (...%mod+mod)%mod 即可。
二、素数 & 质数
判断一个数是否是质数
如何判断一个数为质数?可以从 \(1\) 暴力枚举到 \(n\),判断 n%i==0 即可。注意最大因子不会超过 \(\sqrt n\),所以可以从 \(1\) 枚举到 \(\sqrt n\),复杂度 \(O(\sqrt n)\)。
代码:
点击查看代码
bool is_prime(int n)
{
if(n<=1)
return 0;
if(n==2)
return 1;
if(n%2==0)
return 0;
int i;
for(i=3;i*i<=n;i++)//不要用 sqrt(n),复杂度爆表。
{
if(n%i==0)
return 0;
}
return 1;
}
但如果 \(n\) 加强到 \(10^{18}\),上述方法就通过不了,此时需要优化。
运用 \(\verb!Miller_Rabin!\) 进行素性测试。
素数往往满足一下两条定理的至少一条。
如果 \(n\) 是质数,那么有 \(n-1 = d\times 2^{r}\),存在一个 \(a < n\),那么
-
\(a^{d}\bmod n = 1\)
-
如果 \(0\le i<r\),那么有 \(a^{d\times 2^{i}} \bmod n = n-1\)
但是有些合数往往也满足上述定理之一,我们就要随机取一些 \(a\),增加素数成功的概率。
Tips:上述定理中,素数可能会满足一条或者两条,但一定会满足一条,但是有些合数可能不会满足,也可能会满足一条或者两条,需要进一步排查。如果满足了两条,成为素数的概率不会大于满足一条的概率。
质数筛
- 埃氏筛
点击查看代码
const int N = 1e6;
int not_prime[N],prime[N];
int cnt;
void make_era()
{
int i,j;
for(i=2;i<=n;i++)
if(not_prime[i])
for(j=i*2;j<=n;j+=i)
not_prime[i]=1;
for(i=1;i<=n;i++)
if(!not_prime[i])
prime[++cnt]=i;
}
复杂度大约为 \(O(loglogN)\)。
- 欧拉筛
点击查看代码
const int N = 1e6;
int not_prime[N],prime[N];
int cnt;
void make_ola()
{
int i,j;
for(i=2;i<=n;i++)
{
if(!not_prime[i])
prime[++cnt] = i;
for(j=1;j<=cnt;j++)
{
int x = prime[j]*i;
if(x>n)
break;
not_prime[x]=1;
if(i%prime[j]==0)
break;
}
}
}
复杂度为 \(O(N)\)。
Day 3
一、BSGS 算法
有一个式子,\(a^x \equiv b \pmod{p}\),给定 \(a,b,p\),求 \(x\)。
暴力
我们可以知道循环节长度为 \(p-1\)。这是因为费马小定理中,\(p\) 是质数,时间复杂度为 \(O(p)\)。
点击查看代码
int baoli (int a, int b, int p)
{
ll v = 1;
int x;
for(x=0;x<p-1;x++)
{
if(v==b)
return x;
else
v = 1ll*v*a%p;
}
return -1;
}
正解
因为循环节为 \(p-1\),所以只需要枚举前 \(p-1\) 个数。
将这 \(n\) 个数分组,设每组 \(s\) 个数,我们可以得出许多组,像下面一样。
\(1.\left\{a^0,a^1,...,a^{s-1}\right\}\)
\(2.\left\{a^s,a^{s+1},...,a^{2s-1}\right\}\)
我们就可以从第一组查找满足条件的 \(b\),如果没有找到,就从第二组找……这还是一种暴力的思想。
我们将两组联系起来,发现第二组每一个数都是第一组的 \(a^s\) 倍,将第二组的每个数处以 \(a_s\),就得出了第一组。
如果第二组存在 \(b\),那么第一组一定存在 \(\dfrac{b}{a^s}\)。
如果第 \(i\) 组出现 \(b\),那么第一组一定存在 \(\dfrac{b}{a^{s(i-1)}}\)。
可以运用哈希或者二分查找。
代码:
点击查看代码
set<ll> se;
int BSGS(int a,int b,int p)
{
int s = sqrt(p);
ll v = 1;
int i,j;
for(i=0;i<s;i++)
{
se.insert(v);
v = 1ll*v*a%p;
}
for(i=0;i*s<=p;i++)//看看答案是否在第 i 行里面
{
//要看 b*a^(-is) 是否在第零行出现
ll c = 1ll*b*ksm(ksm(a,i*s,p),p-2,p);
if(se.count(c)!=0)
{
ll v = ksm(a,i*s,p);
for(j=i*s;;j++)
{
if(v==b)
return j;
v = 1ll*v*a%p;
}
}
}
return -1;
}
懒人最爱的 set!!
复杂度为 \(O(\sqrt p \log p)\)
二、排列组合
排列
三个人中选两个人站成一排,考虑顺序。
有 \(6\) 种情况:
\(1.\left\{1,2\right\}\)
\(2.\left\{1,3\right\}\)
\(3.\left\{2,1\right\}\)
\(4.\left\{2,3\right\}\)
\(5.\left\{3,1\right\}\)
\(6.\left\{3,2\right\}\)
公式:
组合
三个人中选两个人站成一排,不考虑顺序。
有 \(3\) 种情况:
\(1.\left\{1,2\right\}\)
\(2.\left\{1,3\right\}\)
\(3.\left\{2,3\right\}\)
公式:
组合数有以下性质:
- \(C(n,n)=C(n,0)=1\)
显然 \(n\) 个数中选 \(n\) 个数的方案为 \(1\)。 - \(C(n,m)=C(n,n-m)\)
选 \(m\) 个数也等于不选 \(n-m\) 个,当然推式子也可以算出。 - \(\sum_{i=0}^n C(n,i)=2^n\)
\(0\) 到 \(n\) 个物品中有两种选择:选或不选,所以为 \(2^n\)。 - \(C(n,m)=C(n-1,m-1)+C(n-1,m)\)
详细讲一下第四个式子。
考虑第一个数选或不选,即两种可能。
如果选择了,那么要从剩下的 \((n-1)\) 个中选 \((m-1)\) 个;
如果没有选择,那么要从剩下的 \((n-1)\) 个中选 \(m\) 个,加起来就是 \(n\) 个中选 \(m\) 个,即 \(C(n,m)\)。
这里给出递推式代码:
点击查看代码
int C[1001][1001];
ll p;
void make_C(int n,int m)//用递推式做
{
int i,j;
for(i=0;i<=n;i++)
{
C[i][0] = 1;
for(j=1;j<=i;j++)
C[i][j] = (C[i-1][j-1]+C[i-1][j])%p;
}
return;
}
转化成图像怎么解释呢?通过画图,得出是一个杨辉三角。

-
当 \(n\ge 1\) 时,有 \(C(n,0)-C(n,1)+C(n,2)-C(n,3)+···=0\)
-
把 \(C(n,m)\) 展开 \(k\) 次,得:
例题 1
有 \(1\) 到 \(n\) 的 \(n\) 个数,每个数可以选很多次,从中选出 \(m\) 个数,不计顺序,求方案数。
先考虑只能选一次的情况。将这些书排序,其实就是求不等式 \(1\le a_1 < a2< ... < a_m \le n\) 的解的数量。答案为 \(C(n,m)\)。
那么如何把 \(\le\) 干掉呢?令 \(b_i = a_i+i-1\),那么原式就变成了 \(1\le b_1 <b_2<...<b_m \le n+m-1\)。此时的解为 \(C(n-m+1,m)\),把 \(b_i\) 还原成 \(a_i\),所以本题的答案就是 \(C(n+m-1,m)\)。
例题 2
给出 \(n,m,p\),求 \(C(n,m) \bmod p\),其中 \(1 \le n,m,p \le 10^{18}\)。
用分类讨论思想解决。
-
一、如果 \(n,m \le 10^{18},p=1\),答案是 \(0\)。
-
二、如果 \(n,m \le 1000,p \le 10^9\),那么可以用递推式来算。
-
三、如果 \(n,m\le 10^6\),\(p\) 是质数,那么怎么做呢?
用逆元+阶乘解决。
给出代码:
点击查看代码
int fac[1000001];
int find_C(int n,int m,int p)
{
fac[0] = 1;
int i;
for(i=1;i<=1000000;i++)
fac[i] = 1ll*fac[i-1]*i%p;
return 1ll*fac[n]*ksm(fac[m],p-2,p)%p*ksm(fac[n-m],p-2,p)%p;
}
- 四、如果 \(n \le 10^9,m \le 10^3\),\(p \le 10^9\)。
\(m\) 挺小的,所以突破口就在 \(m\) 上。猜测一下复杂度约为 \(O(m^2)\)。
我们进行约分,得:
Tips:\(\prod_{i=1}^{n}\) 在 C++ 中表示为:for(i=1;i<=n;i++) sum *= i。
把乘法拆开,分子与分母的项数都为 \(m\) 左右。
因为答案是整数,所以把分子与分母约分,直到分母全部为 \(1\) 为止。把分子乘起来就是答案。约分要用到 \(\gcd\),所以复杂度为 \(O(m^2\log n)\)。
点击查看代码
int fenmu[10001],fenzi[10001];
int find_C(int n,int m,int p)
{
int i,j;
for(i=1;i<=m;i++)
fenmu[i] = i,fenzi[i] = n-i+1;
for(i=1;i<=m;i++)
{
for(j=1;j<=m;j++)
{
int g = gcd(fenzi[i],fenmu[j]);
fenzi[i] /= g;
fenmu[j] /= g;
}
}
int ans = 1;
for(i=1;i<=m;i++)
ans = 1ll*ans*fenzi[i]%p;
return ans;
}
- 五、如果 \(n,m \le 10^9\),\(p \le 100\) 且是质数。
用 \(\verb!Lucas!\) 定理做。
\(\verb!Lucas!\) 定理的定义:
解释成人话就是:将 \(n,m\) 转换成 \(p\) 进制数,\(C(n,m)\bmod p\) 等于 \(n,m\) 在 \(p\) 进制下的各位相乘。
设 \(n\) 拆成 \(p\) 进制位 \(n_1,n_2,···,n_k\),\(m\) 拆成 \(m_1,m_2,···,m_k\),那么 \(C(n,m)\bmod p = \prod_{i=1}^k C(n_i,m_i)\)。
其中 \(n_i\) 与 \(m_i\) 都是一位数字。
通过发现 \(p\) 比较小,所以 \(C(n \bmod p,m \bmod p)\) 可以直接 \(O(p^2)\) 推出来,剩下的继续递归。
终止条件:\(m = 0\) 时,返回 \(1\)。
举个例子:当 \(n=221,m=110\text{(三进制)},p=3\)
那么有
此时的做法为:暴力预处理出组合数,然后用短除法将 \(n,m\) 分解成 \(p\) 进制,然后诸位计算即可。
复杂度 \(O(p^2+\log_p n)\)。
代码;
点击查看代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
int c[101][101];
int x[10001];
int y[10001];
int Lucas(int n,int m,int p)
{
//n,m<=10^9
//p <=100 且是质数
int i;
while(n!=0)
{
x[0]++;
x[x[0]] = n%p;
n /= p;
}
while(m!=0)
{
y[0]++;
y[y[0]] = m%p;
m /= p;
}
//x[1] x[2]....x[x[0]] 是 n 的 p 进制从低到高的表示
//y[1] y[2]....y[y[0]] 是 m 的 p 进制从低到高的表示
int ans = 1;
for(i=1;i<=x[0];i++)
ans = 1ll*ans*c[x[i]][y[i]]%p;
return ans%p;
}
signed main()
{
int n,m,p;
scanf("%d%d%d",&n,&m,&p);
int i,j;
for(i=0;i<=p;i++)
{
c[i][0] = 1;
for(j=1;j<=i;j++)
c[i][j] = (c[i-1][j-1]+c[i-1][j])%p;
}
printf("%d\n",Lucas(n,m,p));
return 0;
}
如果要求 \(C(n,m)\bmod 30\),怎么办?
将 \(30\) 质因数分解,\(30 = 2\times 3\times 5\),分别计算 \(C(n,m)\bmod 2,3,5\) 的结果,分别设为 \(x_1,x_2,x_3\),那么有
直接 \(\verb!CRT!\) 即可。
例题 3
洛谷 P4369
给你两个数 \(n\) 和 \(k\),请给出 \(k\) 个不同的组合数,使得它们的和相加为 \(n\)。
所谓不同,即对于 \(C(n1,m2)\) 和 \(C(n2,m2)\) 的组合数,\(n1 \ne n2\) 且
\(m2 \ne m2\),那么就称这两个组合数是不同的。
诈骗题。
众所周知,一个正整数 \(n\) 可以拆成 \(n\) 个 \(1\) 相加,既然要求 \(k\) 个组合数,那我们就让前 \((k-1)\) 个组合数为 \(1\),最后一个为 \(n-k+1\),就可以让和为 \(n\) 了。
那么前 \((k-1)\) 个组合数是什么呢?我们知道 \(C(n,0)=1\),那就让这些组合数的 “\(n\)” 都为 \(i\),这样就可以通过了。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n,k;
cin>>n>>k;
int i;
for(i=1;i<k;i++)
printf("%d 0\n",i);
printf("%d 1\n",k);
return 0;
}
例题 4
给出 \(n1,m1,n2,m2\),比较 \(C(n1,m2)\) 和 \(C(n2,m2)\) 的大小。
首先来讲一下 \(\log\)。
如果 \(x^y=z\),那么 \(log_x z=y\)。
有 \(\log (a\times b) = \log a+\log b\),\(\log(a\div b)=\log a-\log b\)。
Tips:这里的 \(\log\) 都是同底的,同底不影响大小。
如果 \(\log a< \log b\),那么 \(a < b\)。
根据上述式子,可以算出 \(\log C(n,m)\)。
首先 \(C(n,m) = \dfrac{n!}{m!(n-m)!}\)
所以 \(\log C(n,m)=\log n!-\log m!-\log (n-m)!\)
然后就可以计算了。想要求出 \(\log\) 的阶乘,可以从 \(\log i=\log i-1+\log i\) 考虑,用递推算即可。
点击查看代码
int faclog[1000001];
double logger(int n,int m)
{
faclog[0] = 0;
int i;
for(i=1;i<=100000;i++)
faclog[i] = faclog[i-1]+log(i);
return faclog[n]-faclog[m]-faclog[n-m];//比较 log(C(n1,m1)) 和 log(C(n2,m2))
}
例题 5
给出 \(n,k\),让你找到 \(k\) 个不同的组合数,使得这 \(k\) 个组合数的和最大。要求这些组合数 \(C(a,b)\) 满足 \(0\le b\le a\le n\),求出这个最大的和。\(n\le 10^6,k \le 10^5\)。
先把杨辉三角搞出来:

我们发现在三角中,最后一行的中间往往比较大,我们就可以考虑从中间优先选择。
那么第二大的数呢?肯定实在最大的上下左右。我们可以比较一下那个数更大。
可以向四周扩充几个点,维护一个候选集,从里面挑一个最大的,并且重新更新,重复 \(k\) 次即可。
就是一个裸的 \(\verb!BFS!\)。
例题 6
咕咕
三、抽屉原理
定义:\((n+1)\) 个物品放入 \(n\) 个抽屉里,至少有一个抽屉有多余 \(1\) 个物品。
推广:把 \((kn+1)\) 个物品放在 \(n\) 个抽屉里,必然有一个抽屉有 \((k+1)\) 个物品。
例题 1
给定 \(n\) 个数,随便选择任意个数,使得它们的和是 \(c\) 的倍数,任意给出一组解。\(c \le n \le 10^5\)。
引入前缀和。
\(sum_i = a_1+a_2+···+a_i\)
如何求出 \(l\) 到 \(r\) 的和?是 \(a_l+···+a_r\),即 \(sum_r-sum_{l-1}\)。
有了前缀和后,该怎么解题呢?
发现前缀和是连续的一段和,那我们就让题目复杂一点,即必须选连续的一些数。
把每个前缀和对 \(c\) 取模,如果 \(sum_i \bmod c =0\),那么这一段就是答案,否则放到 \((c-1)\) 个抽屉里面,那么肯定有两个前缀和放在一个抽屉里面,那么多出来的和就一定是 \(c\) 的倍数。
例题 2
洛谷 P2218
平面上有 \(n\) 个点,每个点有坐标 \((x_i,y_i)\),用 \(3\) 个 \(k\times k\) 的正方形覆盖所有点(平行于坐标轴),求最小的 \(k\)。\(1 \le n \le 5\times 10^4\)。
我们先随便定一个 \(k\),例如 \(k = 100\)。
假设现在已经覆盖住了所有点,那么 \(k=150\) 的时候,可以覆盖住吗?或者 \(k=50\) 的时候,可以全部覆盖吗?
答案分别是可以、不可以。
我们可以先找到边缘的四个点,即左、右、上、下。然后画一个大正方形,根据抽屉原理,一定会有一个正方形盖住两个点,所以这两个点就会成为正方形的顶点。
于是我们可以暴力枚举盖住哪个角,暴力枚举三次,最后检验一下每个点是否都被覆盖即可。
四、容斥原理
定义:有 \(A_1\) 个学语文的人,\(A_2\) 个学语文的人。
那么 \(A_1 \cap A_2\) 表示同时学语文和数学的人, \(A_1 \cup A_2\) 表示学语文或学数学的人。
可以得出 \(|A_1 \cap A_2|= |A_1|+|A_2|-|A_1 \cap A_2|\)。
画个图好理解:咕咕。
此时又出现了学英语的人,\(A_3\)。
有
此时又双叒叕出现了打游戏的人,\(A_4\)。
可以根据上面的式子的出来,但是比较复杂,懒得列出来了()
骗你的我这么勤奋,当然会列出来呢。
快给我点赞点赞点赞!!
可以总结出 \(n\) 个种类的人时,容斥原理的公式。
例题 1 - \(N\) 对夫妻问题
奇怪的名字。
\(n\) 对夫妻,一共 \(2n\) 个人。把他们排成一圈,满足每对夫妻都不相邻且旋转后相同的方案算一种,求方案数。
先考虑随坐的方案数,为 \((2n-1)!\)。
我们先强制让一对夫妻相邻,即 \((2n-1)!-C(n,1)\)。
把那一对夫妻绑在一起,看成一个人,此时就剩下了 \((2n-1)\) 个人,方案数为 \((2n-2)!\times C(n,1)\)。
但是我们可以把一夫一妻调换位置,所以要 \(\times 2\)。
整理一下,让一对夫妻相邻的方案数为 \((2n-1)!-C(n,1)\times (2n-2)!\times 2\)。
此时算完了吗?并没有,因为有算重的情况。
例题 2
给出 \(n\),询问 \(1\) 到 \(n\) 中有多少个数可以表示成 \(x^y,y>1\) 的形式。\(1\le n \le 10^{18}\)。
Day 4
一、解 方 程
是的你没看错,这一章讲的就是解方程。
二元一次方程
先给出一组二元一次方程:
用 \(\mathfrak{1}\) 式减去 \(\mathfrak{2}\) 式,得 \(2x_2=4\),可以算出 \(x_2 = 2\),随便带入一个式子,得 \(x_1=3\)。
多元一次方程
以此类推,可以算出三元、四元等方程组中。
给出一个多元一次方程组:
怎么解呢?可以用高斯消元来解决。
高斯消元的基本逻辑:每一次消掉一个未知数,减少一个方程,最后得到一个一元一次方程来求解的方法。
先给一个例子:
把他们对齐,并补齐系数(没有字母则为 \(0\))。
成为:
可以抽象看成一个矩阵乘法:
把等式的右边提到左边,得:
接下来开始高斯消元:
先把第一行同时乘上一个数,此时第二行的每个元素都加上第一行的对应的数乘上这个倍数。
这个倍数该怎么选择呢?通常情况下,第二行第一列的这个数,需要加上第一行第一列的数乘上这个倍数,使得第二行第一列的数为 \(0\)。
我们来进行第一次高斯消元:
可以看到如果倍数选了 \(-5\),此时第二行第一列的数为 \(5+(-5)\times 1=0\),第二行第二列的数为 \(3+(-5)\times 1=-2\),第二行第三列的数为 \(0+(-5)\times 4=20\),第二行第四列的数为 \(25+(-5)\times 19=70\)。
留坑待补。
二、扩展矩阵
如果有两个 \(n\times n\) 的矩阵,他们两个相乘,为 \(C\) 矩阵,如果 \(C\) 矩阵的对角线为 \(1\),其他数为 \(0\),那么就称 \(C\) 矩阵为单位矩阵。
我们就把 \(A\) 和 \(B\) 互相称为逆矩阵。
\(B\) 是 \(A\) 的逆矩阵,\(A\) 也是 \(B\) 的逆矩阵。
\(A\) 和 \(B\) 有以下性质:
- \(AB=BA=I^n\)
留坑待补。
三、概率
引入一个例子:扔一个骰子,每一面朝上的概率为多少呢?
因为骰子有 \(6\) 个面,每个面上都有一个数字,所以这些概率相等,都为 \(\dfrac{1}{6}\)。
把 \(1,2,3,4,5,6\) 这几个数称为样本空间,其中任意一个数称为样本点。事件是这些样本点的集合,即样本点相加为事件。
先来熟悉一下集合:
两个集合,\(A=\left\{1,2,3\right\},B=\left\{2,3,4\right\}\)。
\(A\cap B =A\cdot B=\left\{2,3\right\}\),即 \(A\) 与 \(B\) 共有的部分。
\(A\cup B=A+B=\left\{1,2,3,4\right\}\),即 \(A\) 与 \(B\) 中出现过的数。
\(A-B=A-A\cdot B=\left\{1\right\}\),即在 \(A\) 中 \(B\) 没有出现过的数。
把 \(P(A)\) 称为事件 \(A\) 发生的概率。注意每个样本点的概率不一定相等,一个事件的概率就是事件内样本点的概率的和。
概率有一些性质:
-
\(0\le P(A) \le 1\)。
-
假设样本空间有 \(n\) 个样本点,\(B_1,B_2,...,B_n\),那么 \(\sum_{i=1}^n P(B_i) = 1\)。
-
如果 \(P(A)=1\),那么把 \(A\) 称为必然事件;若 \(P(A)=0\),称 \(A\) 为不可能事件。
把 \(P(A|B)\) 称为在 \(B\) 发生的情况下,发生 \(A\) 的概率,这就是条件概率。
举个例子:当 \(P(\text{扔到 1|扔出的点数在 1 到 3 之间})=\dfrac{1}{3}\)。
当 \(A=\left\{1,2,3\right\},B=\left\{1,2,5\right\},P(A|B)=\dfrac{2}{3}\)。就是 \(3\) 个中满足 \(2\) 个概率的条件。
条件概率有一个简单的公式:
给一张图片加以解释:
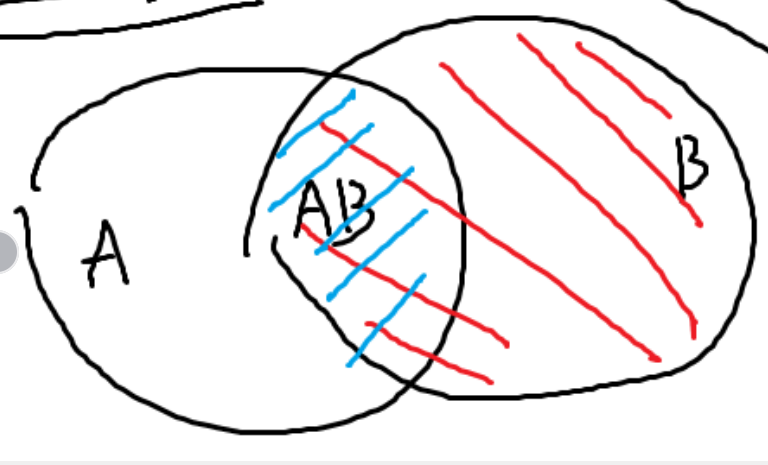
如果 \(B\) 发生了,就是红色的部分,如果 \(A\) 同时发生,就是蓝色部分。所以就可以得出了上述公式。
同时乘上 \(P(B)\),也可以得出 \(P(A|B)P(B)=P(AB)\)。
如果 \(A\) 事件发生,而 \(B\) 事件不发生,那么把这两个事件称为独立事件。
若 \(A\) 与 \(B\) 是独立事件,那么:
与条件概率相结合,可以得出:
那么
四、期望
继续扔骰子,扔到每个数的概率为 \(\dfrac{1}{6}\),求每个数的期望。
啥是期望?也就是每个事件的权值 \(\times\) 事件的概率并求和,那么扔骰子的概率为:
那么求扔出的数的平方的期望呢?
为:
期望也有一些性质:
- 期望的和 \(=\) 和的期望。例如有两个骰子:一个是正常的,每个数的概率都是 \(\dfrac{1}{6}\);第二个骰子被 \(\verb!TZF!\) 施了魔法,扔出 \(6\) 的概率是 \(\dfrac{95}{100}\),其他 \(5\) 个数字都是 \(\dfrac{1}{100}\),那么有:
换成平方也可以:
例题 1
有 \(3\) 张形状相同的卡片,一张两面都是黑色,一张两面都是红色,一张一面红一面黑。随机取出一张放在桌子上,朝上的为红色,那么另一面为黑色的概率是多少?
根据条件概率的计算,可得:
例题 2
\(n\) 个人按照一个顺序依次抓阄,每个人抓到了以后立即打开,当有人抓中后,游戏结束(只有一个“中”)。问游戏是否公平,并说明理由。
公平。理由如下:
第一个人抽到的概率为 \(\dfrac{1}{n}\)。
第二个人抽到的概率为 \(\dfrac{n-1}{n}\cdot \dfrac{1}{n-1}=\dfrac{1}{n}\)。
第三个人抽到的概率为 \(\dfrac{n-1}{n}\cdot \dfrac{n-2}{n-1}\cdot \dfrac{1}{n-2}=\dfrac{1}{n}\)。
以此类推,可以得出概率都是 \(\dfrac{1}{n}\),所以公平。
例题 3
设男女人口比例为 \(51:49\),男人色盲概率为 \(2\%\),女人色盲的概率为 \(0.25\%\),现随机抽到了一个人为色盲,请问该人为男人的概率是多少。
条件概率式子为:
懒得算了。
例题 4
一个人左右口袋里面各有一盒火柴,每盒 \(n\) 支。每次抽烟时随机选一盒拿出一只并用掉,由于习惯原因,选右面口袋的概率是 \(p>\dfrac{1}{2}\)。问:下述两种概率是否相等?并求出概率的值。
-
到某次他发现取出的这一盒已经空了,这时另一盒剩下 \(m\) 支。
-
他用完某一盒时,另一盒恰好有 \(m\) 支火柴。
我们可以列出左口袋与有口袋摸的概率:左边为 \(1-p\),右边为 \(p\)。
如果有 \(n\) 个火柴,发现取完了以后,此时取了 \((n+1)\) 次。
留坑待补。
例题 5
小葱和小泽面前有三瓶药,其中两瓶是毒药,一瓶是果汁,每个人必须喝一瓶。
小葱和小泽各自选择了一瓶药,小泽手速比较快,把药喝了下去,然后就挂掉了。
小葱想要活下去,他看到手上的药陷入了沉思——他应该喝掉手上的这一瓶还是换成剩下的一瓶呢?
两个人选择的药一共有 \(6\) 种情况,运用条件概率可以得出以下式子:
所以换或者不换,无所谓。
例题 6
上一个问题的扩展——“三门问题”。
三个门,一个里面有车,剩下的两个有 \(\verb!mie~mie~!\) 叫的羊,现在你选择了一个门,主持人知道哪个门有车、哪个门有羊。
留坑待补。
例题 7
小葱想要过河,过河有两条路:
-
一条路有 \(100\) 个石头,每个石头有 \(\dfrac{1}{100}\) 的概率会挂掉。
-
一条路有 \(1000\) 个石头,每个石头有 \(\dfrac{1}{1000}\) 的概率会挂掉。
小葱应该走哪条路呢?
这个问题相对比较简单。
第一条路存活的概率:\((\dfrac{99}{100})^{100}\)。
第二条路存活的概率:\((\dfrac{1}{1000})^{1000}\)
可以用计算器计算。
那么如果在数学考试中,不让用计算器呢?那该怎么做呢?
先把指数约分一部分,就成为了: \(\dfrac{99}{100}\) 和 \((\dfrac{999}{1000})^{10}\)。
我们都知道 \(\dfrac{999}{1000}>\dfrac{988}{999}>\dfrac{997}{998}>...>\dfrac{2}{3}>\dfrac{1}{2}\)。
所以 \((\dfrac{999}{1000})^{10}>\dfrac{999}{1000}\times ... \times \dfrac{990}{991}=\dfrac{99}{100}\)。
所以 \((\dfrac{999}{1000})^{1000}>(\dfrac{99}{100})^{100}\)。
所以答案是不过河走第二条路。
例题 8
小胡站在原点,手里拿着两枚硬币。抛第一枚硬币正面向上的概率为 \(q\),第二枚正面向上的概率为 \(r\)。
- 阶段一:小胡开始抛第一枚硬币,每次抛到反面小胡就向 \(y\) 轴正方向走一步,直到抛到正面。
- 阶段二:接下来小胡继续抛第一枚硬币,每次抛到反面小胡就向 \(z\) 轴正方向走一步,直到抛到正面。
- 阶段三:现在小胡想回来了,于是他开始抛第二枚硬币,如果小胡抛到正面小胡就向 \(y\) 轴的负方向走一步,否则小胡就向 \(z\) 轴的负方向走一步。
现在小胡想知道他在往回走的时候经过原点的概率是多少呢?
分析:留坑待补。
式子:
其他
鸣谢
由于本人对关于膜运算的掌握较差,于是大部分参考的是 SYZ 大佬的博客
同时在更好的讲解时,参照了 TZF 大佬的博客 与 ZHZ 大佬的博客。
同时感谢 QZH 大佬的博客给了这篇博客创作的动力(\(\verb!QZH!\) 大佬写了 \(1000\) 多行/bx/bx/bx)。
还有 CZH 大佬的支持 %%%%%%%%%%%%%%%。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号