图论刷题
图论刷题
一道简单题
一张 \(n\) 个点 \(m\) 条边的图，每次连续走两步（中间的点不算遍历到），可能遍历不完整个图，求至少加几条边才可以遍历玩（可以重复经过一些点）。
U468170
给定一张无向图，\(1\) 号点有一个箱子，初始在点 \(x\)，需要把箱子拉到 \(n\) 号点，或报告无解。（不能走到有箱子的点上，和箱子相邻时，可以拉箱子，也可以不拉）
P5304
J 国有 \(n\) 座城市，这些城市之间通过 \(m\) 条单向道路相连，已知每条道路的长度。
一次，居住在 J 国的 Rainbow 邀请 Vani 来作客。不过，作为一名资深的旅行者，Vani 只对 J 国的 \(k\) 座历史悠久、自然风景独特的城市感兴趣。
为了提升旅行的体验，Vani 想要知道他感兴趣的城市之间「两两最短路」的最小值（即在他感兴趣的城市中，最近的一对的最短距离）。
ARC173D
给定一张 \(N\) 个点 \(M\) 条边的有向图，每条边上都有一个字符
(或)，图上无自环无重边。
保证整张图是强连通的，也就是任意两点 \(s,t\) 间均至少存在一条 \(s\) 到 \(t\) 的路径。
问是否存在一条路径使得：
- 路径的起点与终点相同。
- 每条边至少在路径中被经过一次。
- 路径经过的边上的字符依次连接形成一个合法括号序列。
\(2 \leq N \leq 4000\)，\(N \leq M \leq 8000\)。
ABC077D
给定一个整数 \(K\)。求一个 \(K\) 的正整数倍 \(S\)，使得 \(S\) 的数位累加和最小。
CF1076D
给一个 \(n\) 个点，\(m\) 条边的无向简单带权连通图，要求删边至最多剩余 \(k\) 条边。
定义“好点”是指删边后，\(1\) 号节点到它的最短路长度仍然等于原图最短路长度的节点。
最大化删边后的好点个数。
CF1163F
给你一个 \(n\) 个点，\(m\) 条边的无向图，每条边连接点 \(u, v\)，并且有个长度 \(w\)。
有 \(q\) 次询问，每次询问给你一对 \(t, x\)，表示仅当前询问下，将 \(t\) 这条边的长度修改为 \(x\)，请你输出当前 \(1\) 到 \(n\) 的最短路长度。
P2505
C 国有 \(n\) 座城市，城市之间通过 \(m\) 条单向道路连接。一条路径被称为最短路，当且仅当不存在从它的起点到终点的另外一条路径总长度比它小。两条最短路不同，当且仅当它们包含的道路序列不同。我们需要对每条道路的重要性进行评估，评估方式为计算有多少条不同的最短路经过该道路。现在，这个任务交给了你。
AGC001F
给出一个元素集合为 \(\{1,2,\dots,N\}\) \((1\leq N\leq 500,000)\) 的排列 \(P\)，当有 \(i,j\) \((1\leq i<j\leq N)\) 满足 \(j-i\geq K\) \((1\leq K\leq N-1)\) 且 \(|P_{i}-P_{j}|=1\) 时，可以交换 \(P_{i}\) 和 \(P_{j}\)。
求：可能排列中字典序最小的排列。
P5960
给出一组包含 \(m\) 个不等式，有 \(n\) 个未知数的形如：
\[\begin{cases} x_{c_1}-x_{c'_1}\leq y_1 \\x_{c_2}-x_{c'_2} \leq y_2 \\ \cdots\\ x_{c_m} - x_{c'_m}\leq y_m\end{cases} \]的不等式组，求任意一组满足这个不等式组的解。
P4926
P3275
输入的第一行是两个整数 \(N\)，\(K\)。接下来 \(K\) 行，表示这些点需要满足的关系，每行 \(3\) 个数字，\(X\)，\(A\)，\(B\)。
- 如果 \(X=1\)， 表示第 \(A\) 个小朋友分到的糖果必须和第 \(B\) 个小朋友分到的糖果一样多；
- 如果 \(X=2\)， 表示第 \(A\) 个小朋友分到的糖果必须少于第 \(B\) 个小朋友分到的糖果；
- 如果 \(X=3\)， 表示第 \(A\) 个小朋友分到的糖果必须不少于第 \(B\) 个小朋友分到的糖果；
- 如果 \(X=4\)， 表示第 \(A\) 个小朋友分到的糖果必须多于第 \(B\) 个小朋友分到的糖果；
- 如果 \(X=5\)， 表示第 \(A\) 个小朋友分到的糖果必须不多于第 \(B\) 个小朋友分到的糖果；
P7515
Alice 有一个 \(n \times m\) 的矩阵 \(a_{i, j}\)（\(1 \le i \le n\)，\(1 \le j \le m\)），其每个元素为大小不超过 \({10}^6\) 的非负整数。
Bob 根据该矩阵生成了一个 \((n - 1) \times (m - 1)\) 的矩阵 \(b_{i, j}\)（\(1 \le i \le n - 1\)，\(1 \le j \le m - 1\)），每个元素的生成公式为\[b_{i, j} = a_{i, j} + a_{i, j + 1} + a_{i + 1, j} + a_{i + 1, j + 1} \]现在 Alice 忘记了矩阵 \(a_{i, j}\)，请你根据 Bob 给出的矩阵 \(b_{i, j}\) 还原出 \(a_{i, j}\)。
P2474
你有 \(n\) 个砝码，均为 \(1\) 克，\(2\) 克或者 \(3\) 克。你并不清楚每个砝码的重量，但你知道其中一些砝码重量的大小关系。你把其中两个砝码 A 和 B 放在天平的左边，需要另外选出两个砝码放在天平的右边。问：有多少种选法使得天平的左边重(\(c_1\))、一样重(\(c_2\))、右边重(\(c_3\))？（只有结果保证唯一确定的选法才统计在内）
第一行包含三个正整数 \(n\), \(A\), \(B\)（\(1\le A,B\le n\), \(A\neq B\)）。
以下 \(n\) 行包含重量关系矩阵，其中第 \(i\) 行第 \(j\) 个字符为加号+表示砝码 \(i\) 比砝码 \(j\) 重，减号-表示砝码 \(i\) 比砝码 \(j\) 轻，等号=表示砝码 \(i\) 和砝码 \(j\) 一样重，问号?表示二者的关系未知。
数据保证至少存在一种情况符合该矩阵。
\(n\le 50\)。
P3530
你不知道越野赛的结果，但 Byteasar 会告诉你部分信息。现在，他要你答出：所有参赛者最多能达到多少种不同的成绩，而不违背他给的条件。（他们中的一些人可能平局，也就是同时到达终点，这种情况只算有一种成绩）。
Byteasar 告诉你，所有参赛者的成绩都是整数秒。他还会为你提供了一些参赛者成绩的关系。具体是：他会给你一些数对 \((A, B)\)，表示 \(A\) 的成绩正好比 \(B\) 快 \(1\) 秒；他还会给你一些数对 \((C, D)\)，表示 \(C\) 的成绩不比 \(D\) 慢。而你要回答的是：所有参赛者最多能达到多少种不同的成绩，而不违背他给的条件。
请你编程解决这个谜题。
AGC004D · 贪心
有 \(n\) 个城市，每个城市有一个传送点，都可以传送到唯一的一个城市，保证从任何位置出发经过若干次传送之后能够到达 \(1\) 号城市。现在希望修改一些点的目的地，使得从任何一点出发在传送 \(K\) 次之后恰好都能到达 \(1\) 号城市，求最少要改变目的地的城市的数量。
注意到 \(1\) 一定要指向自己形成自环，因为这样就可以让点都到 \(1\) 这里转一转，直到 \(k\) 步为止。
现在就只剩下 \(n-1\) 条边了，成为了一棵树。
因为每个点到 \(1\) 步数要不小于 \(k\) 要不大于 \(k\)，而前者已经解决了，接下来只要对于大于 \(k\) 的情况分析即可。
我们将原树分成若干棵树，这几棵树的最大深度不超过 \(k-1\)。接下来就可以贪心了。
P4768
本题的故事发生在魔力之都，在这里我们将为你介绍一些必要的设定。
魔力之都可以抽象成一个 \(n\) 个节点、\(m\) 条边的无向连通图（节点的编号从 \(1\) 至 \(n\)）。我们依次用 \(l,a\) 描述一条边的长度、海拔。
作为季风气候的代表城市，魔力之都时常有雨水相伴，因此道路积水总是不可避免的。由于整个城市的排水系统连通，因此有积水的边一定是海拔相对最低的一些边。我们用水位线来描述降雨的程度，它的意义是：所有海拔不超过水位线的边都是有积水的。
Yazid 是一名来自魔力之都的 OIer，刚参加完 ION2018 的他将踏上归程，回到他温暖的家。Yazid 的家恰好在魔力之都的 \(1\) 号节点。对于接下来 \(Q\) 天，每一天 Yazid 都会告诉你他的出发点 \(v\) ，以及当天的水位线 \(p\)。
每一天，Yazid 在出发点都拥有一辆车。这辆车由于一些故障不能经过有积水的边。Yazid 可以在任意节点下车，这样接下来他就可以步行经过有积水的边。但车会被留在他下车的节点并不会再被使用。
需要特殊说明的是，第二天车会被重置，这意味着：
- 车会在新的出发点被准备好。
- Yazid 不能利用之前在某处停放的车。
Yazid 非常讨厌在雨天步行，因此他希望在完成回家这一目标的同时，最小化他步行经过的边的总长度。请你帮助 Yazid 进行计算。
本题的部分测试点将强制在线，具体细节请见【输入格式】和【子任务】。
B3609 · 强连通分量模板
给定一张 \(n\) 个点 \(m\) 条边的有向图，求出其所有的强连通分量。
注意，本题可能存在重边和自环。
输出格式：
第一行一个整数表示这张图的强连通分量数目。
接下来每行输出一个强连通分量。第一行输出 1 号点所在强连通分量，第二行输出 2 号点所在强连通分量，若已被输出，则改为输出 3 号点所在强连通分量，以此类推。每个强连通分量按节点编号大小输出。
点击查看代码
int n,m;
struct node
{
int to,nxt;
}e[200001];
int gcnt,head[200001];
void add(int u,int v)
{
e[++gcnt].to = v;
e[gcnt].nxt = head[u];
head[u] = gcnt;
}
stack<int> st;
bool vis[200001];
int dfn[200001],low[200001],ans[200001];
int cnt;
int SCG;
vector<int> bel[200001];
void tarjan(int u)
{
cnt++;
dfn[u] = low[u] = cnt;
st.push(u);
vis[u] = 1;
int i;
for(i=head[u];i;i=e[i].nxt)
{
int v = e[i].to;
if(!dfn[v])
{
tarjan(v);
low[u] = min(low[u],low[v]);
}
else if(vis[v])
low[u] = min(low[u],dfn[v]);
}
if(dfn[u]==low[u])
{
SCG++;
int x;
do
{
x = st.top();
st.pop();
vis[x] = 0;
bel[SCG].push_back(x);
ans[x] = SCG;
}while(x!=u);
}
}
bool f[200001];
void solve()
{
cin>>n>>m;
int i;
for(i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
}
for(i=1;i<=n;i++)
if(!dfn[i])
tarjan(i);
cout<<SCG<<endl;
for(i=1;i<=SCG;i++)
sort(bel[i].begin(),bel[i].end());
for(i=1;i<=n;i++)
{
if(f[ans[i]])
continue;
f[ans[i]] = 1;
int j;
for(j=0;j<bel[ans[i]].size();j++)
cout<<bel[ans[i]][j]<<' ';
cout<<endl;
}
return;
}
P2341 · 缩点
每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 \(A\) 喜欢 \(B\)，\(B\) 喜欢 \(C\)，那么 \(A\) 也喜欢 \(C\)。牛栏里共有 \(N\) 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。
注意到喜欢是传递关系，因此考虑缩点。
缩点后的奶牛就不会相互有喜欢的关系了，因此只有不喜欢他人的牛才有可能当明星。如果只有一个出度为 \(0\) 的点，那么明星牛的个数就是那个强连通分量所包含的点的个数，如果有多个出度为 \(0\) 的点，那么明星牛的个数就为 \(0\)。
P2272
一个有向图 \(G=\left(V,E\right)\) 称为半连通的 (Semi-Connected)，如果满足：\(\forall u,v\in V\)，满足 \(u\to v\) 或 \(v\to u\)，即对于图中任意两点 \(u,v\)，存在一条 \(u\) 到 \(v\) 的有向路径或者从 \(v\) 到 \(u\) 的有向路径。
若 \(G'=\left(V',E'\right)\) 满足 \(V'\subseteq V\)，\(E'\) 是 \(E\) 中所有跟 \(V'\) 有关的边，则称 \(G'\) 是 \(G\) 的一个导出子图。若 \(G'\) 是 \(G\) 的导出子图，且 \(G'\) 半连通，则称 \(G'\) 为 \(G\) 的半连通子图。若 \(G'\) 是 \(G\) 所有半连通子图中包含节点数最多的，则称 \(G'\) 是 \(G\) 的最大半连通子图。
给定一个有向图 \(G\)，请求出 \(G\) 的最大半连通子图拥有的节点数 \(K\)，以及不同的最大半连通子图的数目 \(C\)。由于 \(C\) 可能比较大，仅要求输出 \(C\) 对 \(X\) 的余数。
CF1239D
有 \(n\) 个人和 \(n\) 只猫，人和猫都以 \(1\sim n\) 编号，第 \(i\) 个人是第 \(i\) 只猫的主人。每个人都认识一些猫（其中包括自己的猫）。
要求选出 \(j\) 名裁判（人）和 \(p\) 只选手（猫），使得 \(j+p=n\)，且 \(1<j,p<n\)，且选出的任何人都不认识任何一只猫。
如果不存在这样的方案输出一行No。
如果存在则第一行输出Yes，第二行输出两个数字分别代表裁判和选手的数量，第三行输出所有裁判的编号，第四行输出所有选手的编号。
ARC092F
- 有一个 \(N\) 个点 \(M\) 条边的有向图。保证图中不存在重边和自环。
- 试判断将每条边反向，其他边不变的情况下，图中强连通分量的数量是否改变。
- 若改变，输出
diff，否则输出same。- \(1 \leq N \leq 10^3\)，\(1 \leq M \leq 2 \times 10^5\)。
UOJ134
CF1142E
给定一张 \(n\) 个点的竞赛图。边分为粉色和绿色。粉色的边有 \(m\) 条，你已经知道了它们的方向。而绿色的边你不知道方向。
每次询问，你可以获得一条绿色的边的方向。
你需要在 \(2n\) 次询问内，找到一个点 \(u\)，使得对于每个点 \(v\)，都有一条 \(u\to v\) 的路径，使得路径上每条边同色。需要注意的是路径只能通过粉边和你已经询问的绿边。
交互库是自适应的。
\(n, m \leq 10^5\)。
P3388 · 割点
给出一个 \(n\) 个点，\(m\) 条边的无向图，求图的割点。
点击查看代码
struct node
{
int to,nxt;
}e[200001];
int head[200001],gcnt;
void add(int u,int v)
{
gcnt++;
e[gcnt].to = v;
e[gcnt].nxt = head[u];
head[u] = gcnt;
}
int n,m;
int dfn[200001],low[200001];
int clk;
bool cut[200001];
int rt;
void tarjan(int u)
{
int point = 0;
clk++;
dfn[u] = low[u] = clk;
int i;
for(i=head[u];i;i=e[i].nxt)
{
int v = e[i].to;
if(!dfn[v])
{
tarjan(v);
low[u] = min(low[u],low[v]);
if(low[v]>=dfn[u])
{
point++;
if(u!=rt||point>1)
cut[u] = 1;
}
}
else
low[u] = min(low[u],dfn[v]);
}
return;
}
void solve()
{
cin>>n>>m;
int i;
for(i=1;i<=m;i++)
{
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
for(i=1;i<=n;i++)
if(!dfn[i])
rt = i,tarjan(i);
int ans = 0;
for(i=1;i<=n;i++)
if(cut[i])
ans++;
cout<<ans<<endl;
for(i=1;i<=n;i++)
if(cut[i])
cout<<i<<' ';
return;
}
UOJ67
P3225
煤矿工地可以看成是由隧道连接挖煤点组成的无向图。为安全起见，希望在工地发生事故时所有挖煤点的工人都能有一条出路逃到救援出口处。于是矿主决定在某些挖煤点设立救援出口，使得无论哪一个挖煤点坍塌之后，其他挖煤点的工人都有一条道路通向救援出口。
请写一个程序，用来计算至少需要设置几个救援出口，以及不同最少救援出口的设置方案总数。
P1173 · 割点
跳蚤国王和蛐蛐国王在玩一个游戏。
他们在一个 \(n\) 行 \(m\) 列的网格上排兵布阵。其中的 \(c\) 个格子中 \((0 \leq c \leq n\cdot m)\)，每个格子有一只蛐蛐，其余的格子中，每个格子有一只跳蚤。
我们称占据的格子有公共边的两只跳蚤是相邻的。
我们称两只跳蚤是连通的，当且仅当这两只跳蚤相邻，或存在另一只跳蚤与这两只跳蚤都连通。
现在，蛐蛐国王希望，将某些（零个，一个或多个）跳蚤替换成蛐蛐，使得在此之后存在至少两只跳蚤不连通。
例如：图 \(1\) 描述了一个 \(n=4\)，\(m=4\)，\(c=2\) 的情况。
这种情况下蛐蛐国王可以通过将第二行第二列，和第三行第三列的两只跳蚤替换为蛐蛐，从而达成他的希望，如右图所示。并且，不存在更优的方案，但是可能存在其他替换两只跳蚤的方案。
你需要首先判断蛐蛐国王的希望能否被达成。如果能够达成，你还需要最小化被替换的跳蚤的个数。
纪念第一道独立想出来的黑题。
显然答案为 \(0,-1,1,2\) 的其中之一。因为我们最多用两个跳蚤，就可以让最上面一行，最靠边的一个跳蚤和其他的不连通。读者自己画图很容易理解。
所以你可以随机输出这四个数中的任意一个，正确率高达 \(\dfrac{1}{4^T}\)。
对于每种情况分别考虑。
- 答案为 \(-1\)
若只剩下一个格子，或剩下的两个格子是相邻的，那么答案显然为 \(-1\)，因为不论放不放蛐蛐，都不能使这剩下的跳蚤分开。
- 答案为 \(0\)
若原图有两个跳蚤都不在一个 \(8\) 连通块内，那么答案就是 \(0\)。但我们不能直接通过 bfs 计算，因为无效的跳蚤太多了。既然有这么多没用的跳蚤，那就从中挑几个有用的呗。
考虑对于每一个蛐蛐的周围的八个跳蚤都拿出来，看看每个蛐蛐 \(4\) 连通块周围的跳蚤是否都在同一个连通块内即可。
例如下图，跳蚤是黄色（没上色的也是跳蚤），蛐蛐是红色。两个蛐蛐 \(4\) 连通块将跳蚤分成 \(2\) 部分。注意左边那一部分，这个 \(4\) 连通块旁边的跳蚤不属于一个连通块，此时答案是 \(0\)。
- 答案为 \(1\)
接下来考虑答案为 \(1\) 的情况。
我们仍然取出每个蛐蛐周围的 \(8\) 个跳蚤，如果存在一个跳蚤，把它变成蛐蛐后，原来和它相邻的跳蚤会分成若干连通块，那么答案就是 \(1\) 了。显然这个跳蚤也是一个割点。
可是，这么做一定是正确的吗？其实并不对，下图就是一个反例。
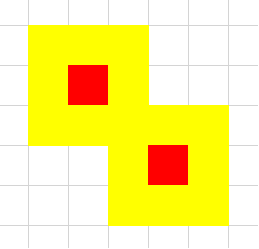
如果按照上述的方法，求得的割点其实是黄色八字形的中间那个点。但是若将这个点标记为蛐蛐，会发现它只会让这个点周围的跳蚤不联通，实际上，这些跳蚤可以通过它们周围的跳蚤联通。
为了解决这个问题，我们只需要将蛐蛐周围的跳蚤的跳蚤也拿出来，这样再求出割点（必须是蛐蛐周围的），也就是真的割点了。例如下图。
- 答案为 \(2\)
除去以上三种情况，其他情况直接输出 \(2\) 即可。
P8436
P2783
HDOJ2460
HDOJ7334
CF555E
- 给定一张 \(n\) 个点 \(m\) 条边的无向图。
- 给定 \(q\) 组有向点对 \((s, t)\)。
- 询问是否存在使得所有 \(s\) 都能到达 \(t\) 的无向图中每条边的定向方案。
- \(n,m,q \le 2 \times 10^5\)。
CF786B
P5025
在一条直线上有 \(n\) 个炸弹，每个炸弹的坐标是 $ x_i $，爆炸半径是 $ r_i $，当一个炸弹爆炸时，如果另一个炸弹所在位置 $ x_j $ 满足：
$ |x_j-x_i| \le r_i $ ，那么，该炸弹也会被引爆。
现在，请你帮忙计算一下，先把第 \(i\) 个炸弹引爆，将引爆多少个炸弹呢？
答案对 \(10^9 + 7\) 取模。
P3588
给定一个长度为 \(n\) 的正整数序列 \(a\)，每个数都在 \(1\) 到 \(10^9\) 范围内，告诉你其中 \(s\) 个数，并给出 \(m\) 条信息，每条信息包含三个数 \(l,r,k\) 以及接下来 \(k\) 个正整数，表示 \(a_l, a_{l+1}, \ldots, a_{r-1}, a_r\) 里这 \(k\) 个数中的任意一个都比任意一个剩下的 \(r-l+1-k\) 个数大（严格大于，即没有等号）。
请任意构造出一组满足条件的方案，或者判断无解。
P8867
A 国与 B 国正在激烈交战中，A 国打算在自己的国土上建造一些军营。
A 国的国土由 \(n\) 座城市组成，\(m\) 条双向道路连接这些城市，使得任意两座城市均可通过道路直接或间接到达。A 国打算选择一座或多座城市（至少一座），并在这些城市上各建造一座军营。
众所周知，军营之间的联络是十分重要的。然而此时 A 国接到情报，B 国将会于不久后袭击 A 国的一条道路，但具体的袭击目标却无从得知。如果 B 国袭击成功，这条道路将被切断，可能会造成 A 国某两个军营无法互相到达，这是 A 国极力避免的。因此 A 国决定派兵看守若干条道路（可以是一条或多条，也可以一条也不看守)，A 国有信心保证被派兵看守的道路能够抵御 B 国的袭击而不被切断。
A 国希望制定一个建造军营和看守道路的方案，使得 B 国袭击的无论是 A 国的哪条道路，都不会造成某两座军营无法互相到达。现在，请你帮 A 国计算一下可能的建造军营和看守道路的方案数共有多少。由于方案数可能会很多，你只需要输出其对 \(1,000,000,007\left(10^{9}+7\right)\) 取模的值即可。两个方案被认为是不同的，当且仅当存在至少一 座城市在一个方案中建造了军营而在另一个方案中没有，或者存在至少一条道路在一个 方案中被派兵看守而在另一个方案中没有。
P5058
某军搞信息对抗实战演习，红军成功地侵入了蓝军的内部网络。
蓝军共有两个信息中心，红军计划在某台中间服务器上安装一个嗅探器，从而能够侦听到两个信息中心互相交换的所有信息。
但是蓝军的网络相当的庞大，数据包从一个信息中心传到另一个信息中心可以不止有一条通路。
现在需要你尽快地解决这个问题，应该把嗅探器安装在哪个中间服务器上才能保证所有的数据包都能被捕获？
P8435 · 点双/圆方树
对于一个 \(n\) 个节点 \(m\) 条无向边的图，请输出其点双连通分量的个数，并且输出每个点双连通分量。
P4320
在 H 国的小 w 决定到从城市 \(u\) 到城市 \(v\) 旅行，但是此时小 c 由于各种原因不在城市 \(u\)，但是小 c 决定到在中途与小 w 相遇。
由于 H 国道路的原因，小 w 从城市 \(u\) 到城市 \(v\) 的路线不是固定的，为了合理分配时间，小 c 想知道从城市 \(u\) 到城市 \(v\) 有多少个城市小 w 一定会经过，特别地，\(u, v\) 也必须被算进去，也就是说无论如何答案不会小于 2。
由于各种特殊的原因，小 c 并不知道小 w 的起点和终点，但是小 c 知道小 w 的起点和终点只有 \(q\) 种可能，所以对于这 \(q\) 种可能，小 c 都想知道小 w 一定会经过的城市数。
H 国所有的边都是无向边，两个城市之间最多只有一条道路直接相连，没有一条道路连接相同的一个城市。
任何时候，H 国不存在城市 \(u\) 和城市 \(v\) 满足从 \(u\) 无法到达 \(v\)。
P4606
省选临近，放飞自我的小 Q 无心刷题，于是怂恿小 C 和他一起颓废，玩起了一款战略游戏。
这款战略游戏的地图由 \(n\) 个城市以及 \(m\) 条连接这些城市的双向道路构成，并且从任意一个城市出发总能沿着道路走到任意其他城市。
现在小 C 已经占领了其中至少两个城市，小 Q 可以摧毁一个小 C 没占领的城市，同时摧毁所有连接这个城市的道路。只要在摧毁这个城市之后能够找到某两个小 C 占领的城市 \(u\) 和 \(v\)，使得从 \(u\) 出发沿着道路无论如何都不能走到 \(v\)，那么小 Q 就能赢下这一局游戏。
小 Q 和小 C 一共进行了 \(q\) 局游戏，每一局游戏会给出小 C 占领的城市集合 \(S\)，你需要帮小 Q 数出有多少个城市在他摧毁之后能够让他赢下这一局游戏。
SP2878
有 \(n\) 个骑士经常举行圆桌会议，商讨大事。每次圆桌会议至少有 \(3\) 个骑士参加，且相互憎恨的骑士不能坐在圆桌的相邻位置。如果发生意见分歧，则需要举手表决，因此参加会议的骑士数目必须是大于 \(1\) 的奇数，以防止赞同和反对票一样多。知道骑士之间相互憎恨的关系后，请你帮忙统计有多少骑士参加不了任意一个会议。
CF487E
Cyberland 有 \(n\) 座城市，编号从 \(1\) 到 \(n\)，有 \(m\) 条双向道路连接这些城市。第 \(j\) 条路连接城市 \(a_j\) 和 \(b_j\)。每天，都有成千上万的游客来到 Cyberland 游玩。
在每一个城市，都有纪念品售卖，第 \(i\) 个城市售价为 \(w_i\)。这个售价有时会变动。
每一个游客的游览路径都有固定起始城市和终止城市，且不会经过重复的城市。
他们会在路径上的城市中，售价最低的那个城市购买纪念品。
你能求出每一个游客在所有合法的路径中能购买的最低售价是多少吗？
你要处理 \(q\) 个操作：
C a w： 表示 \(a\) 城市的纪念品售价变成 \(w\)。
A a b： 表示有一个游客要从 \(a\) 城市到 \(b\) 城市，你要回答在所有他的旅行路径中最低售价的最低可能值。
P5236
给你一个有 \(n\) 个点和 \(m\) 条边的仙人掌图（任意一条边至多只出现在一条简单回路的无向连通图称为仙人掌），和 \(q\) 组询问
每次询问两个点 \(u,v\)，求两点之间的最短路。
保证输入数据没有重边。
P7025
给定一张 \(n\) 个节点 \(m\) 条边的无向图，请在图中找出两个点 \(S\) 和 \(F\)，使得这两点间至少存在三条不相交的路径。
P4782 · 2-SAT
有 \(n\) 个布尔变量 \(x_1\)\(\sim\)\(x_n\)，另有 \(m\) 个需要满足的条件，每个条件的形式都是 「\(x_i\) 为
true/false或 \(x_j\) 为true/false」。比如 「\(x_1\) 为真或 \(x_3\) 为假」、「\(x_7\) 为假或 \(x_2\) 为假」。
2-SAT 问题的目标是给每个变量赋值使得所有条件得到满足。
点击查看代码
struct node
{
int to,nxt;
}e[2000001];
int gcnt,head[2000001];
void add(int u,int v)
{
gcnt++;
e[gcnt].to = v;
e[gcnt].nxt = head[u];
head[u] = gcnt;
}
int n,m;
stack<int> st;
int dfn[2000001],low[2000001];
int clk;
bool vis[2000001];
int SCG;
int id[2000001];
void tarjan(int u)
{
st.push(u);
clk++;
vis[u] = 1;
dfn[u] = low[u] = clk;
int i;
for(i=head[u];i;i=e[i].nxt)
{
int v = e[i].to;
if(!dfn[v])
{
tarjan(v);
low[u] = min(low[u],low[v]);
}
else if(vis[v])
low[u] = min(low[u],dfn[v]);
}
if(low[u]==dfn[u])
{
int x;
SCG++;
do
{
x = st.top();
st.pop();
vis[x] = 0;
id[x] = SCG;
}while(x!=u);
}
}
void solve()
{
cin>>n>>m;
int i;
for(i=1;i<=m;i++)
{
int a,x,b,y;
cin>>x>>a>>y>>b;
add(x+a*n,y+(!b)*n);
add(y+b*n,x+(!a)*n);
}
for(i=1;i<=2*n;i++)
if(!dfn[i])
tarjan(i);
for(i=1;i<=n;i++)
if(id[i]==id[i+n])
{
cout<<"IMPOSSIBLE"<<endl;
return;
}
cout<<"POSSIBLE"<<endl;
for(i=1;i<=n;i++)
{
int x = (id[i]<=id[i+n]);
cout<<x<<' ';
}
cout<<endl;
return;
}
P5782
根据宪法，Byteland 民主共和国的公众和平委员会应该在国会中通过立法程序来创立。 不幸的是，由于某些党派代表之间的不和睦而使得这件事存在障碍。 此委员会必须满足下列条件：
- 每个党派都在委员会中恰有 \(1\) 个代表。
- 如果 \(2\) 个代表彼此厌恶，则他们不能都属于委员会。
每个党在议会中有 \(2\) 个代表。代表从 \(1\) 编号到 \(2n\)。 编号为 \(2i-1\) 和 \(2i\) 的代表属于第 \(i\) 个党派。
任务：写一程序读入党派的数量和关系不友好的代表对，计算决定建立和平委员会是否可能，若行，则列出委员会的成员表。
P4171
满汉全席是中国最丰盛的宴客菜肴，有许多种不同的材料透过满族或是汉族的料理方式，呈现在数量繁多的菜色之中。由于菜色众多而繁杂，只有极少数博学多闻技艺高超的厨师能够做出满汉全席，而能够烹饪出经过专家认证的满汉全席，也是中国厨师最大的荣誉之一。世界满汉全席协会是由能够料理满汉全席的专家厨师们所组成，而他们之间还细分为许多不同等级的厨师。
为了招收新进的厨师进入世界满汉全席协会，将于近日举办满汉全席大赛，协会派遣许多会员当作评审员，为的就是要在参赛的厨师之中，找到满汉界的明日之星。
大会的规则如下：每位参赛的选手可以得到 \(n\) 种材料，选手可以自由选择用满式或是汉式料理将材料当成菜肴。
大会的评审制度是：共有 \(m\) 位评审员分别把关。每一位评审员对于满汉全席有各自独特的见解，但基本见解是，要有两样菜色作为满汉全席的标志。如某评审认为，如果没有汉式东坡肉跟满式的涮羊肉锅，就不能算是满汉全席。但避免过于有主见的审核，大会规定一个评审员除非是在认为必备的两样菜色都没有做出来的状况下，才能淘汰一位选手，否则不能淘汰一位选手。
换句话说，只要参赛者能在这两种材料的做法中，其中一个符合评审的喜好即可通过该评审的审查。如材料有猪肉，羊肉和牛肉时，有四位评审员的喜好如下表：评审一 评审二 评审三 评审四 满式牛肉 满式猪肉 汉式牛肉 汉式牛肉 汉式猪肉 满式羊肉 汉式猪肉 满式羊肉如参赛者甲做出满式猪肉，满式羊肉和满式牛肉料理，他将无法满足评审三的要求，无法通过评审。而参赛者乙做出汉式猪肉，满式羊肉和满式牛肉料理，就可以满足所有评审的要求。
但大会后来发现，在这样的制度下如果材料选择跟派出的评审员没有特别安排好的话，所有的参赛者最多只能通过部分评审员的审查而不是全部，所以可能会发生没有人通过考核的情形。
如有四个评审员喜好如下表时，则不论参赛者采取什么样的做法，都不可能通过所有评审的考核：评审一 评审二 评审三 评审四 满式羊肉 满式猪肉 汉式羊肉 汉式羊肉 汉式猪肉 满式羊肉 汉式猪肉 满式猪肉所以大会希望有人能写一个程序来判断，所选出的 \(m\) 位评审，会不会发生没有人能通过考核的窘境，以便协会组织合适的评审团。
P6378
\(n\) 个点 \(m\) 条边的无向图被分成 \(k\) 个部分。每个部分包含一些点。
请选择一些关键点，使得每个部分恰有一个关键点，且每条边至少有一个端点是关键点。
P3825
小 L 计划进行 \(n\) 场游戏，每场游戏使用一张地图，小 L 会选择一辆车在该地图上完成游戏。
小 L 的赛车有三辆，分别用大写字母 \(A\)、\(B\)、\(C\) 表示。地图一共有四种，分别用小写字母 \(x\)、\(a\)、\(b\)、\(c\) 表示。
其中，赛车 \(A\) 不适合在地图 \(a\) 上使用，赛车 \(B\) 不适合在地图 \(b\) 上使用，赛车 \(C\) 不适合在地图 \(c\) 上使用，而地图 \(x\) 则适合所有赛车参加。
适合所有赛车参加的地图并不多见，最多只会有 \(d\) 张。
\(n\) 场游戏的地图可以用一个小写字母组成的字符串描述。例如：\(S=\texttt{xaabxcbc}\) 表示小 L 计划进行 \(8\) 场游戏，其中第 \(1\) 场和第 \(5\) 场的地图类型是 \(x\)，适合所有赛车，第 \(2\) 场和第 \(3\) 场的地图是 \(a\)，不适合赛车 \(A\)，第 \(4\) 场和第 \(7\) 场的地图是 \(b\)，不适合赛车 \(B\)，第 \(6\) 场和第 \(8\) 场的地图是 \(c\)，不适合赛车 \(C\)。
小 L 对游戏有一些特殊的要求，这些要求可以用四元组 $ (i, h_i, j, h_j) $ 来描述，表示若在第 \(i\) 场使用型号为 \(h_i\) 的车子，则第 \(j\) 场游戏要使用型号为 \(h_j\) 的车子。
你能帮小 L 选择每场游戏使用的赛车吗？如果有多种方案，输出任意一种方案。
如果无解，输出-1。
CF1215F
有 \(p\) 种电站，需要选择一种电站序列使其满足：
- \(n\) 对 \((x,y)\)，\(x\) 电站或 \(y\) 电站中至少有一个
- \(m\) 对 \((x,y)\)，\(x\) 电站或 \(y\) 电站中最多有一个
- 第 \(i\) 种电站有两个参数 \(li\) 和 \(ri\) \((1<=li<=ri<=M)\)，表示其覆盖的区间为\([li,ri]\)。若选定一个电站序列，序列中所有电站覆盖区间的交集不能为空。要求若求得一种合法电站序列，输出交集中任意一个点。
CF587D
给定一张 \(n\) 个点 \(m\) 条边的无向图，每条边有一个颜色 \(c\) 和权值 \(t\)。
你要选出一些边，使得它们是一个匹配，同时剩下的边每种颜色也是一个匹配。
同时，你要最小化选出的边的最大权值。
\(n,m \le 5 \times 10^4\)。
