平邑集训（补题）
Day 1
A 咕咕
题目描述
解法
DP，设 \(dp_{i,j}\) 表示从 \((1,1)\) 走到 \((n,m)\) 的方案数。
转移的时候，需要按照给定的限制走，如果一个点的（2）（3）限制冲突了，那么就标记一下，经过他的时候绕过他，时间复杂度 \(O(nm)\)。
代码
点击查看代码
int n,m,t;
int f[3001][3001];
int dp[3001][3001];
void solve()
{
cin>>n>>m>>t;
int i,j;
while(t--)
{
int a,b,c,d;
cin>>a>>b>>c>>d;
bool flag = 0;
if(a==n&&b==m)
continue;
if((c==a+1&&d==b)||(d==b+1&&a==c))
flag = 1;
if(!flag||f[a][b]==-1)
{
f[a][b] = -1;
continue;
}
if(c==a+1)
{
if(f[a][b]==2)
f[a][b] = -1;
else
f[a][b] = 1;
}
else if(d==b+1)
{
if(f[a][b]==1)
f[a][b] = -1;
else
f[a][b] = 2;
}
}
if(f[1][1]==-1)
{
cout<<0<<endl;
return;
}
dp[1][1] = 1;
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
if(f[i][j]==-1)
dp[i][j]=0;
else
{
if(f[i-1][j]!=2)
dp[i][j] += dp[i-1][j];
if(f[i][j-1]!=1)
dp[i][j] += dp[i][j-1];
dp[i][j] %= mod;
}
}
cout<<dp[n][m]<<endl;
return;
}
B 找子串
题目描述
解法
- Subtask 1
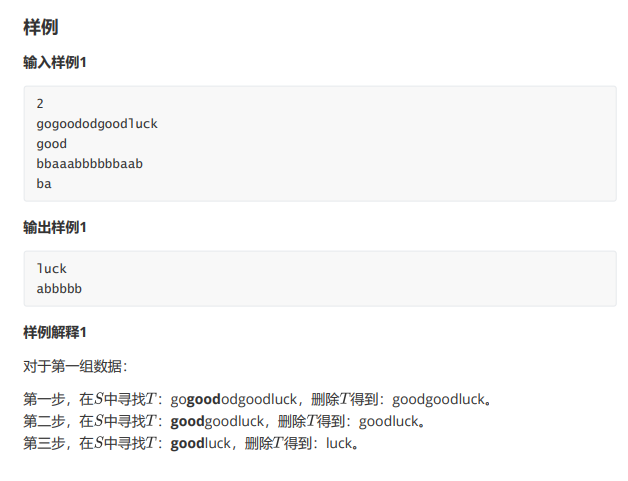
每次删掉 \(T\) 后重新暴力再找第一个 \(T\)，时间复杂度 \(O(\dfrac{|S|}{|T|}\cdot |S| \cdot |T|)\)。
- Subtask 2
每次删掉 \(T\) 后用 kmp 或哈希找到第一个 \(T\)，时间复杂度 \(O(\dfrac{|S|}{|T|}\cdot |S|)\)。
- Subtask 3
每次删掉 \(T\) 后，从删掉位置之前的 \(T\) 个位置开始，用 kmp 或哈希找 \(T\)，时间复杂度 \(O(|S|\cdot |T|)\)。
- 满分做法
用 kmp 从 \(S\) 中找 \(T\) 时，对于 \(S\) 中的每一个位置 \(i\)，记录以 \(i\) 为结尾的子串，和 \(T\) 最多匹配到哪里，可以用一个数组记录下来，比如 \(match\)。
举个例子：若 \(S="gogoododgoodluck",T="good"\).
则 \(match_0 = 0\)，因为 \(S\) 中的 g 与 \(T\) 中的 g 匹配。
则 \(match_1 = 1\)，因为 \(S\) 中的 go 与 \(T\) 中的 go 匹配。
则 \(match_2 = 0\)，因为 \(S\) 中的 g 与 \(T\) 中的 g 匹配。
则 \(match_3 = 1\)，因为 \(S\) 中的 go 与 \(T\) 中的 go 匹配。
则 \(match_4 = 2\)，因为 \(S\) 中的 goo 与 \(T\) 中的 goo 匹配。
则 \(match_5 = 3\)，因为 \(S\) 中的 good 与 \(T\) 中的 good 匹配。
在上面的例子中，如果将第一个 good 从 \(S\) 中删除后，没有必要从头开始找 good，因为以前就知道 \(match_1=1\)，因此从 \(S_1\) 处继续 kmp 即可，可以通过栈来实现。
代码
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e6 + 7;
char s[maxn], t[maxn];
char sta[maxn];
int fail[maxn], fail1[maxn], n, m, top;
void init()
{
for (int i = 2, j = 0; i <= m; i++)
{
while (j && t[i] != t[j + 1])
{
j = fail[j];
}
if (t[i] == t[j + 1])
j++;
fail[i] = j;
}
}
void kmp()
{
for (int i = 1, j = 0; i <= n; i++)
{
sta[++top] = s[i];
while (j && sta[top] != t[j + 1])
{
j = fail[j];
}
if (sta[top] == t[j + 1])
j++;
fail1[top] = j;
if (j == m)
{
top -= m;
j = fail1[top];
}
}
}
int main()
{
scanf("%s", s + 1);
scanf("%s", t + 1);
n = strlen(s + 1);
m = strlen(t + 1);
init();
kmp();
for (int i = 1; i <= top; i++)
printf("%c", sta[i]);
return 0;
}
C LCS 问题
题目描述
思路
- 对于前 \(60\%\) 的数据
因为序列长度最多为 \(5000\)，所以可以暴力 LCS。考虑 dp，\(f_{i,j}\) 表示 \(a\) 数组前 \(i\) 个数和 \(b\) 数组前 \(i\) 个数的最长公共子序列。
如果 \(a_i=b_j\)，那么 \(f_{i,j} = max(f_{i-1,j},f_{i,j-1},f_{i-1,j-1}+1)\)。
然后 \(f_{i,j}=max(f_{i-1,j},f_{i,j-1})\)。
时间复杂度为 \(O(n^2)\)。
- 满分做法
关键在于保证 \(1~n\) 这 \(n\) 个数在 \(a,b\) 中分别出现 \(5\) 次。枚举 \(i\)，同时维护 \(f_j\) 表示 \(a\) 数组前 \(i\) 个数和 \(b\) 数组前 \(j\) 个数的最长公共子序列。同时要求这个最长公共子序列在 \(b\) 中必须以 \(b_j\) 结尾。
一开始对于每个 \(x\)，用二维数组存下数值 \(x\) 在 \(b\) 中的所有位置。枚举 \(i\) 时，枚举数值 \(a_i\) 在 \(b\) 中的所有位置 \(k\)。这时候所有的 \(f_j\) 都是 \(a\) 数组中前 \(i\) 个数和 \(b\) 数组中前 \(j\) 个数的最长公共子序列。
我们令 \(g_k = \max_{i=1}^{k-1} f_i+1\)，那么 \(g_k\) 也就是 \(a\) 数组中前 \(i\) 个数和 \(b\) 数组中前 \(k\) 个数的最长公共子序列。
对于 \(b_j \ne a_i\) 的 \(j\)，显然 \(g_j=f_j\)，也就是说 \(f_j\) 不用改动。
那么我们现在就要单点修改，求前缀最大值，用树状数组维护 \(f_j\) 的前缀最大值，时间复杂度 \(O(nlogn)\)。
代码
点击查看代码
inline int lowbit(int x)
{
return x&(-x);
}
inline void change(int x,int y)
{
for(int i=x;i<=N;i+=lowbit(i))
f[i]=max(f[i],y);
return;
}
inline int query(int x)
{
int res=0;
for(int i=x;i;i-=lowbit(i))
res=max(f[i],res);
return res;
}
for(int i=1;i<=n5;i++)
{
int x=read();
c[x][++cnt[x]]=i;
}
for(int i=1;i<=n5;i++)b[i]=read();
for(int i=1;i<=n*5;i++)
for(int j=5;j;j--)
{
int res=query(c[b[i]][j]-1);
change(c[b[i]][j],res+1);
D 舞步
题目描述
Farmer John 的奶牛们正在炫耀她们的最新舞步！
最初，所有的 \(N\) 头奶牛（\(2≤N≤10^5\)）站成一行，奶牛 \(i\) 排在其中第 \(i\) 位。舞步序列给定为 \(K\) （\(1≤K≤2\times10^5\)）个位置对 \((a_1,b_1),(a_2,b_2),…,(a_K,b_K)\)。在舞蹈的第 \(i=1…K\) 分钟，位置 \(a_i\) 与 \(b_i\) 上的奶牛交换位置。同样的 \(K\) 次交换在第 \(K+1…2K\) 分钟发生，在第 \(2K+1…3K\) 分钟再次发生，以此类推，周期性地持续共 \(M\) 分钟（\(1≤M≤10^{18}\)）。换言之，
- 在第 \(1\) 分钟，位置 \(a_1\) 与 \(b_1\) 上的奶牛交换位置。
- 在第 \(2\) 分钟，位置 \(a_2\) 与 \(b_2\) 上的奶牛交换位置。
- ……
- 在第 \(K\) 分钟，位置 \(a_K\) 与 \(b_K\) 上的奶牛交换位置。
- 在第 \(K+1\) 分钟，位置 \(a_1\) 与 \(b_1\) 上的奶牛交换位置。
- 在第 \(K+2\) 分钟，位置 \(a_2\) 与 \(b_2\) 上的奶牛交换位置。
- 以此类推……
对于每头奶牛，求她在队伍中会占据的不同的位置数量。
注意：本题每个测试点的时间限制为默认限制的两倍。
输入格式
输入的第一行包含 \(N\)、\(K\) 和 \(M\)。以下 \(K\) 行分别包含 \((a_1,b_1)…(a_K,b_K)\)（\(1≤a_i<b_i≤N\)）。
输出格式
输出 \(N\) 行，第 \(i\) 行包含奶牛 \(i\) 可以到达的不同的位置数量。
提示
\(7\) 分钟之后，各个位置上的奶牛为 \([3,4,5,2,1,6]\)。
- 奶牛 \(1\) 可以到达位置 \(\{1,2,3,4,5\}\)。
- 奶牛 \(2\) 可以到达位置 \(\{1,2,3,4\}\)。
- 奶牛 \(3\) 可以到达位置 \(\{1,2,3\}\)。
- 奶牛 \(4\) 可以到达位置 \(\{2,3,4\}\)。
- 奶牛 \(5\) 可以到达位置 \(\{3,4,5\}\)。
- 奶牛 \(6\) 从未移动，所以她没有离开过位置 \(6\)。
测试点性质：
- 测试点 1-5 满足 \(N≤100,K≤200\)。
- 测试点 6-10 满足 \(M=10^{18}\)。
- 测试点 11-20 没有额外限制。
我们先考虑弱化版，即将 周期性地持续共 M 分钟 改为 无限循环。
弱化版
考虑经过 \(k\) 分钟后，每头牛会途径某些点到达另一个点，假如 \(A\) 从 \(x\) 位置走到了 \(y\) 位置，\(B\) 从 \(x\) 走到了 \(x\)，那么再经过一轮，\(B\) 也会走到 \(y\) 位置。
也就是说 \(B\) 的运动轨迹会和 \(A\) 一样，只不过落后 \(k\) 分钟罢了。同时 \(B\) 经过的点也和 \(A\) 一样，所以像 \(A,B\) 一样的有相同运动轨迹的牛，它们的运动轨迹将会在 \(k\) 分钟之内构成一个环。
而环可以用并查集维护。接下来用 vector 记录每个点经过的点，对于一个环内的牛，用 set 统计每个点经过了多少个点，设为 \(x\)，则环内每一个牛能经过的点数也就是 \(x\)。
时间复杂度 \(O(n+k)\)。
普通版
也就是多了个时间限制。
令 \(times = \left \lfloor \dfrac{m}{k} \right \rfloor\) 表示一个点开始走会完整走 \(t\) 轮，\(w = m-kt\) 表示走完 \(t\) 轮还需要走 \(w\) 步。
手动模拟一下，发现类似滑动窗口，每次暴力加入 \(w\) 步，计算答案，再删除当前点，把加入 \(w\) 步的点剩下的都加进去，时间复杂度为 \(O(n+k)\)。
注意 \(times=0\) 的情况和特判环大小 \(\le times\) 的情况。
(补）
Day 2
A 江桥的均衡区间
题目描述
解法
- Subtask 1 & Subtask 2
枚举 \(i\)，然后往后扩展，每次遇到一个数把他扔进去
- Subtask 3
枚举区间的起点终点，左右端点为 \(j,i(j<i)\)
\(p1_i-p1_{j-1}=p2_i-p2_{j-1}\)，移项，\(p1_i-p2_i=p1_{j-1}-p2_{j-1}\)。
