平邑集训(讲课)
Day 1
CF148E
题目描述
解法
容易发现当第 行要取出的数字个数固定时,所能得到的最大值与其他行无关。
设 表示第 行取 个数字所能得到的最大和。
容易得出:
那么求 数组的做法概括就为:枚举行() 枚举取出的数字个数() 枚举左边取出的数字()。时间复杂度 .
预处理完之后,考虑在每一组中有多少个数字,用分组背包来做。
CF95E
题目描述
解法
用并查集将每个联通快内的点数求出来,设为 。
将题意转化为:有若干个整数(之和为 ),从中最少取出所有个数字,使得相加之和为幸运数。
将整数的数值看成体积,同时要求最少取多少个数字恰好装满体积为 的背包。( 是任意一个幸运数)
用多重背包做,复杂度为 , 是物品种类, 是枚举的背包大小。
Day 2
(补)
Day 3
(补)
Day 4
(补)
Day 5
树的直径
- 定义:树上有边权,距离最远的两个点之间的距离(最长链)。
所以直径有两种情况:根节点到叶子节点和叶子结点到叶子结点。
求法:
- 树形 DP
设 号节点为根, 表示从节点 出发,走向以 为根的子树中能够到达的最远距离。
易得 。
发现对于第二种情况不好求,继续设 表示经过 节点向书中最长链的长度。
易得 。
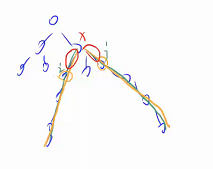
其中 就是图中的黄边。
但是复杂度会爆,因为求 数组的时间复杂度为 。
实际上可以在求 的时候顺便求一下 。
实现的时候可以用 记录答案,省下了数组 。
点击查看代码
bool vis[200001]; int cnt,head[200001]; struct node { int to,nxt,w; }e[200001]; void add(int u,int v,int w) { e[++cnt].to = v; e[cnt].w = w; e[cnt].nxt = head[u]; head[u] = cnt; } int ans,d[200001]; void dfs(int u) { vis[u] = 1; int i; for(i=head[u];i;i=e[i].nxt) { int v = e[i].to; if(vis[v]) continue; dfs(v); ans = max(ans,d[u]+d[v]+e[i].w); d[u] = max(d[u],d[v]+e[i].w); } return; }
- 贪心
也就是两遍 dfs。
1.从 号出发,找到距离 号节点最远的点 。
2.从 节点出发,找到距离 节点最远的点 。
所以从 到 的长度就是树的直径。
贪心是要证明的,所以证明一下 一定是直径的一个端点。
证明:
反证法,设 不是直径的一个端点,而 是距离 最远的点。
1.路径有交无重合。
假设有直径 。
因为
所以
所以 一定不会成为直径。
2.路径存有交有重合。
假设有直径 。
因为
所以
所以 一定不会成为直径。
3.完全无交。
假设有直径 。
所以 ,不然 就不是距离 最远的点了。
则
则
所以
所以 一定不会成为直径。
注意:贪心方法不能有负边权。
点击查看代码
int cnt,head[200001]; struct node { int to,nxt,w; }e[200001]; void add(int u,int v,int w) { e[++cnt].to = v; e[cnt].w = w; e[cnt].nxt = head[u]; head[u] = cnt; } int d[200001]; int p; void dfs(int u,int fa) { int i; for(i=head[u];i;i=e[i].nxt) { int v = e[i].to; if(v==fa) continue; d[v] = d[u]+1; if(d[v]>d[p]) p = v; dfs(v,u); } return; }
P3629 · 巡逻
题目描述
连接。
解法
当 时,一定是找个最长的链,连接端点,形成环。因此直接找直径即可。答案就是 。
当 时,第一条边就是连直径,第二条边需要分类讨论:
- 构成一个不与第一个环相交的环
如图: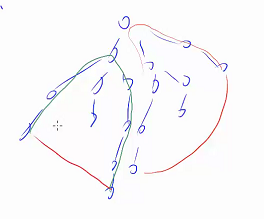
只要再贪心一次(把第一条直径上的边忽略)就可以了。
- 构成一个与第一个环相交的环
如图:
对于这两种情况,可以一起求。具体做法:
- 求出直径,那么就知道了 的值。
- 将直径上的边权从 赋值为 ,并再求出直径。
那就知道了 ,化简也就是 。
代码
树网的核
题目描述
给定一棵带边权无根树,在其直径上求出一段长度不超过 的路径 (核),使得离路径距离最远的点到路径的距离最短(题目中的定义是偏心距)。
解法
对于本题,中心点是唯一的,对于任意一条直径而言,求出的最小偏心距都是相等的。
- 解法一:枚举,时间复杂度 。
先求出直径的方案,枚举直径上距离不超过 的两个点作为核的端点,标记核上的点,从核上的每个点出发 dfs,求出核以外的每个节点到核的最短距离。
取最大值就是当前的偏心距。
不断枚举核,并求出当前路径为核的偏心距,取个最小值即可。
然后就过了原题。
- 解法二:优化为 。
树网的核长度不超过 ,当核的一个端点确定为 时,另一个端点 应该越远越好且不超过 。
维护一个 数组即可。
- 解法三:二分答案,优化为 。
剖析题目,要求最小的到核的最大距离,所以要最小化最大值,二分求解。
问题转化为,二分 ,然后判定是否存在一个核,使得其偏心距不超过 ?
从 出发,找到一个不超过 的最远点 ;再从 出发,找到一个不超过 的最远点 。如图: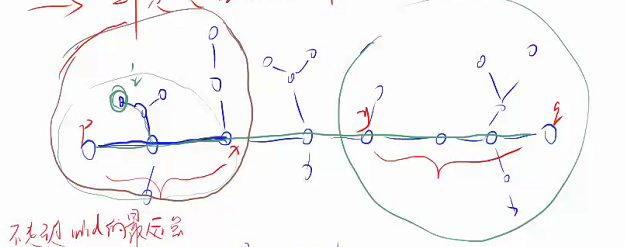
得到一个结论: 到 之间的分叉的子树,其最远点到 的距离不会超过到 的距离。而 到 同理。
现在就剩下中间那一坨点了。
需要判断两件事: 到 距离不超过 与 之间的子树上是否会超过 。
前者显然好判断,让 距离 最近即可;后者和解法二一样。
- 解法四:。
受解法三启发,我们表示一下偏心距离。如图:
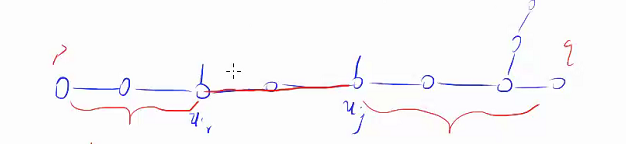
此时偏心距离为
设 表示从 出发,不经过直径上的点能够达到最远的点的距离。显然可以预处理,时间复杂度 。
若以 与 为核的端点,此时偏心距为 。
发现后半部分的 不能做到 。
对于这个 ,可以枚举 ,找到不超过 的最远的 。发现这是个在链上的滑动窗口,直接做就行。
代码
最近公共祖先
定义太简单,不说了。
- 向上标记法
1.让 一直向上走到根节点,并标记走过的点(也就是他的祖先);
2.让 向上走,遇到的第一个被标记过的点就是 和 的 LCA。
所以单次找 LCA 的时间复杂度就是 的。
- 树上倍增法
设 表示 的 辈祖先()。
例子: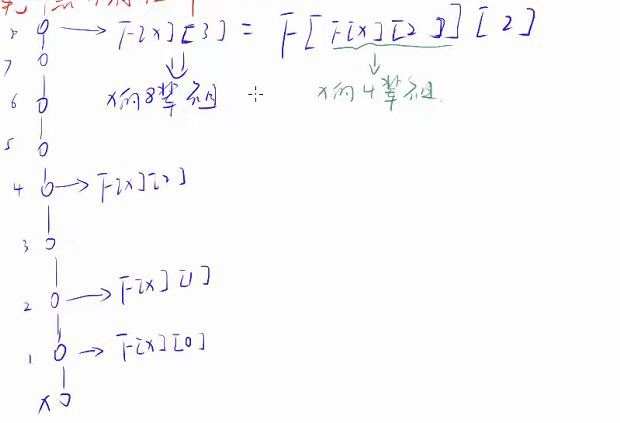
通过手玩样例,发现 ,而且如果祖先节点不存在,
具体原理也就是 \(2^k=2^{k-1]+2^{k-1}\),先走 步再走 步。
预处理 数组时间复杂度是 。
接下来就是正式求解了。
设 表示 的深度,且令 。
1.先把 调整到与 相同的深度,也就是 向上走 步。跳完后,若深度已经小于 ,选择用更小的步长走;若此时 (走到了同一层),则 就是 LCA。
2.尝试将 同同时向上走,步长依次为 步。若 ,则 。
3. 就差一步碰面,。
时间复杂度 。
点击查看代码
#include<bits/stdc++.h> using namespace std; const int N = 500000+114; struct edge { int to,w,nxt; }e[N*2]; int cnt,head[N]; int n,m,s; void add(int u,int v) { ++cnt; e[cnt].to = v; // e[cnt].w = w; e[cnt].nxt = head[u]; head[u] = cnt; } int lg[N],f[N][30],d[N]; void dfs(int u,int fa) { f[u][0] = fa; d[u] = d[fa]+1; int i; for(i=1;i<=lg[d[u]];i++) f[u][i] = f[f[u][i-1]][i-1]; for(i=head[u];i;i=e[i].nxt) if(e[i].to!=fa) dfs(e[i].to,u); return; } int lca(int x,int y) { if(d[x]<d[y]) swap(x,y); while(d[x]>d[y]) x = f[x][lg[d[x]-d[y]]-1]; if(x==y) return x; int i; for(i=lg[d[x]]-1;i>=0;i--) if(f[x][i]!=f[y][i]) x = f[x][i],y = f[y][i]; return f[x][0]; } int main() { cin>>n>>m>>s; int i,j; for(i=1;i<n;i++) { int u,v; cin>>u>>v; add(u,v); add(v,u); } for(i=1;i<=n;i++) lg[i] = lg[i-1]+(1<<lg[i-1]==i); dfs(s,0); while(m--) { int x,y; cin>>x>>y; cout<<lca(x,y)<<endl; } return 0; }
- 离线做法
dfs 一颗树的过程中,将节点分成三类:
1.已经访问过并且回溯了的点,标记为 。
2.已经访问,但没有回溯的点,标记为 。
3.尚未访问的点,不标记。
发现了一些性质:对于正在访问的点 ,从根到 的路径上标记都为 ,任意一个点 ,若标记为 ,则 一定是 向上走到根的路径中,第一个标记为 的点。
当一个点刚刚获得了 号标记,其父亲标记为 ,此时将其合并到父节点的集合。
当即将回溯到 时,扫描与 相关的所有询问( 标记为 ),可以回答所有标记为 的 的 。
P1967
题目描述
解法
加边方式类似最大生成树。
设 表示 的 辈祖先, 表示 的 辈祖先之间最小的边。
所以 。
(补)
树上差分
- 点差分
他能解决的问题:给定若干个 ,表示从 点走到 点。问每个点被经过的次数?
如果在序列上,直接差分再前缀和即可。树上也是如此。
例子: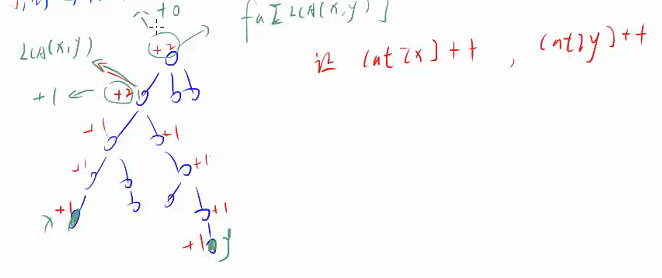
将 到根节点每个点 ,将 到根节点每个点 ,再减去 和 到根节点的距离即可。
也就是 cnt[x]++,cnt[y]++,cnt[lca(x,y)]--,cnt[fa[lca(x,y)]]--。
- 边差分
例子: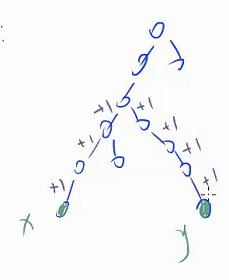
发现边权不好做,考虑下放在点权上。
转化为: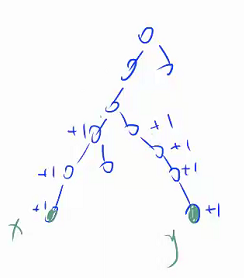
继续考虑差分,也就是 cnt[x]++,cnt[y]++,cnt[lca(x,y)] -= 2。
P3128
题目描述
解法
点差分板子。
代码
点击查看代码
#include<bits/stdc++.h> using namespace std; const int N = 500000+114; struct edge { int to,w,nxt; }e[N*2]; int cntt,head[N]; int n,m,s; void add(int u,int v) { ++cntt; e[cntt].to = v; // e[cnt].w = w; e[cntt].nxt = head[u]; head[u] = cntt; } int lg[N],f[N][30],d[N]; void dfs(int u,int fa) { f[u][0] = fa; d[u] = d[fa]+1; int i; for(i=1;i<=lg[d[u]];i++) f[u][i] = f[f[u][i-1]][i-1]; for(i=head[u];i;i=e[i].nxt) if(e[i].to!=fa) dfs(e[i].to,u); return; } int lca(int x,int y) { if(d[x]<d[y]) swap(x,y); while(d[x]>d[y]) x = f[x][lg[d[x]-d[y]]-1]; if(x==y) return x; int i; for(i=lg[d[x]]-1;i>=0;i--) if(f[x][i]!=f[y][i]) x = f[x][i],y = f[y][i]; return f[x][0]; } int cnt[200001]; int ma = INT_MIN; void get(int u,int fa) { int i; for(i=head[u];i;i=e[i].nxt) { int v = e[i].to; if(v==fa) continue; get(v,u); cnt[u] += cnt[v]; } ma = max(ma,cnt[u]); } int main() { cin>>n>>m; s = 1; int i; for(i=1;i<n;i++) { int u,v; cin>>u>>v; add(u,v); add(v,u); } for(i=1;i<=n;i++) lg[i] = lg[i-1]+(1<<lg[i-1]==i); dfs(1,0); while(m--) { int x,y; cin>>x>>y; int l = lca(x,y); cnt[x]++,cnt[y]++,cnt[l]--,cnt[f[l][0]]--; } get(1,0); cout<<ma<<endl; return 0; }
P3258
AcWing 354
题目描述
解法
对于非树边 而言,树上肯定有一个包含 的环。
第一次切环上的树边,第二次一定切 。
将 所在环上的所有树边的权值都加 。
如果是树边:
- 边权值为 ,显然第二刀随便砍,。
- 边权值为 ,只在一个环上,砍完以后只能砍非树边,所以 。
- 边权值 ,则起码需要 刀( 刀非树边+当前边),所以 不变。
代码
Day 6
DFS 序
- 时间戳
先了解什么时时间戳:在树的深度优先遍历中,以每个节点第一次被访问的顺序,以此给予这 个节点 到 的整数标记,该标记被称为时间戳。
给个例子: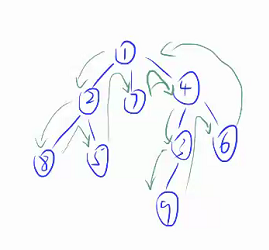

- 树的 DFS 序
在树的深度优先遍历中,对于每个节点进入递归后以及即将回溯各记录一次该点的编号,最后产生的长度为 到 的序列就被称为树的 DFS 序。
所以上面那棵树的 DFS 序就是 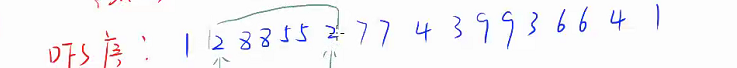
发现了一些性质:
1.每个节点在序列中恰好出现两次。
2.设 和 分别表示 出现两次的位置,那么区间 对应的就是在树上以 为根的子树。
LOJ 144 · DFS 序 1
题目描述
1.树上 节点的权值 。
2.询问 子树的权值和。
解法
代码
LOJ 145 · DFS 序 2
题目描述
1.节点 的子树上所有权值 。
2.询问 子树的权值和。
解法
求出 DFS 序,相当于在 DFS 序上进行区间加和区间查询。
用树状数组或者带标记的线段树。
先来看看树状数组怎么区间加区间查询。在 数组中, 加上 。
设 为差分数组,所以 ,。
操作结束后, 增加的值也就是 。
的前缀和 也就是 。
的前缀和增加量也就是 。
发现这个东西不好维护,先手玩一下: 被加了 , 被加了 , 被加了 , 被加了 。
所以刚刚那个式子可以表示为 。
发现最后要维护的就是上面那个式子的两个 。
开两个树状数组 。
- 对于区间加 :
1.在 中 add(l,b)。
2.在 中 add(r+1,-d)。
现在知道了前半部分的 的值。
3.在 中,add(l,l*d)。
4.在 中,add(r+1,-(r+1)*d)。
现在知道了后半部分的 的值。
- 对于区间求和 :
[sum[r]+(r+1)*ask(T1,r)-ask(T2,r)]-[sum[l-1]+l*ask(T1,l-1)-ask(T2,l-1)]。
代码
LOJ 146 · DFS 序 3,树上差分 1
题目描述
1.路径权值加。
2.单点查询。
3.子树权值求和。
解法
对于操作 可以直接树上差分,随着操作 就变成了子树查询。
问题是如何解决操作 。
设差分后, 节点的差分值是 。若 在以 为根的子树中,考虑 对于 这个子树权值和的增加量贡献。
得出:
于是 的子树增加量之和就是:
代码
LOJ 147 · DFS 序 4
题目描述
1.单点加。
2.子树权值加。
3.查询路径权值和。
也就是和上一题的查询/修改反着来。
解法
我们已经知道 到 的权值和了,所以考虑维护每个点到根的路径权值和。
对于操作 :节点 增加 ,相当于以 为根的子树中每个点到根的路径权值和都增加了 。
对于操作 :考虑 子树中的点 , 的变化。
代码
Day 7
树上 DP
分两种情况:从根到叶子( 是由父亲决定),从叶子到根( 是由子树决定)。
区间 DP
步骤是:拆分区间和合并区间。
背包 DP
Day 8
(补)
Day 9
(补)
Day 10
(补)
Day 11
(补)
Day 12
(补)
Day 13
(补)
Day 14
(补)
Day 15
(补)





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步