日照2024高算（讲课）

Day 1 · 数论

基本符号

• \(a\mid b\) 表示 \(b\) 是 \(a\) 的倍数；\(a\nmid b\) 表示 \(b\) 不是 \(a\) 的倍数。
• \(a \perp b\) 表示 \(a\) 与 \(b\) 互质。

数论入门

\(\gcd\) 的一些性质（欧几里得算法）

• \(\gcd(kn,km)=k\cdot \gcd(n,m)\)，\(lcm(kn,km)=k\cdot lcm(n,m)\)。

• 若 \(a\perp b\)，则 \(\gcd(a^m-b^m,a^n-b^n)=a^{\gcd(n,m)}-b^{\gcd(a,b)}\)。

• 若 \(n^a\equiv 1(mod m)\) 且 \(n^b\equiv1(mod m)\)，则 \(n^{\gcd(a,b)} \equiv 1(mod m)\)。

基于值域预处理的快速 \(\gcd\)

设 \(m=\sqrt n\)，用 \(O(n)\) 求出每个小于等于 \(m\) 的数对的 \(\gcd\)，假设要求 \(\gcd(x,y)\)，设 \(x=abc\)，则：

\[\gcd(x,y)=\gcd(a,y)\times\gcd(b,\dfrac{y}{\gcd(amy)})\times\gcd(c,\dfrac{y}{\gcd(ab,y)}) \]

ola回路（不重不漏） 哈密顿（点1，边无数）

（补）

Day 2 · 可持久化数据结构

（补）

Day 3 · 树形 DP+状压 DP

（补）

Day 4 · 动态规划及优化

单调队列优化 DP

Problem 1 Watching Fireworks is Fun

一个城镇有 \(n\) 个区域，从左到右编号为 \(1\sim n\)，个区域之间距离 \(1\) 个单位距离。

有 \(m\) 个烟火要放，给定放的地点 \(a_i\)，时间 \(t_i\)，如果你当时在区域 \(x\)，那么你可以获得 \(b_i - \vert a_i - x\vert\) 的开心值。

你每个单位时间可以移动不超过 \(d\) 个单位距离。

你的初始位置是任意的（初始时刻为 \(1\)），求你通过移动能获取到的最大的开心值。

（补）

斜率优化 DP

凸包

概念

可以想象成在一个无穷大的桌面上，有若干钉子，用一个长度极长且弹性极好的皮筋撑起来，包着最外面的钉子形成的图形就叫做凸包。

比如这个就是一个可爱的凸包：

解法 · Graham 扫描法

• 时间复杂度：\(O(nlogn)\)。

• 思路：先找到凸包上的一个点，然后从那个点开始按逆时针方向逐个找凸包上的点，实际上就是进行极角排序，然后对其查询使用。

• 步骤

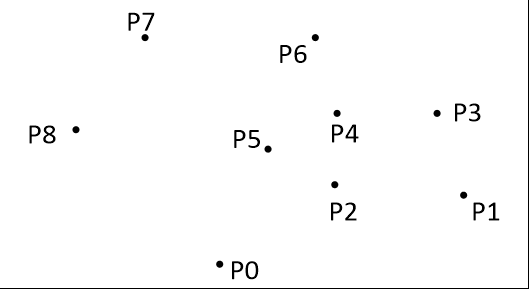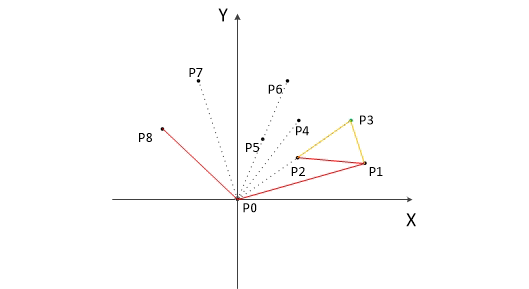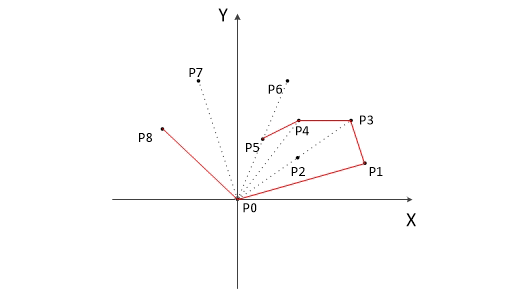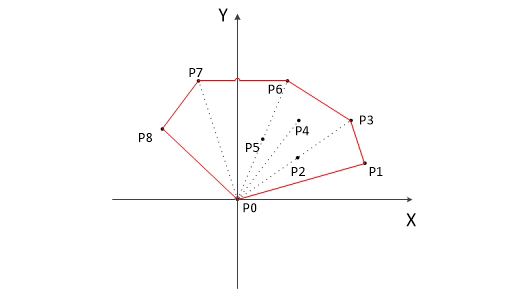
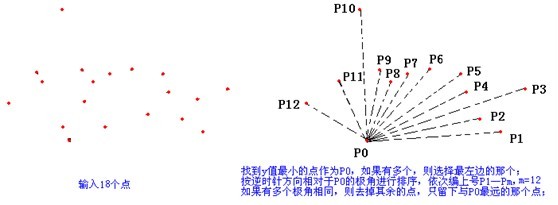
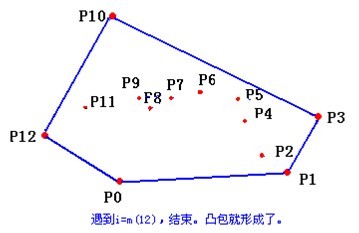
1. 把所有点放在二维坐标系中，则纵坐标最小的点一定是凸包上的点，如图中的 \(P_0\)。
2. 把所有点的坐标平移一下，使 \(P_0\) 作为原点，如上图。
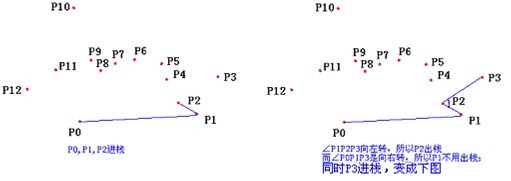
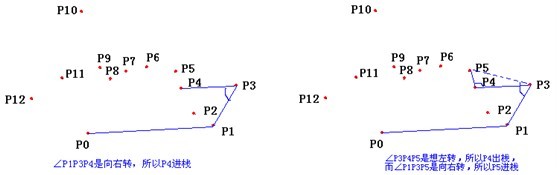
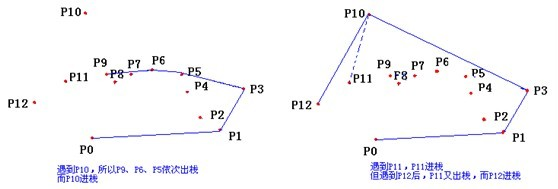
3. 计算各个点相对于 \(P_0\) 的幅角 \(\alpha\) ，按从小到大的顺序对各个点排序。当 \(\alpha\) 相同时，距离 \(P_0\) 比较近的排在前面。例如上图得到的结果为 \(P_1\)，\(P_2\)，\(P_3\)，\(P_4\)，\(P_5\)，\(P_6\)，\(P_7\)，\(P_8\)。我们由几何知识可以知道，结果中第一个点 \(P_1\) 和最后一个点 \(P_8\) 一定是凸包上的点。 （以上是准备步骤，以下开始求凸包）现在，我们已经知道了凸包上的第一个点 \(P_0\) 和第二个点 \(P_1\)，我们把它们放在栈里面。现在从步骤 \(3\) 求得的那个结果里，把 \(P_1\) 后面的那个点拿出来做当前点，即 \(P_2\) 。接下来开始找第三个点：
4. 连接 \(P_0\) 和栈顶的那个点，得到直线 \(L\) 。看当前点是在直线 \(L\) 的右边还是左边。如果在直线的右边就执行步骤 \(5\)；如果在直线上，或者在直线的左边就执行步骤 \(6\)。
5. 如果在右边，则栈顶的那个元素不是凸包上的点，把栈顶元素出栈。执行步骤 \(4\)。
6. 当前点是凸包上的点，把它压入栈，执行步骤 \(7\)。
7. 检查当前的点 \(P_2\) 是不是步骤3那个结果的最后一个元素。是最后一个元素的话就结束。如果不是的话就把 \(P_2\) 后面那个点做当前点，返回步骤 \(4\)。

最后，栈中的元素就是凸包上的点了。
以下为用 Graham 扫描法动态求解的过程：

下面静态求解过程：

• 代码

点击查看代码

#include <bits/stdc++.h>
using namespace std;
const int N = 1e6;
struct node
{
	double x, y;
} point[N];
int n, top = 2, st[N]; //top->栈顶，st->记录凸包上点的栈。
double ans, data_x, data_y;
inline double power(double x)
{
	return x * x;
}
inline double dis(int a, int b)
{
	return sqrt(power(point[a].x - point[b].x) + power(point[a].y - point[b].y));   //两点间距离。
}
inline bool judge(int a, int b, int c)
{
	return (point[a].y - point[b].y) * (point[b].x - point[c].x) > (point[a].x - point[b].x) * (point[b].y - point[c].y); //算斜率，乘在一起避免掉精。
}
inline bool cmp(node a, node b)
{
	return (a.y == b.y) ? (a.x < b.x) : (a.y < b.y);   //纵坐标小的在前，若相等，就取横坐标小的。
}
int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
	{
		scanf("%lf%lf", &point[i].x, &point[i].y);
	}
	sort(point + 1, point + n + 1, cmp);
	st[1] = 1, st[2] = 2; //前两点已经确定，入栈。
	for (int i = 3; i <= n; i++) //枚举其他的节点从3开始。
	{
		while (top > 1 && !judge(i, st[top], st[top - 1]))top--; //后者斜率（极角）小。
		st[++top] = i; //重新入栈。
	}
	for (int i = 1; i <= top - 1; i++)ans += dis(st[i], st[i + 1]);
	top = 2;
	memset(st, 0, sizeof(st)); //最好memset一下，有可能出问题。
	st[1] = 1, st[2] = 2;
	for (int i = 3; i <= n; i++)
	{
		while (top > 1 && judge(i, st[top], st[top - 1]))top--; //把！去掉就可以了。
		st[++top] = i;
	}
	for (int i = 1; i <= top - 1; i++)ans += dis(st[i], st[i + 1]); //后一边基本一样。
	printf("%.2lf", ans);
	return 0;
}

解法 · Andrew 算法

• 时间复杂度 \(O(nlogn)\)，但比 Graham 扫描法略快。

• 步骤：直接以横坐标为第一关键词、纵坐标为第二关键词排序（这样将顶点依次相连（不连首尾），也能保证不交叉）。先顺序枚举求上凸包，再逆序枚举求下凸包。用栈（手写栈可以直接访问下标）维护当前在凸包上的点，只要新点处在由栈顶两点构成的有向直线的右侧或共线，就弹出旧点。不能弹出时，新点入栈。正序和逆序都是一样的维护方式。

• 代码

点击查看代码

#include <bits/stdc++.h>
using namespace std;
#define N 200010
struct node
{
	double x, y;
} p[N], s[N];
int n, top;

double x(node a, node b, node c) //计算叉积
{
	return (b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x);
}
double dis(node a, node b) //距离
{
	return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
}
bool cmp(node a, node b)  //比较
{
	return a.x != b.x ? a.x < b.x : a.y < b.y;
}
double Andrew()
{
	sort(p + 1, p + n + 1, cmp); //排序
	for (int i = 1; i <= n; i++) //下凸包
	{
		while (top > 1 && x(s[top - 1], s[top], p[i]) <= 0)top--;
		s[++top] = p[i];
	}
	int t = top;
	for (int i = n - 1; i >= 1; i--) //上凸包
	{
		while (top > t && x(s[top - 1], s[top], p[i]) <= 0)top--;
		s[++top] = p[i];
	}
	double res = 0; //周长,视情况而定
	for (int i = 1; i < top; i++) res += dis(s[i], s[i + 1]);
	return res;
}

int main()
{
	cin >> n;
	int i;
	for (i = 1; i <= n; i++)
		cin >> p[i].x >> p[i].y;
	printf("%.2lf\n", Andrew());
	return 0;
}

Day 5 · Tarjan 和连通性问题

无向图的连通性

dfs 树

在 DFS 的过程中，所有经过的边组成了一棵树，这棵树称作 DFS 树。其中边分四类：

• 树边：指深度优先搜索树上的边。具体来说，如果上面的代码中这句话 if(!dfn[v]) dfs(v); 的 if 条件成立，即v没有被访问过、接下来要从 \(v\) 开始搜，那么边 \(u\to v\) 就被称为树边。

• 后向边：是指将节点 \(u\) 连接到其在深度优先搜索树中的祖先节点 \(v\) 的边 \(u\to v\)。在上面的代码中，我们并不能根据条件判断一条边是否一定是后向边，不过我们知道一定有 dfn[v] != 0 && dfn[v] <= dfn[u]。即 \(v\) 被访问过，且 \(v\) 比
  \(u\) 先被访问。自环（\(u\to u\)）也被认为是后向边（所以是小于等于）。

• 前向边：是指将节点 \(u\) 连接到其在深度优先搜索树中的后代节点 \(v\) 的边 \(u\to v\)。在上面的代码中，我们也不能根据条件判断一条边是否一定是前向边，不过我们知道一定有 dfn[v] != 0 && dfn[v] > dfn[u]。即 \(v\) 被访问过，且 \(v\) 比 \(u\) 后被访问。

举个例子：

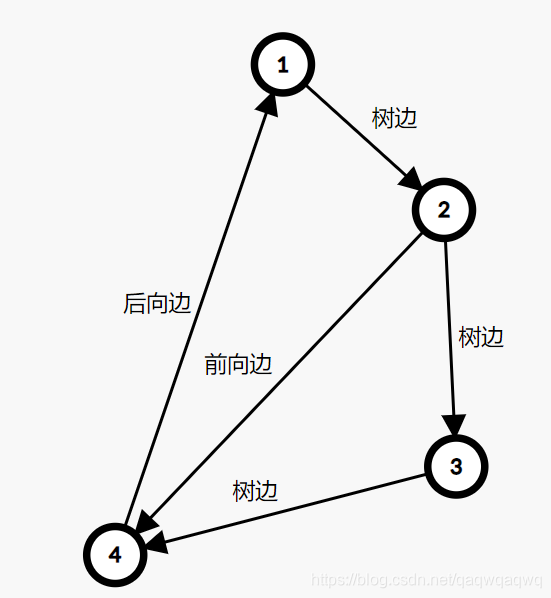
这张图中的搜索顺序为 \(1\to 2\to 3\to 4\)。节点 \(1、2、3、4\) 的时间戳（dfn）分别为 \(1、2、3、4\)。在考察边 \(2\to 4\) 的时候，由于 \(dfn_4>dfn_2\)，所以 \(2\to 4\)是前向边。又 \(dfn_1<dfn_4\)，故 \(4\to 1\) 是后向边。

• 横叉边。所有其他边都称为横叉边。换句话说，就是一个点不是另一个的点的祖先。这两个点可以在同一棵深度优先搜索树上，也可以在两棵不同的深度优先搜索树上。（一张图可以包含很多个深度优先搜索树。）

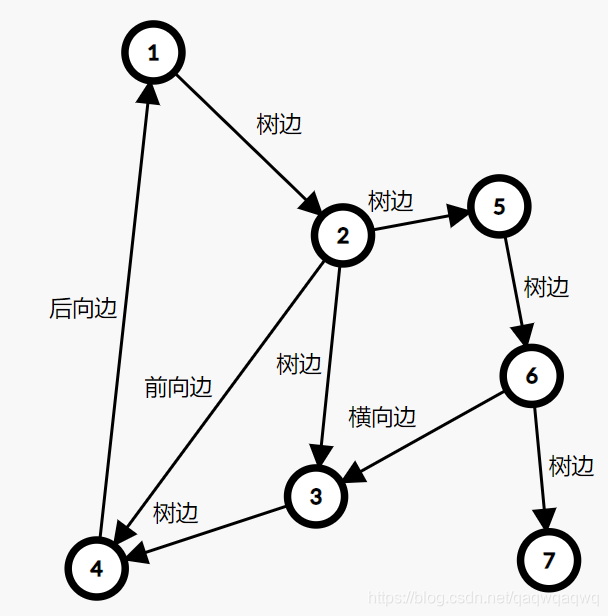
其中 \(6\to 3\) 是横向边（属于在同一棵树上的），因为 \(2\to 3\to 4\) 和 \(2\to 5\to 6\to 7\) 分别是树上的两条链，\(6\) 和 \(3\) 互相不是对方的祖先。

对于横叉边，有如下性质：

横向边 \(u\to v\) 满足 \(dfn_u>dfn_v\)。
证明：根据深度优先搜索的策略，访问到结点 \(u\) 之后，接下来会访问它所有邻接的未被访问的结点， \(u\) 到所有这些结点的边都是树边。因为此处 \(u\to v\) 不是树边，而是横向边，所以在访问 \(u\) 时 \(v\) 一定已被访问过。根据 \(dfn\) 随访问顺序严格单调递增，显然有 \(dfn_u>dfn_v\)。

再来一个实现过程的动画：

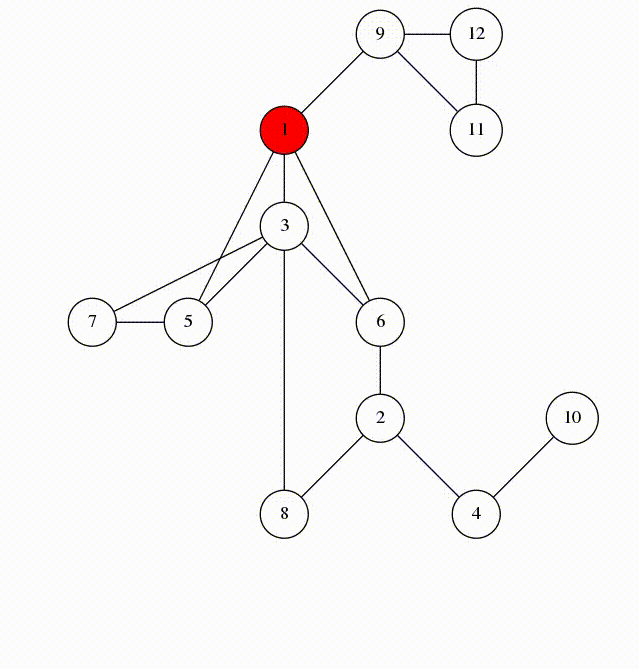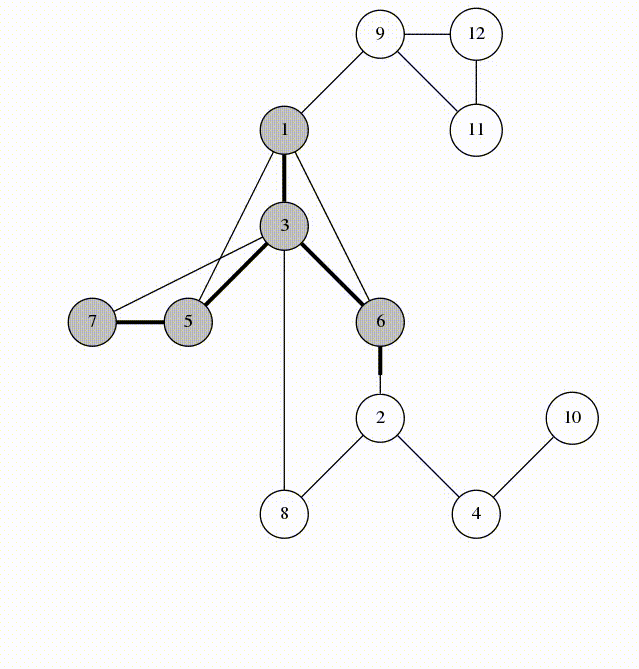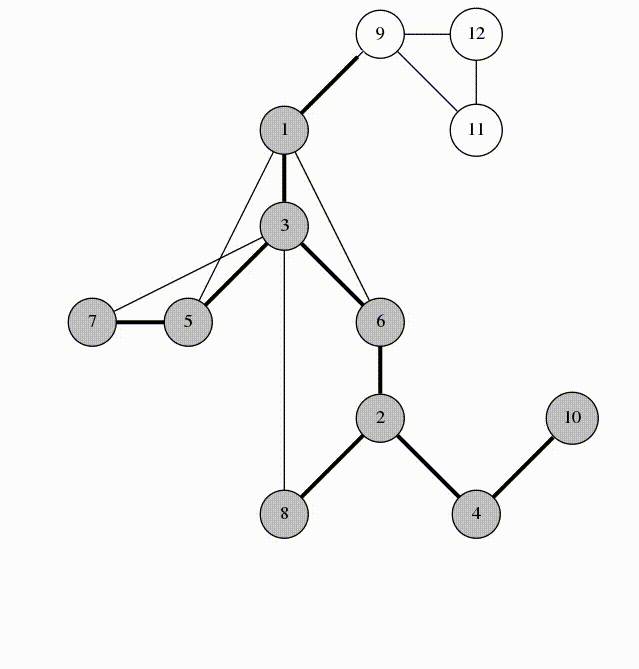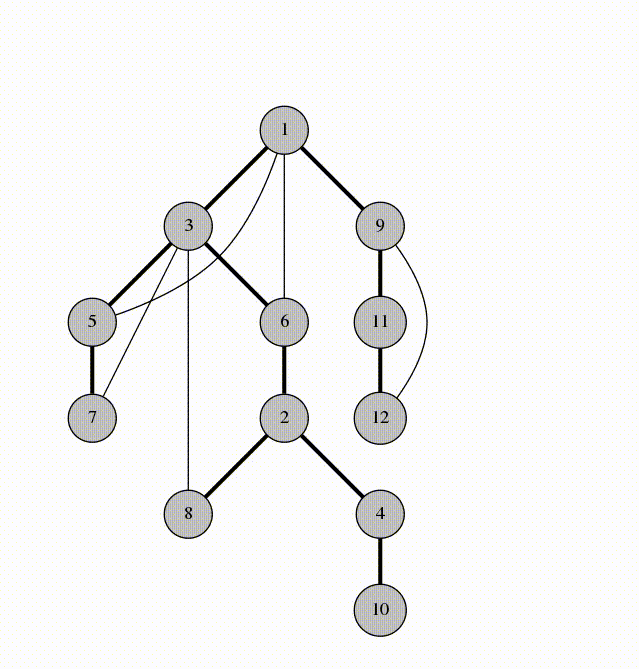
割点

一个点 \(u\) 是割点，那么必定存在一个儿子，删去 \(u\) 后和他的父亲不连通。如果不存在，和 \(u\) 相连的所有点依然连通，那么连通性不变，不是割点。

特别的，对于根节点，如果他有至少 2 个儿子，那么他就是割点。

• Tarjan 求割点

定义 \(dfn_u\) 表示点 \(u\) 的 dfs 序，\(low_u\) 表示 \(u\) 只通过自己和儿子，走到的所有点中的最小 dfn 序（从 \(u\) 出发，可以可以经过任意多条树边，最多经过一条非树边，到达的最小的 dfn）。

给一个图好理解：

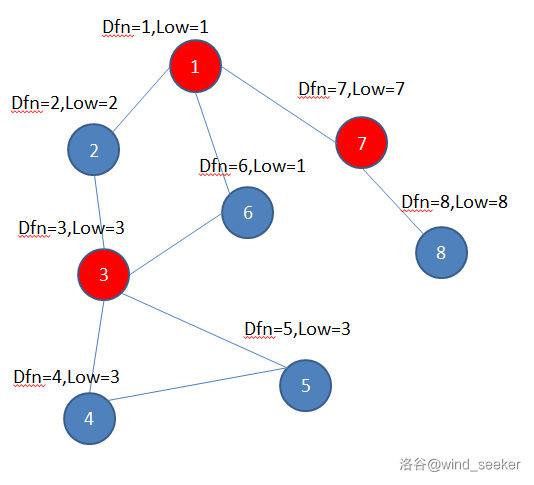
那么这两个数组怎么算？首先，第一次搜到 \(u\) 时，可以直接知道 \(dfn_u\)，

（补）

Day 6 · 字符串

最小表示

• 描述

最小表示法是求与某个字符串循环同构的所有字符串中，字典序最小的串是哪个。例如一个字符串 tzfakioi，它长为 \(8\)，也就是说最多有八种循环同构的方法。tzfakioi、zfakioit、fakioitz \(\cdots\) ，这几个串在原串上的开始位置分别是 \(0,1,2,3,4,5,6,7\)。默认从 \(0\) 开始比较方便，这一点之后也会再提到。

• 做法

暴力方法很简单，把所有的都列出来再排个序就行了，不再赘述。暴力的时间复杂度是很高的，然而我们可以做到 \(O(n)\) 求出字典序最小的串的开始位置。

设 \(i,j\) 是两个“怀疑是最小的位置”，比如说如果你比较到了 tzfakioi 的两个 i，你目前还不知道从哪个 i 开始的字符串是最小的。

设 \(k\) 表示从 \(i\) 往后数和从 \(j\) 往后数，有多少是相同的。开始时先设 \(i=0,j=1,k=0\)，每次都对 \(i+k,j+k\) 进行一次比较。

可是 \(i+k\) 有可能大于 \(n\)，如果复制一份，比较麻烦，而且前后两段是一样的，所以我们只要对 \(n\) 取模即可，也就是 \((i+k)\mod n\)。

既然出现了 \(\mod\)，那么下标从 \(0\) 就比较好，如果出现 \(1\)，那就要 \(+1,-1\)，非常麻烦。

比较完 \(i+k\) 和 \(j+k\)，如果两个字符相等，那么显然就 k++；如果不相等，那么哪边比较大，哪边就肯定不是最小的了，同时把 \(k\) 重置为 \(0\)；如果出现了 \(i,j\) 重合的情况，把 \(j\) 往后移动一位。

最后输出 \(i,j\) 较小的那个就好了。

（代码，补）

manacher

• 描述

在 \(O(n)\) 的时间复杂度求出以每个位置为回文中心的最长回文半径。

• 做法

前置知识：回文中心。

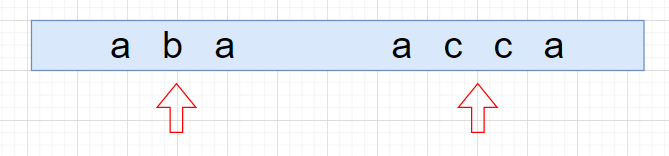
此时发现如果回文字符串长度为偶数时，回文中心不能恰好落到某个数组下标处，为了统一操作，在每个字符中间添加一个特殊字符，如：

前置知识：最长回文子串。

以 \(i\) 下标为回文中心的回文半径，可以理解为人的臂长。例如上图红色的 \(4\)。

那么我们可以枚举每个

附 · 交互题