Booth算法

Booth算法

算法描述（载自维基百科）

---

对于N位乘数Y，布斯算法检查其2的补码形式的最后一位和一个隐含的低位，命名为y-1，初始值为0。对于yi, i = 0, 1, ..., N - 1，考察yi和yi - 1。当这两位相同时，存放积的累加器P的值保持不变。当yi = 0且yi - 1 = 1时，被乘数乘以2i加到P中。当yi = 1且yi - 1 = 0时，从P中减去被乘数乘以2i的值。算法结束后，P中的数即为乘法结果。

该算法对被乘数和积这两个数的表达方式并没有作规定。一般地，和乘数一样，可以采用2的补码方式表达。也可以采用其他计数形式，只要支持加减法就行。这个算法从乘数的最低位执行到最高位，从i = 0开始，接下来和2i的乘法被累加器P的算术右移所取代。较低位可以被移出，加减法可以只在P的前N位上进行。

算法原理

---

请参考维基百科 布斯乘法算法

Verilog代码

---

Design code

---

module booth 
            #(
                parameter  MUT_WIDTH = 6,
                parameter  CNT_WIDTH = MUT_WIDTH/2
             )
            (
            output  reg  [MUT_WIDTH - 1:0]   A,
            output  reg  [MUT_WIDTH - 1:0]   Q,
            output  reg                      done,

            input                            clk,
            input                            rst_n,
            input        [MUT_WIDTH:0]       Qi,
            input        [MUT_WIDTH:0]       M,
            input                            start
            );

reg                      Q1;
reg  [CNT_WIDTH - 1:0]   cnt;
reg  [CNT_WIDTH - 1:0]   cnt_next;
reg  [MUT_WIDTH - 1:0]   Atemp;

always@(posedge clk,negedge rst_n)
begin
    if(!rst_n)
    begin
        A    <= 0;
        Q    <= 0;
        Q1   <= 1'b0;
        done <= 1'b0;
    end
    else if(start)
    begin
        A    <= 6'b0;
        Q    <= Qi;
        Q1   <= 1'b0;
        done <= 1'b0;
    end
    else if(cnt > 0)
        {A,Q,Q1} <= {Atemp[MUT_WIDTH - 1],Atemp,Q};
    else
        done <= 1'b1;
end

always@(*)
begin
    if(!start && cnt >0)
    begin
       case({Q[0],Q1})
           2'b10:Atemp = A - M;
           2'b01:Atemp = A + M;
           default: Atemp = A;
       endcase
    end
    else
        Atemp = 6'b0;
end

always@(posedge clk,negedge rst_n)
begin
    if(!rst_n)
        cnt <= 0;
    else if(start)
        cnt <= MUT_WIDTH;
    else
        cnt <= cnt_next;
end

always@(*)
begin
    if(start)
        cnt_next = cnt;
    else if(cnt > 0)
        cnt_next = cnt - 1'b1;
    else
        cnt_next = cnt;
end
endmodule

endmodule

testbench

---

module booth_tb;
    parameter n=12;

    wire   [n-1:0]   A;
    wire   [n-1:0]   Q;
    reg    [n-1:0]   Qi;
    reg    [n-1:0]   M;
    reg              start;
    wire             done;
    reg              clk;
    reg              rst_n;
    wire   [2*n-1:0] result;

booth #(.MUT_WIDTH(n),
        .CNT_WIDTH(n/2)
       )
       u_booth(
              .A(A),
              .Q(Q),
              .done(done),

              .clk(clk),
              .rst_n(rst_n),
              .Qi(Qi),
              .M(M),
              .start(start)
              );


    initial
    begin
        clk=1'b1;
        rst_n = 1'b0;
        #20 rst_n = 1'b1;

        M=12;
        Qi=-17;
        #1 start=1;
        #4 start=0;
        #40 start=1;

        M=5;
        Qi=-5;
        #20 start=0;
        #100 $finish;
    end

    always
        #1 clk=~clk;

    assign result={A,Q};

    initial begin
        $fsdbDumpfile("tb.fsdb");
        $fsdbDumpvars;
    end

endmodule

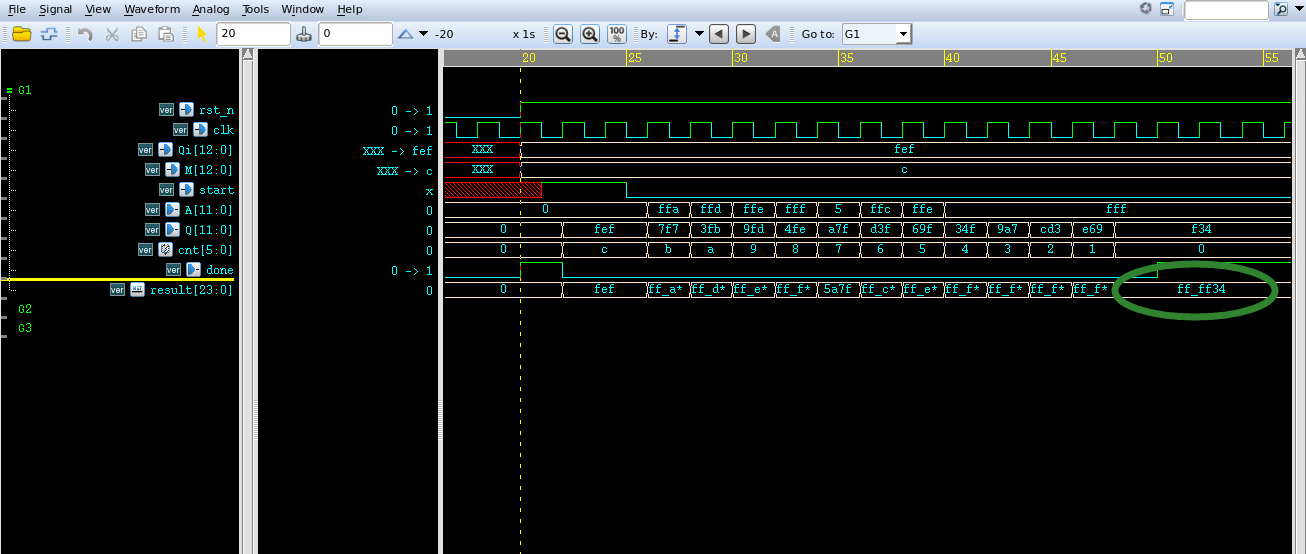
仿真结果

---

参考资料

---

[1].布斯乘法算法
[2].Booth算法的硬件实现
[3].Booth算法