CF1867E2 Salyg1n and Array (hard version)

写在前面

做 E1 的时候，直接想的正解，所以 E2 不需要改代码，E1 题解我也直接交的正解，详见我的题解。

在这里呢，主要是稍微证明一下询问次数不会超，如下：

可以发现，有余数的情况，只会增加两次询问，而后面的操作会增加 \(\frac n k\) 次情况，因为 \(k\le n\le k^2\)，所以询问最大次数是 \(k+2\)，也就是 \(52\) 次，所以不仅能过 E1，E2 也是随便过的。

题解

还是放一下题解，当然和 E1 没有什么区别。

思路

首先考虑，\(n\) 是 \(k\) 的倍数的情况，直接枚举询问所有每一段就好，然后输出每一段的异或和的异或和。

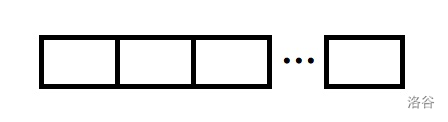
如上图，每次询问都没有重叠部分，颠转互不干扰。

那么，\(n\) 不是 \(k\) 的倍数的情况呢？

可以看到，与第一种情况的区别就是末尾多了一小截，那么我们需要考虑如何计算这一小截的异或和。

很容易想到，提前在前面计算这个长度的异或和，后续就可以和第一种情况一样了。

可以发现，解题的关键就是查询后会颠转这个特殊性质，见下图：

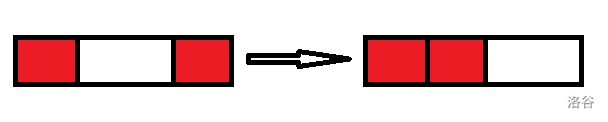
因为异或的性质，自己异或自己会变成 \(0\)，所以同一段的异或两次就会变成 \(0\)。使用这个性质可以发现，如果两个询问区间重叠，那么因为颠转，获得的异或和会转移到一起。

那么我们可以考虑先构造出前面一截是余数长度的区间的异或何，后续就是第一种情况了。

因为每次取得区间长度都是固定的，所以两段红色的区间长度也一定一样，因为两段长度和是余数，所以一段我们就取余数的一半。

因为 \(n\) 和 \(k\) 在题目中都给定了是正偶数，所以不用担心余数是奇数的情况。

AC code

#include<bits/stdc++.h>
using namespace std;
int T,n,k,sum,a;
int main()
{
	cin>>T;
	while(T--)
	{
		cin>>n>>k,sum=0;
		if(n%k)
		{
			cout<<"? 1"<<endl;
			cin>>a,sum^=a;
			cout<<"? "<<1+(n%k)/2<<endl;
			cin>>a,sum^=a;
		}
		for(int i=(n%k)+1;i<=n;i+=k) cout<<"? "<<i<<endl,cin>>a,sum^=a;
		cout<<"! "<<sum<<endl;
	}
	return 0;
}