P9554 「CROI · R1」浣熊的溪石
思路与分析
这道题乍一看还挺难的，但是如果把这个序列拆成两半就会容易一些。
首先，讨论一下序列长度 \(n\)，如果 \(n\) 为偶数，就可以对半分开；如果是 \(n\) 奇数，就把中间那位单独拿出来，然后再对半分开。
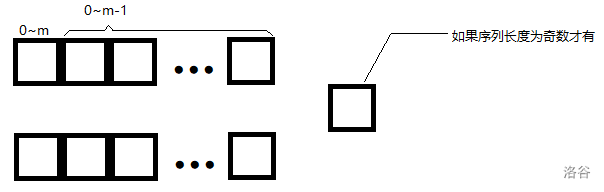
我们称上面一部分为 \(a\) 序列，下面一部分为 \(b\) 序列。
需要注意的是，这里 \(b\) 序列的方向与总序列和 \(a\) 序列有点不同，如下图：
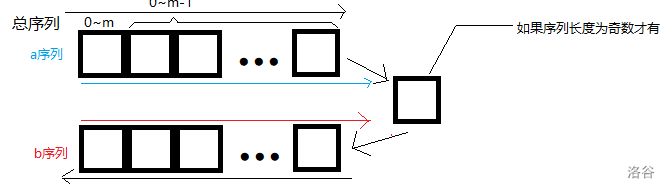
黑线的方向代表总序列的顺序，蓝线的方向代表 \(a\) 序列的顺序，红线的方向代表 \(b\) 序列的顺序。
我们可以发现如果 \(a\) 序列和 \(b\) 序列交换一下，总序列就相当于颠倒了一次，根据题意，这两个序列算相同的。
如果只关注 \(a\) 序列，不考虑其他的，总共有 \(M=(m+1)\times m^{\lfloor n/2\rfloor-1}\) 种可能。
我们来大概模拟一下过程：
- \(a\) 序列随机选一种，那么 \(b\) 序列共有 \(M\) 种取法。
- \(a\) 序列在剩下的情况中再随机选一种，那么 \(b\) 序列不能选择 \(a\) 序列上次选择的那个，否则就会和上一步的某个序列相同了（因为 \(a\) 的取法定然包含于第一步 \(b\) 的某个取值，如果 \(b\) 和第一步 \(a\) 一样，就等于总序列颠倒一次，算同种序列），所以共有 \(M-1\) 种取法。
\(\cdots\)
我们发现如果只考虑 \(a\) 序列和 \(b\) 序列的话，共有 \(\frac{M\times (M+1)}{2}\) 种情况，如果 \(n\) 为奇数，那就再乘上 \(m\) 就好了，因为单独的中间格子无论怎么取都不会有影响。
所以整个过程就会变得非常简单，先求出 \(M\) 然后再算一遍 \(\frac{M\times (M+1)}{2}\)，再判断个特殊情况。
优化还是懒？
只是，我们发现过程种有个除以 \(2\) 的过程，再取模的情况下，我们需要求逆元，但是我实在是太懒了，懒得写拓欧，所以我就想了个取巧的偷懒方法。
因为 \((m+1)\) 和 \(m\) 中必定有一个是偶数，所以我们先在取模前就除以个 \(2\)。也就是说求 \(M\) 时，我们先除以 \(2\) 得到 \(N=\frac{M}{2}=\frac{m\times (m+1)}{2} \times m^{\lfloor n/2\rfloor-2}\)。
然后再算 \(N\times (2\times N+1)\)。
这样就不需要拓展欧几里得求逆元了，当然，\(n\) 比较小的时候就需要特判了。
AC 代码
#include<bits/stdc++.h>
using namespace std;
const unsigned long long mod=998244353;//当时不知道为什么，复制模数的时候复制了两边，后面才发现，索性就全开unsigned long long了
unsigned long long T,n,m,a;
unsigned long long qsm(unsigned long long a,unsigned long long b)//快速幂
{
unsigned long long ans=1;
while(b)
{
if(b&1) ans=a*ans%mod;
a=a*a%mod,b>>=1;
}
return ans;
}
int main()
{
scanf("%llu",&T);
while(T--)
{
scanf("%llu%llu",&n,&m);
if(n==1) printf("%llu\n",(m+2)%mod);//特判，这个最简单了，我觉得不需要讲
else if(n==2) printf("%llu\n",(m+2)*(m+1)/2%mod);
else if(n==3) printf("%llu\n",(m+2)*(m+1)/2%mod*m);//把n比较小的特判了
else if(n%2==0) a=(m+1)*m/2%mod*qsm(m,n/2-2)%mod,a=(2*a%mod+1)*a%mod,printf("%llu\n",a%mod);//n为偶数的情况
else a=(m+1)*m/2%mod*qsm(m,n/2-2)%mod,a=(2*a%mod+1)*a%mod,printf("%llu\n",a*m%mod);//n为奇数的情况，要多乘以一个m
}
return 0;
}
P.S.偷懒是第一生产力（doge
