P1761 正方形
思路
第零步：规避精度问题
发现该题中正方形的放置在确定各正方形的大小后是固定的，而当正方形的大小同时变化相同倍数时，也可看做整个图像变化倍数，发现对答案没有影响，又发现遮挡和对角线有密切关系，而与边长无关系，再加上对角线等于 \(\sqrt{2}\) 倍边长，出现了精度问题，所以为了规避这一问题，我们可以把正方形整体放大 \(\sqrt 2\) 倍，即对角线看做边长长度的 \(2\) 倍。
同时，我们发现后续操作应该与对角线长度的 \(\frac 1 2\) 有关，所以我们放大 \(\sqrt 2\) 倍，而非缩小 \(\sqrt 2\) 倍，以避免出现小数，下文用 \(a_i\) 代表对角线长度。
第一步：确定正方形位置
因为要确定当前正方形的位置时，前一个正方形一定已经确定了位置，那么我们可以根据前面已确定的位置来确定下一个，为了方便储存，我们用正方形的中心位置来代表一个正方形的位置。
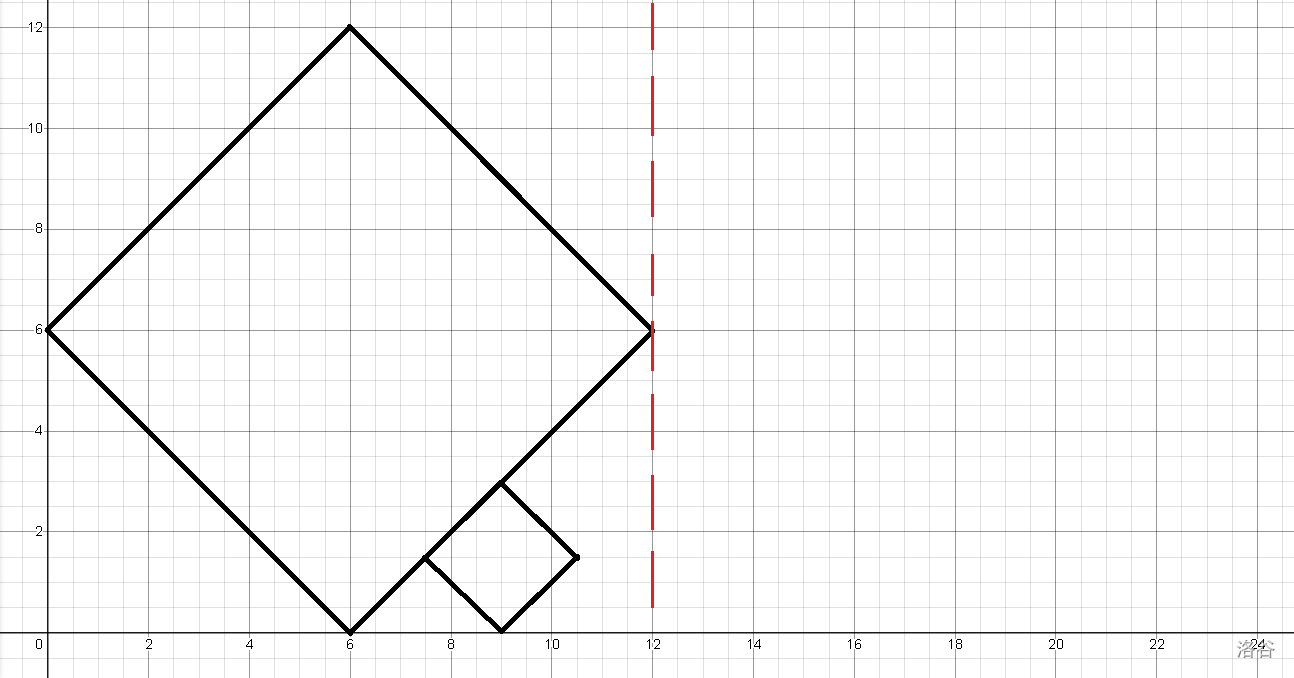
我们可以先手玩找找规律，如下图（红线代表正方形的中心水平距离）。
我们可以发现，中心水平距离就是两正方形中对角线长度较小者的对角线长度。
证明也挺好证的，先考虑新正方形较小的情况。
因为是 \(45°\) 放置的，所以可以得知图中红色线段和绿色线段都应该是 \(\frac 1 2\) 倍的对角线长度，而两者之和就是中心水平距离。
再考虑新正方形较大的情况，其实就是把两者反转一下，与上面一种情况一样。
但是需要注意的是，我们目前只考虑前面一个正方形对新正方形的影响，如果前面还有特别大的正方形呢？
所以我们需要考虑所有已放置的正方形，取所有算出来的中心的最大值。
for(int i=1;i<=n;++i)
for(int j=1;j<i;++j)
p[i]=max(p[i],p[j]+min(a[j],a[i]));
第三步：确定是否被覆盖
一个正方形什么时候被覆盖？
设第 \(i\) 个正方形左边的正方形最长的延伸长度为 \(l_i\)，右边的正方形最长的延伸长度为 \(r_i\)。
一共 \(3\) 种情况会导致这个正方形被覆盖。
- \(l_i\) 大于等于该正方形最右边的位置，即 \(l_i \geq p_i+\frac{a_i}{2}\)。
- \(r_i\) 小于等于该正方形最左边的位置，即 \(r_i \leq p_i-\frac{a_i}{2}\)。
- \(l_i\geq r_i\)。
但是需要注意的是，如果正方形的对角线长度小于该正方形，则不应该用来算 \(l_i,r_i\)。
因为所有的正方形的下面那个顶点都是放在 \(x\) 轴上的，所以对角线长度越大，那这个正方形的高度就越高，如果另一个正方形对角线长度小，那么就会在该正方形的下面，不会遮住该正方形。
如下图，左边的正方形不会对右边的正方形的 \(l_i\) 做出贡献。
另外，我们可以把三种情况合并在一起，只需要最后进行 \(l_i=max(l_i,p_i-\frac{a_i}{2}),r_i=min(r_i,p_i+\frac{a_i}{2})\)，就可以三种情况一起判断了。
for(int i=1;i<=n;++i)
{
for(int j=1;j<i;++j) if(a[j]>a[i]) r[i]=max(r[i],p[j]+a[j]/2);
r[i]=max(r[i],p[i]-a[i]/2);
}
for(int i=1;i<=n;++i)
{
for(int j=i+1;j<=n;++j) if(a[j]>a[i]) l[i]=min(l[i],p[j]-a[j]/2);
l[i]=min(l[i],p[i]+a[i]/2);
}
AC 代码
#include<bits/stdc++.h>
using namespace std;
int n,a[105],p[105],r[105],l[105];
int main()
{
while(~scanf("%d",&n)&&n)
{
memset(p,0,sizeof(p)),memset(l,0x3f,sizeof(l)),memset(r,0x8f,sizeof(r));
for(int i=1;i<=n;++i)
{
scanf("%d",&a[i]),a[i]*=2;
for(int j=1;j<i;++j) p[i]=max(p[i],p[j]+min(a[j],a[i]));
}
for(int i=1;i<=n;++i)
{
for(int j=1;j<i;++j) if(a[j]>a[i]) r[i]=max(r[i],p[j]+a[j]/2);
r[i]=max(r[i],p[i]-a[i]/2);
}
for(int i=1;i<=n;++i)
{
for(int j=i+1;j<=n;++j) if(a[j]>a[i]) l[i]=min(l[i],p[j]-a[j]/2);
l[i]=min(l[i],p[i]+a[i]/2);
}
for(int i=1;i<=n;++i) if(r[i]<l[i]) printf("%d ",i);
puts("");
}
return 0;
}
