圆方树学习笔记
前置芝士
边双连通与点双连通
oi-wiki 上是这样说的:
在一张连通的无向图中,对于两个点
和 ,如果无论删去哪条边(只能删去一条)都不能使它们不连通,我们就说 和 边双连通。
在这里我们需要得出一个非常重要的性质:边双连通具有传递性。通俗来说,就是当
再来,那么点双连通是什么?oi-wiki 上是这么说的:
在一张连通的无向图中,对于两个点
和 ,如果无论删去哪个点(只能删去一个,且不能删 和 自己)都不能使它们不连通,我们就说 和 点双连通。
好的。这里就容易有同学推出一个假结论:点双连通和边双连通一样具有传递性。
这显然是错误的,我们来一起举个例子。
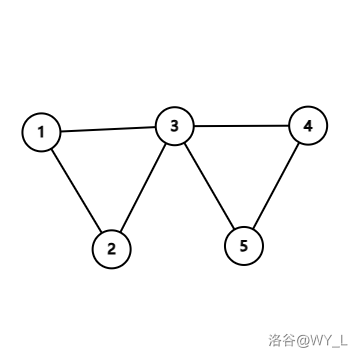
首先,我们来看边双连通:
再来看点双连通,同样的
这是一个非常重要的结论,下面的圆方树就很优雅的解决了这个问题。
圆方树
圆方树是一种将图变成树的方法,在求解某些类似于必经点的问题时非常好用,不失为一种极其优雅的方法。后面给出例题就能很明显的看出圆方树的优势了。
圆方树对于点双连通的解决方案,就是对于每一个已有的点双连通分量新建一个方点,将所有在这个点双连通分量里的点全部和这个方点连一条边。再把原来的边全部断掉,然后就形成了一棵美丽的树。
这里再来举个例子,这张图里展现了一个普通图变成圆方树的过程。
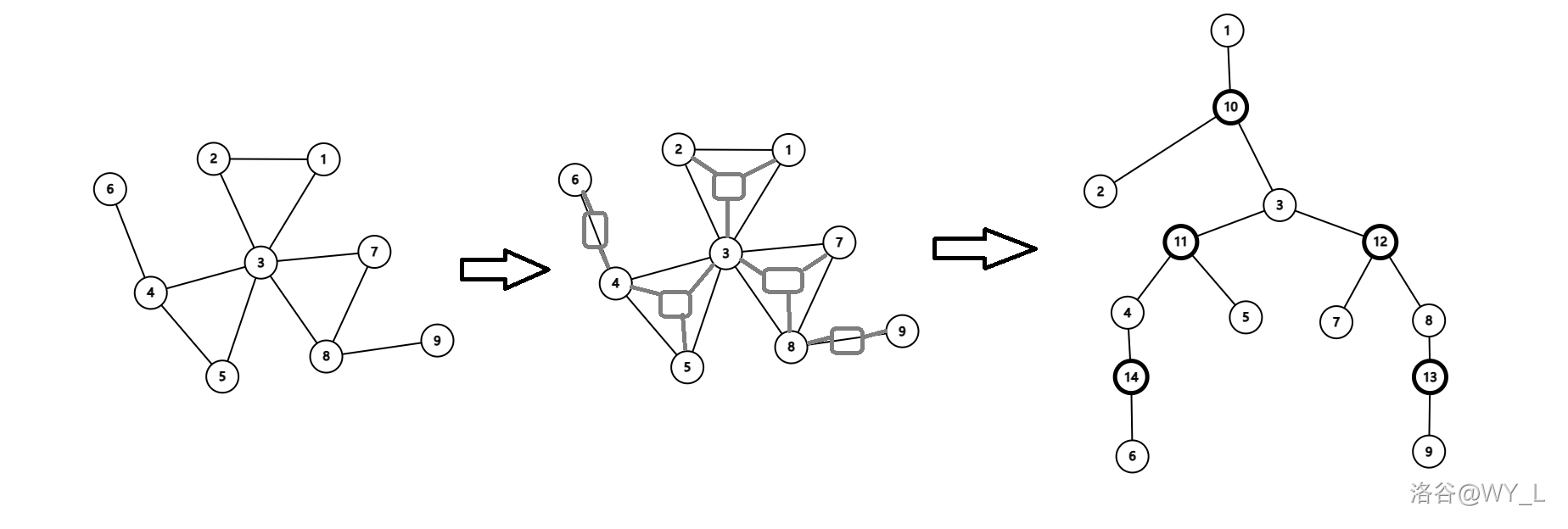
特别地,这里将 1 节点看作了根节点,这个无伤大雅。这里注意,我们将两个点间只有 1 条边的情况也视作点双连通,所以 8 节点和 9 节点也是点双连通的。
然后。我们考虑如何实现。我们可以沿用 tarjan 的思想。甚至是直接在 tarjan 求点双连通分量的基础上进行修改。
同样,我们定义如下两个数组:
与 tarjan 一样,我们再使用一个栈记录没有确定的点双节点。每次找到一个以
点击查看代码
vector<int> Tree[N];//圆方树存图
int low[N],dfn[N],Stack[N],top,cnt;
void Tarjan(int u){
dfn[u]=low[u]=++cnt;
Stack[++top]=u;
for(int i=head[u];i;i=Next[i]){
int v=to[i];
if(!dfn[v]){
Tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]==dfn[u]){
cnt++;
for(int x=0;x!=v;top--){
x=Stack[top];
Tree[cnt].push_back(x);
Tree[x].push_back(cnt);
}
Tree[cnt].push_back(u);
Tree[u].push_back(cnt);
}
}else if(v!=fa[u]){
low[u]=min(low[u],dfn[v]);
}
}
return;
}
然后,其实就没有然后了。这上面就是圆方树基本思想,我们来看例题吧qwq。
例题
[ABC318G] Typical Path Problem
题意
给定一个无向连通图,给出图上三个不同的顶点
思路
其实看到使用输出 Yes 和 No 而且不是多测,第一时间想到的就是不可以总司令(乐。
好了好了,不扯了。进入正题。首先,我们直接考虑将原图变成一个圆方树。然后,思考什么时候可以从
-
-
第一种情况显然是无解的。那第二种情况呢,这也很显然。这里先给出结论:
- 如果
这个应该是很好证明的。因为连接方点的圆点和方点的其他出边所连的原点在同一个点双连通分量里。那么一定有路径从
AC code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace WYL{
const int N=4e5+10;
int n,m,Low[N],dfn[N],top,father[N],Stack[N],nxt[N<<1],head[N<<1],to[N<<1],tot,a,b,c,times,cnt;
vector<int>Tree[N];
void add(int u,int v){
nxt[++tot]=head[u];
head[u]=tot;
to[tot]=v;
return;
}
void tarjan(int u){
Low[u]=dfn[u]=++times;
Stack[++top]=u;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(!dfn[v]){
tarjan(v);
Low[u]=min(Low[u],Low[v]);
if(Low[v]==dfn[u]){
++cnt;
int x;
// while(x!=v){
// x=Stack[--top];
// Tree[cnt].push_back(x);
// Tree[x].push_back(cnt);
// }
for(int x=0;x!=v;--top){
x=Stack[top];
Tree[cnt].push_back(x);
Tree[x].push_back(cnt);
}
Tree[cnt].push_back(u);
Tree[u].push_back(cnt);
}
}else{
Low[u]=min(Low[u],dfn[v]);
}
}
}
void dfs(int u,int fa){
father[u]=fa;
for(int i=0;i<Tree[u].size();i++){
int v=Tree[u][i];
if(v!=fa){
dfs(v,u);
}
}
return;
}
bool check(int u){
while(u!=c){
if(u>n){
for(int v:Tree[u]){
if(v==b){
return true;
}
}
}
u=father[u];
}
return false;
}
int main(){
cin>>n>>m>>a>>b>>c;
cnt=n;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
add(u,v);add(v,u);
}
for(int i=1;i<=n;i++){
if(!dfn[i]){
tarjan(i);
--top;
}
}
// for(int i=1;i<=n+cnt;i++){
// for(int j=0;j<Tree[i].size();j++){
// cout<<Tree[i][j]<<" ";
// }
// cout<<endl;
// }
// cout<<endl;
dfs(c,0);
if(check(a)){
cout<<"Yes"<<endl;
}else{
cout<<"No"<<endl;
}
return 0;
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
WYL::main();
return 0;
}
// 如果从 a 到 c 的路上有一方点可以直接到达 b,则输出Yes,否则输出No。
P4320 道路相遇
题意
还是给定一个无向连通图,给出一些起点和终点,对于每一组询问,给出每种可能的路径都要经过的一个点。
思路
第一眼其实挺迷茫的,我们尝试画图解决。当然先把圆方树建了。我把样例拿下来画了一下。
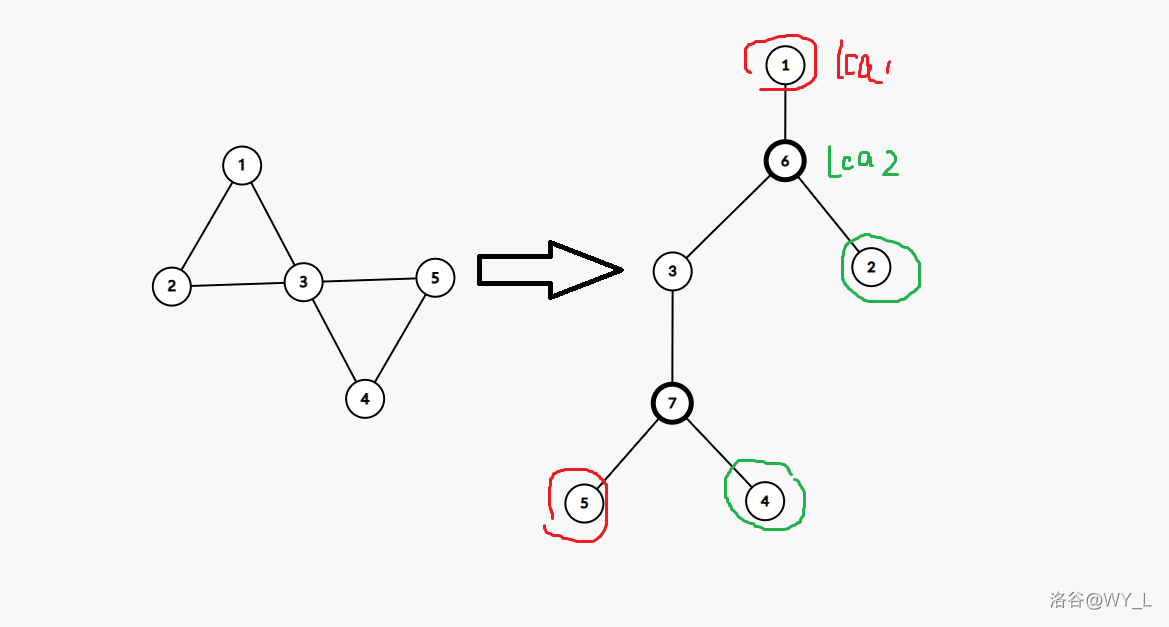
锐评:这个图长得也是十分清纯可爱。
首先一个很简单的转换,题目其实就是再求原图的割点。那么又因为起点和终点一定都是圆点。而且圆点一定连接着方点。所以一个美丽的结论就出来了:答案就是起点与终点之间的路径长度除以 2 再加 1。
实现上就直接 LCA 求最近公共祖先,然后求路径长度,就搞定啦(喜。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
namespace WYL{
const int N=1e6+10;
int head[N<<1],to[N<<1],st[N][50],nxt[N<<1],tot,dfn[N],low[N],cnt,Stack[N],times,top,n,m,q,father[N],deep[N];
vector<int> Tree[N];
void add(int u,int v){
nxt[++tot]=head[u];
head[u]=tot;
to[tot]=v;
}
void tarjan(int u){
low[u]=dfn[u]=++times;
Stack[++top]=u;
for(int i=head[u];i;i=nxt[i]){
int v=to[i];
if(!dfn[v]){
tarjan(v);
low[u]=min(low[u],low[v]);
if(low[v]==dfn[u]){
++cnt;
for(int x=0;x!=v;--top){
x=Stack[top];
Tree[cnt].push_back(x);
Tree[x].push_back(cnt);
}
Tree[cnt].push_back(u);
Tree[u].push_back(cnt);
}
}else{
low[u]=min(low[u],dfn[v]);
}
}
}
void dfs(int u,int fa){
st[u][0]=fa;
for(int i=1;i<=20;i++){
st[u][i]=st[st[u][i-1]][i-1];
}
for(int i=0;i<Tree[u].size();i++){
int v=Tree[u][i];
if(v==fa){
continue;
}
father[v]=u;
deep[v]=deep[u]+1;
dfs(v,u);
}
}
int lca(int u,int v){
if(deep[u]<deep[v]){
swap(u,v);
}
for(int i=30;i>=0;i--){
if(deep[st[u][i]]>=deep[v]){
u=st[u][i];
}
}
if(u==v){
return u;
}
for(int i=20;i>=0;i--){
if(st[u][i]!=st[v][i]){
u=st[u][i];
v=st[v][i];
}
}
return st[u][0];
}
void init(){
memset(head,0,sizeof(head));
memset(dfn,0,sizeof(dfn));
memset(low,0,sizeof(low));
memset(st,0,sizeof(st));
memset(father,0,sizeof(father));
memset(deep,0,sizeof(deep));
memset(to,0,sizeof(to));
memset(nxt,0,sizeof(nxt));
tot=times=top=cnt=0;
for(int i=0;i<N;i++){
Tree[i].clear();
}
}
int main(){
// init();
cin>>n>>m;
cnt=n;
for(int i=1;i<=m;i++){
int u,v;
cin>>u>>v;
add(u,v);
add(v,u);
}
// cout<<"Pass"<<endl;
for(int i=1;i<=n;i++){
if(!dfn[i]){
tarjan(i);
--top;
}
}
// for(int i=1;i<=cnt;i++){
// for(int j=0;j<Tree[i].size();j++){
// cout<<Tree[i][j]<<" ";
// }
// cout<<endl;
// }
// cout<<endl;
// cout<<"Pass"<<endl;
deep[1]=1;
dfs(1,0);
// cout<<"Pass"<<endl;
cin>>q;
while(q--){
int u,v;
cin>>u>>v;
int LCA=lca(u,v);
int dis=deep[u]+deep[v]-2*deep[LCA];
cout<<dis/2+1<<endl;
}
return 0;
}
}
int main(){
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
WYL::main();
return 0;
}
本文作者:Chillturtle
本文链接:https://www.cnblogs.com/OluMel/p/18498513
版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议进行许可。





【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步