【机器学习】线性回归
1.概念
线性回归(Linear Regression)是一种通过属性的线性组合来进行预测的线性模型,其目的是找到一条直线或者一个平面或者更高维的超平面,使得预测值与真实值之间的误差最小化。
通俗解释:
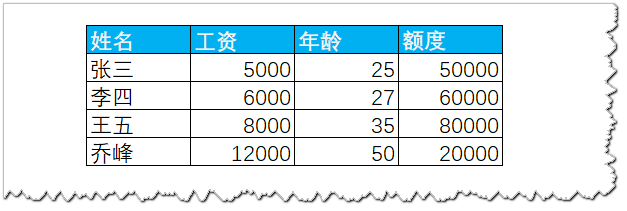
举个例子,银行现在有很多贷款客户,这些客户在贷款的时候,银行保存了他们的年龄、工资月收入、资产信息(是否有房、有车、理财产品等),那么我们称这这些信息为特征值。假如我现在去银行贷款,那么银行就可以通过已有客户的这些特征信息建立数据模型来预测我在该银行到底能贷多少钱。这里的数据模型指的就是线性回归。
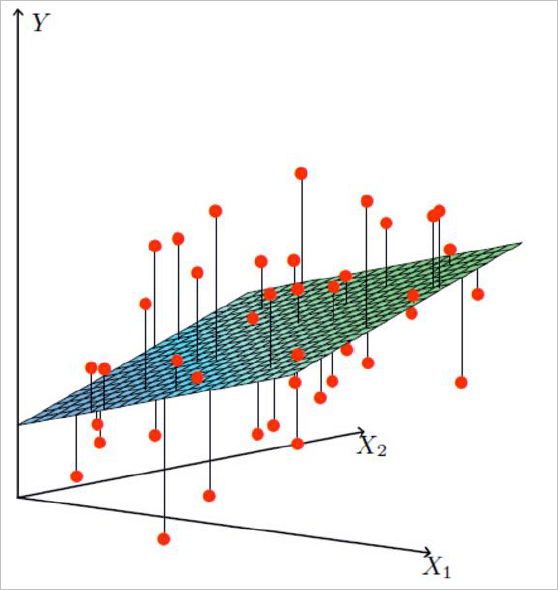
假设X1表示工资,X2表示年龄,那么Y就表示银行可以给我贷款的额度。这样我们就可以拟合出一条曲线,如下图
图1
2.理论
2.1 利用矩阵知识对线性公式整合
假设$\theta_1$是年龄,$\theta_2$是工资,那么拟合的平面为:

我们可以假定上述$\theta_0$使我们构建的虚拟特征值,其值全部为1,如下图:
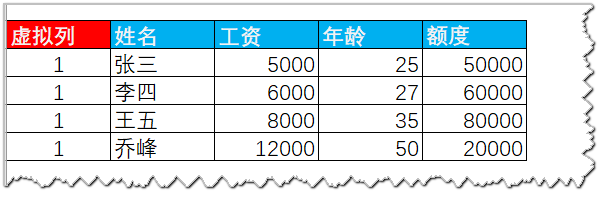
那么$\theta_0$与1的乘积永远是$\theta_0$,所以上述式子可以写成:
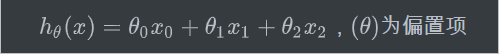
将式子简化后,得到(第二个等式是根据矩阵乘法转换后得到)

2.2 误差项分析
(1)真实值和预测值之间肯定是要存在差异的(用$\varepsilon$来表示误差)
(2)对于每个样本,存在以下公式
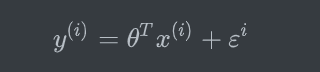
通俗解释:每个人去银行贷款的时候,有的人贷的多,有的人贷的少,预测值与真实值之间都会存在一些差距的。上面公式(2)的意思是,针对去银行贷款的每个客户,银行都会给他一个贷款额度,也就是公式中的$ y^{(i)} $,那么 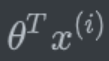
表示权重参数与特征参数的组合,这个组合就是预测值,那么 $ \varepsilon^{i} $则是真实值与预测值之间的差距。这个误差有可能是正的,也有可能是负的。可以参照图1理解。
(3)误差$ \varepsilon^{i} $是独立并且具有相同的分布,并且服从均值为0方差为$ \theta^2 $的高斯分布
- 独立:每一个样本都是独立的。例如:去银行贷款的人,是独立的,银行并不会因为他是皇亲国戚就多给他贷款
- 同分布:这里所谓的同分布指的是,研究的个体必须来自同一个地方,好比我们现在研究建设银行的贷款,我们不能一半用建设银行的客户,一半用工商银行的客户,那将毫无意义。
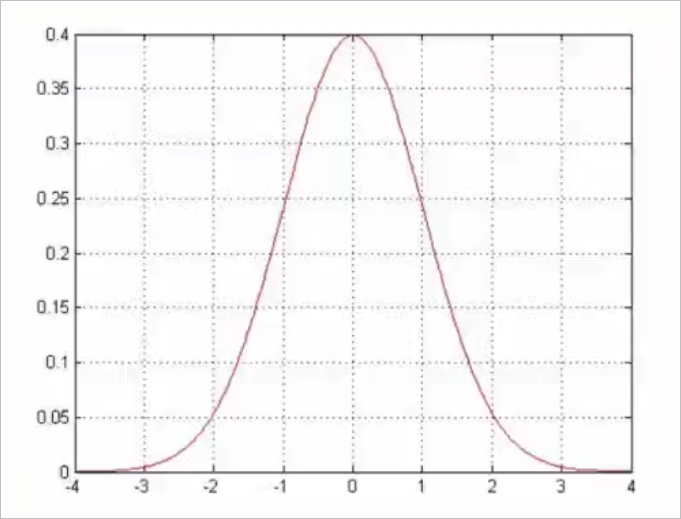
- 高斯分布:高斯分布也是正态分布。银行给每个客户的贷款额度不一样,有可能张三多点,李四多点,在实际情况下,银行不可能给每个人都多贷款,也不可能给每个人都少贷。多贷跟少贷的客户在绝大多数情况下,都是分布差不多的。高斯分布就是指在绝大多数情况下,在均值附近浮动不会太大,极小情况下浮动会比较大。从下图可以看出
2.3 似然函数的理解
推导:
预测值与误差的公式如下:
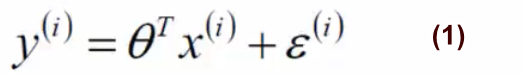
由于误差服从高斯分布:
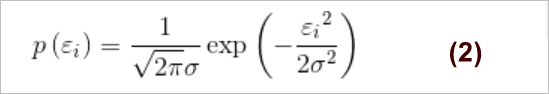
将(1)带入到(2),得到:
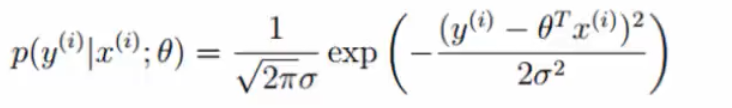
(4)似然函数:
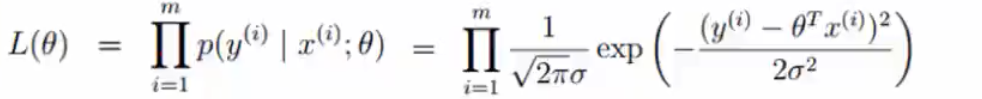
解释:举个例子,好多人喜欢买彩票,假如我也想去买彩票,那么我就会先找几个人打听打听,此处假如我找了10个人打听,有8个人都说买了中奖了,所以为就认为我的中奖率为80%。说白了就是什么样的参数跟我们的数据组合后恰好是真实值。
(5)对数函数:
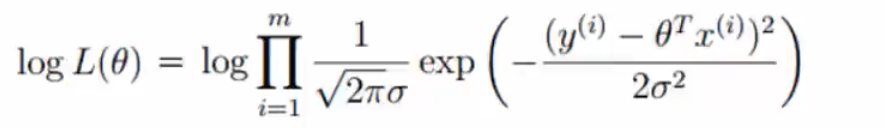
解释:在似然函数中,是基于乘法计算的,根据$logAB=logA+logB$,可以将似然函数转化为对数函数
展开化简:
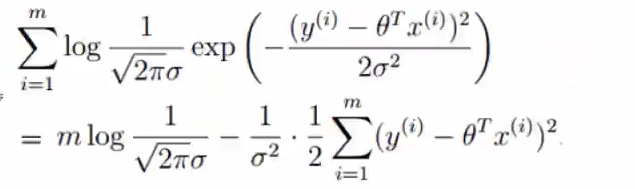
目标函数:那么似然函数极大估计(极大似然函数),所以让似然函数越大越好,得到下式
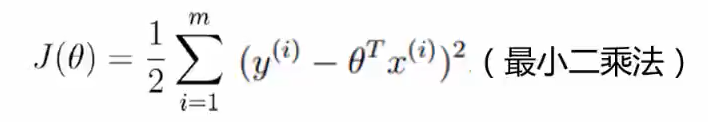
这就是最小二乘法的推导公式。
2.4 线性回归求解
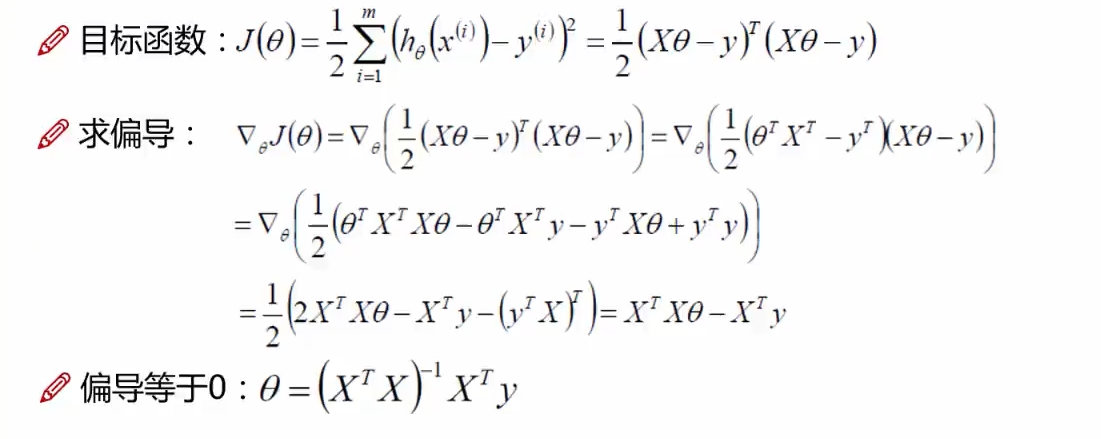
2.5 评估方法

声明:书写博客不易,转载请注明出处,请支持原创,侵权将追究法律责任
个性签名:人的一切的痛苦,本质上都是对自己无能的愤怒
如果觉得这篇文章对你有小小的帮助的话,记得在右下角点个“推荐”哦,博主在此感谢!

