CF487E Tourists 题解
思路分析
看到这道题首先想到的此题的树上版本。(不就是树链剖分的板子题么?)
但是此题是图上的两点间的走法,自然要想到是圆方树。
我们先无脑构建出圆方树。
我们先猜测:设后加入的节点权值为 inf,直接再圆方树上做述链剖分?
看上去很简单,但是完全不对,考虑同一个点双的情况。
他们在圆方树中是兄弟的关系,根本剖不到上面去,但是同样对答案有贡献。
所以不能树链剖分去做? NO!
我们来模拟一下这组数据:
n = 10 m = 11
1 2
2 3
1 4
3 4
4 5
5 6
4 7
6 7
6 9
6 10
9 10
接下来给出原图和原图相对应的圆方图:
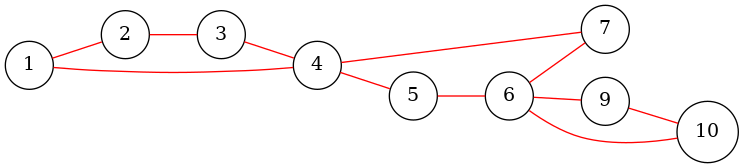
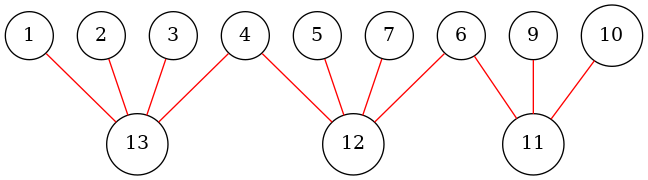
有一个大胆的设想:因为每一个新建的方形节点都对应一个点双,是不是可以把新建的节点权值更新成和它相连的所有节点权值的最小值呢?
好像不对呀,要是像途中 \(4\) 节点一样怎么办啊,一旦向左走就出不去了。
其实根本不要这么担心,仔细模拟一下发现:会出现上面这种情况的点对路径不会经过 \(13\) ! (看来是想多了)
于是我们得到以下思路:
- 先构建出圆方树。
- 每个新节点为与它相连的节点的权值最小值。
- 树链剖分,每次修改时更新对应的新节点。
看上去非常完美,结果 TLE 在了第 \(18\) 个点。
来看下面的一个图:(你就会怀疑人生)
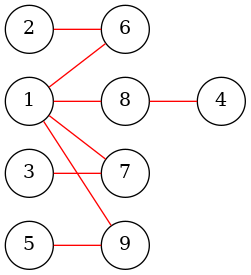
此时我们的 \(n=5\),这个图还有个名字——菊花图,成功把我们卡到了 \(O(n^2)\)。
那么我们之前的要推翻重来吗?不是我们来考虑圆方树的性质。
因为圆方树就是树,我们直接从树的性质入手。
考虑到每个树上节点只会有一个父亲,那么我们可以把一个方节点记录其子节点的最小值。
所以有什么区别么?有!这样的话我们每个更新就从他的所连接点变成了父亲节点!
我们对每一个方形节点建一棵平衡树,维护一下最小值。(我用的是 \(multiset\))
注意:当两个节点的 \(lca\) 是方形节点时,要考虑方形节点的的父亲节点。
Code
代码还是很清新的 \tuu
#include <bits/stdc++.h>
#define file(a) freopen(a".in", "r", stdin), freopen(a".out", "w", stdout)
#define Enter putchar('\n')
#define quad putchar(' ')
namespace IO {
template <class T> inline void read(T &a);
template <class T, class ...rest> inline void read(T &a, rest &...x);
template <class T> inline void write(T x);
template <class T, class ...rest> inline void write(T x, rest ...a);
}
#define N 200005
int n, m, Q, w[N], ww[N];
int tot2, head2[N], to2[N], then2[N], val2[N];
int tot, head[2 * N], to[2 * N], then[2 * N], val[2 * N];
int dfn[N], low[N], tp, sta[N], dfnnum, cnt;
int ff[N][30];
int seg[N], rev[4 * N], siz[N], son[N], top[N], dep[N], fa[N], mn[4 * N];
char c[3];
std::multiset <int> st[N];
inline void addline(int x, int y) {
tot ++;
to[tot] = y;
then[tot] = head[x];
head[x] = tot;
}
inline void addline2(int x, int y) {
tot2 ++;
to2[tot2] = y;
then2[tot2] = head2[x];
head2[x] = tot2;
}
inline void tarjan(int now) {
dfn[now] = low[now] = ++dfnnum;
sta[++tp] = now;
for (int i = head2[now]; i; i = then2[i]) {
int t = to2[i];
if (!dfn[t]) {
tarjan(t);
low[now] = std::min(low[now], low[t]);
if (low[t] == dfn[now]) {
++cnt;
while (tp && sta[tp] != t) {
addline(cnt, sta[tp]);
addline(sta[tp], cnt);
tp--;
}
addline(cnt, sta[tp]);
addline(sta[tp], cnt);
tp--;
addline(now, cnt);
addline(cnt, now);
}
} else
low[now] = std::min(low[now], dfn[t]);
}
}
inline int LCA(int x, int y) {
if (dep[x] < dep[y]) std::swap(x, y);
for (int i = 20;i >= 0; i--)
if (dep[ff[x][i]] >= dep[y])
x = ff[x][i];
if (x == y) return x;
for (int i = 20; i >= 0; i--)
if (ff[x][i] != ff[y][i])
x = ff[x][i], y = ff[y][i];
return ff[x][0];
}
namespace Segt {
inline void dfs1(int now, int father);
inline void dfs2(int now, int father);
inline void build(int k, int l, int r);
inline void modify(int k, int l, int r, int pos, int val);
inline int query(int k, int l, int r, int x, int y);
inline int solve(int x, int y);
}
signed main(void) {
// file("CF487E");
IO::read(n, m, Q);
for (int i = 1; i <= n; i++) IO::read(w[i]);
for (int i = 1, x, y; i <= m; i++) {
IO::read(x, y);
addline2(x, y); addline2(y, x);
}
cnt = n;
for (int i = 1; i <= n; i++)
if (!dfn[i]) tarjan(i), tp--;
// for (int i = 1; i <= cnt; i++) {
// for (int j = head[i]; j; j = then[j])
// printf ("%d %d\n", i, to[j]);
// }
Segt::dfs1(1, 0);
for (int i = n + 1; i <= cnt; i++) {
w[i] = 0x3f3f3f3f;
for (int j = head[i]; j; j = then[j]){
if (dep[to[j]] > dep[i]) {
st[i].insert(w[to[j]]);
w[i] = std::min(w[i], w[to[j]]);
}
}
}
for (int i = 1; i <= cnt; i++)
ww[i] = w[i];
seg[0] = seg[1] = top[1] = rev[1] = 1;
Segt::dfs2(1, 0);
Segt::build(1, 1, seg[0]);
for (int test = 1, a, b; test <= Q; test++) {
scanf("%s", c + 1);
IO::read(a, b);
if (c[1] == 'C') {
int last = ww[a];
ww[a] = b;
Segt::modify(1, 1, seg[0], seg[a], b);
if (fa[a] == 0) continue;
// printf ("!");
int father = fa[a];
st[father].erase(last);
st[father].insert(b);
ww[father] = *st[father].begin();
Segt::modify(1, 1, seg[0], seg[father], ww[father]);
} else {
int lca = LCA(a, b);
// printf("%d %d %d\n", lca, fa[lca], ww[lca]);
int ans = Segt::solve(a, b);
if (lca > n)
ans = std::min(ans, ww[fa[lca]]);
IO::write(ans);
Enter;
}
}
}
namespace Segt {
inline void dfs1(int now, int father) {
siz[now] = 1;
fa[now] = father;
ff[now][0] = father;
dep[now] = dep[father] + 1;
for (int i = 0; i < 25; i++)
ff[now][i + 1] = ff[ff[now][i]][i];
for (int i = head[now]; i; i = then[i]) {
int t = to[i];
if (t == father) continue;
dfs1(t, now);
siz[now] += siz[t];
if (siz[t] > siz[son[now]]) son[now] = t;
}
}
inline void dfs2(int now, int father) {
if (son[now]) {
seg[son[now]] = ++seg[0];
top[son[now]] = top[now];
rev[seg[0]] = son[now];
dfs2(son[now], now);
}
for (int i = head[now]; i; i = then[i]) {
int t = to[i];
if (top[t]) continue;
seg[t] = ++seg[0];
rev[seg[0]] = t;
top[t] = t;
dfs2(t, now);
}
}
inline void build(int k, int l, int r) {
if (l == r) {
mn[k] = w[rev[l]];
return ;
}
int mid = (l + r) / 2;
build(k * 2, l, mid);
build(k * 2 + 1, mid + 1, r);
mn[k] = std::min(mn[k * 2], mn[k * 2 + 1]);
}
inline void modify(int k, int l, int r, int pos, int val) {
if (pos > r || pos < l) return ;
if (l == r && l == pos) {
mn[k] = val;
return ;
}
int mid = (l + r) / 2;
if (mid >= pos) modify(k * 2, l, mid, pos, val);
if (mid < pos) modify(k * 2 + 1, mid + 1, r, pos, val);
mn[k] = std::min(mn[k * 2], mn[k * 2 + 1]);
}
inline int query(int k, int l, int r, int x, int y) {
if (x > r || y < l) return 0x3f3f3f3f;
if (l >= x && r <= y) return mn[k];
int mid = (l + r) / 2;
if (mid >= x) {
if (mid < y) {
int min1, min2;
min1 = query(k * 2, l, mid, x, y);
min2 = query(k * 2 + 1, mid + 1, r, x, y);
return std::min(min1, min2);
} else
return query(k * 2, l, mid, x, y);
} else
return query(k * 2 + 1, mid + 1, r, x, y);
}
inline int solve(int x, int y) {
int fx = top[x], fy = top[y];
int ret = 0x3f3f3f3f;
while (fx != fy) {
if (dep[fx] < dep[fy])
std::swap(x, y), std::swap(fx, fy);
ret = std::min(ret, query(1, 1, seg[0], seg[fx], seg[x]));
x = fa[fx]; fx = top[x];
}
if (dep[x] > dep[y]) std::swap(x, y);
ret = std::min(ret, query(1, 1, seg[0], seg[x], seg[y]));
return ret;
}
}
namespace IO {
template <class T> inline void read(T &a) {
T s = 0, t = 1;
char c = getchar();
while ((c < '0' || c > '9') && c != '-')
c = getchar();
if (c == '-')
c = getchar(), t = -1;
while (c >= '0' && c <= '9')
s = (s << 1) + (s << 3) + (c ^ 48), c = getchar();
a = s * t;
}
template <class T, class ...rest> inline void read(T &a, rest &...x) {
read(a); read(x...);
}
template <class T> inline void write(T x) {
if (x == 0) putchar('0');
if (x < 0) putchar('-'), x = -x;
int top = 0, sta[50] = {0};
while (x)
sta[++top] = x % 10, x /= 10;
while (top)
putchar(sta[top] + '0'), top --;
return ;
}
template <class T, class ...rest> inline void write(T x, rest ...a) {
write(x); quad; write(a...);
}
}


