圆方树学习笔记

前言#

模拟赛要求图上距离为 $k$ 的节点对数，就学了一下圆方树
众所周知，树有很多美妙的性质，但是有些题目非把树上问题搬到图上，这时我们就要上圆方树了。
那么圆方树是什么呢？(是圆形节点和方形节点构成的树)
圆方树（$Blockforest$ 或 $Round-squaretree$）1就是一种将图变成树的方法。本文将介绍圆方树的构建，性质和一些应用。

定义#

圆方树一开始是为“仙人掌”定制的。（每条边在不超过一个简单环中的无向图）
但是现在发现我们也可以在一般图中使用它。

前置知识：点双联通分量。#

割点的定义：在一个图中，如果把一个节点 $i$ 删除后，原图不再联通，那么我们称这个点是割点。
点双联通分量的定义：当一个图中没有割点，当前图是点双联通分量。
我们用 $Tarjan$ 求出点双联通分量，在此不在累述。

而一个图的 点双连通分量 则是一个 极大点双连通子图。
性质：与强连通分量等不同，一个点可能属于多个点双，但是一条边属于恰好一个点双。
那么在圆方树中，每一个原来的节点我们用圆形的点表示，每一个点双用方点表示。
给大家放几个图感受一下：

（图片来自 oi-wiki.org）

圆方树的节点个数小于等于原来节点的两倍，原因很简单，因为原图的点割点的个数最坏情况下也最多有 $N$ 个，所以做题时注意数组要开两倍大小。

构建圆方树#

因为原图中有多少个联通分量就有多少个圆方树，所以我们设原图就是连通图。
因为圆方树的构建和点双联通分量有关，所以我们直接调用 $Tarjan$ 搞出割点就可以啦。

根据 $Tarjan$ 算法：
每一个 low[i] 表示当前 $i$ 节点最多一次返祖边或向父亲的树边 能访问到的点的最小 DFS 序。
稍微构建一个图模拟一下就可以发现，对于每一个点双联通分量，都是原图中对应的一个环，且每一条树边恰好被分在一个点双中，对于一个点双中最靠上的节点，满足 $df{n}_i=lo{w}_i$ 的性质。
记录一个栈，存储还未确定所属点双（可能有多个）的节点。（和 $Tarjan$ 一样）
对于每一个从栈弹出的节点，我们让它和新建的节点相连接。记得最后要和 $u$ 相连。
如图所示：（无加粗的是新加入的方形节点）

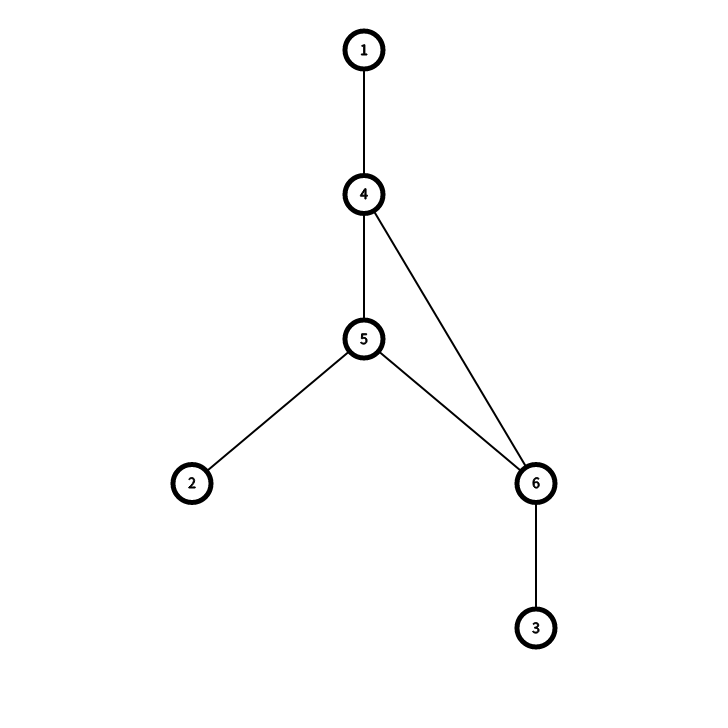
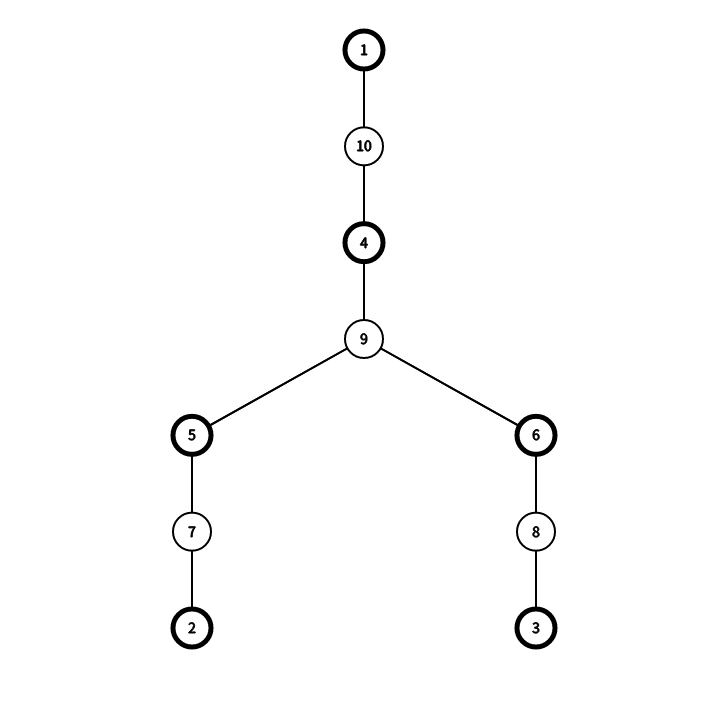
Code#

// addline 为圆方树的边
// head2, to2.... 为原图的边
inline void tarjan(int now) {
  dfn[now] = low[now] = ++dfnnum;
  sta[++top] = now;
  for (int i = head2[now]; i; i = then2[i]) {
    int t = to2[i];
    if (!dfn[t]) {
      tarjan(t);
      low[now] = std::min(low[now], low[t]);
      if (low[t] == dfn[now]) {
        ++cnt;
        while (top && sta[top] != t) {
          addline(cnt, sta[top]);
          addline(sta[top], cnt);
          top--;
        }
        addline(cnt, sta[top]);
        addline(sta[top], cnt);
        top--;
        addline(now, cnt);
        addline(cnt, now);
      }
    } else
      low[now] = std::min(low[now], dfn[t]);
  }
}

例题#

P4630 [APIO2018] Duathlon 铁人两项
CF487E Tourists