【LeetCode】20.动态规划系列——子序列

总目录：

LeetCode系列导航目录

 

0.理论基础

0.1.题型

0.2.要点

子序列：不连续的、不改变相对顺序的子集

子数组：连续的子集

0.3.代码实例

这一类题往往需要画dp表，从而找出状态转移公式。

回文部分要重点练习：双指针+dp

 

1.最长递增子序列

1.1.问题描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。
子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
链接：https://leetcode.cn/problems/longest-increasing-subsequence

1.2.要点

思想：经常反省过往，当时机来临时在过往最好的状态上再上一层楼

转移公式：if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);

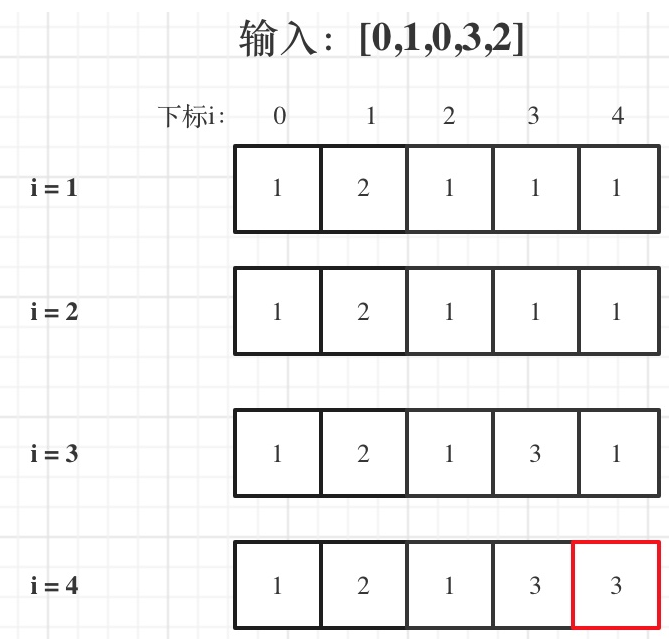
1.3.代码实例

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int len=nums.size();
        if(len<=1){
            return len;
        }
        int ret=0;

        vector<int> dp(len,1);//dp[i],到第i项时包含nums[i]的最长子序列
        for(int i=1;i<len;i++){
            //经常反省过往
            for(int j=0;j<i;j++){
                //当机会来临时，在过往最好状态上更上一层楼
                if(nums[i]>nums[j]){
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }

            ret=dp[i]>ret?dp[i]:ret;
        }

        //这里不能返回dp[len-1],因为最长子序列可能不以最后一个元素结尾
        return ret;
    }
};

 

2.最长连续递增序列

2.1.问题描述

给定一个未经排序的整数数组，找到最长且 连续递增的子序列，并返回该序列的长度。
连续递增的子序列 可以由两个下标 l 和 r（l < r）确定，如果对于每个 l <= i < r，都有 nums[i] < nums[i + 1] ，那么子序列 [nums[l], nums[l + 1], ..., nums[r - 1], nums[r]] 就是连续递增子序列。
链接：https://leetcode.cn/problems/longest-continuous-increasing-subsequence

2.2.要点

思想：比前一步大则+1，使用全局变量来维护最大值

状态转移：if(nums[i]>nums[i-1]) dp[i]=max(dp[i],dp[i-1]+1);

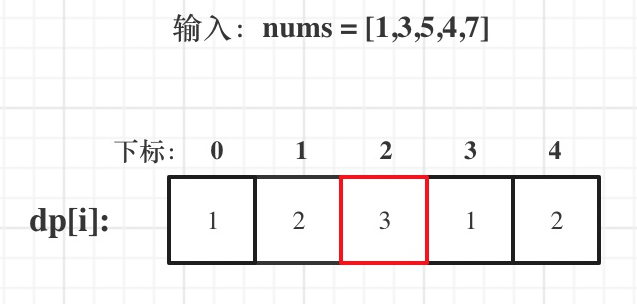
2.3.代码实例

class Solution {
public:
    int findLengthOfLCIS(vector<int>& nums) {
        int len=nums.size();
        if(len<=1){
            return len;
        }

        int ret=1;
        vector<int> dp(len,1);
        for(int i=1;i<len;i++){
            //只回头看1步，可以的话就更上一层楼
            if(nums[i]>nums[i-1]){
                dp[i]=max(dp[i],dp[i-1]+1);
            } 
            ret=max(dp[i],ret);
        }

        return ret;
    }
};

 

3.最长重复子数组

3.1.问题描述

给两个整数数组 nums1 和 nums2 ，返回 两个数组中 公共的 、长度最长的子数组的长度 。

链接：https://leetcode.cn/problems/maximum-length-of-repeated-subarray/

3.2.要点

子数组：连续的子集

状态转移:if(nums1[i]==nums2[j]) dp[i][j]=dp[i-1][j-1]+1;

只关注nums1[i]==nums2[j]

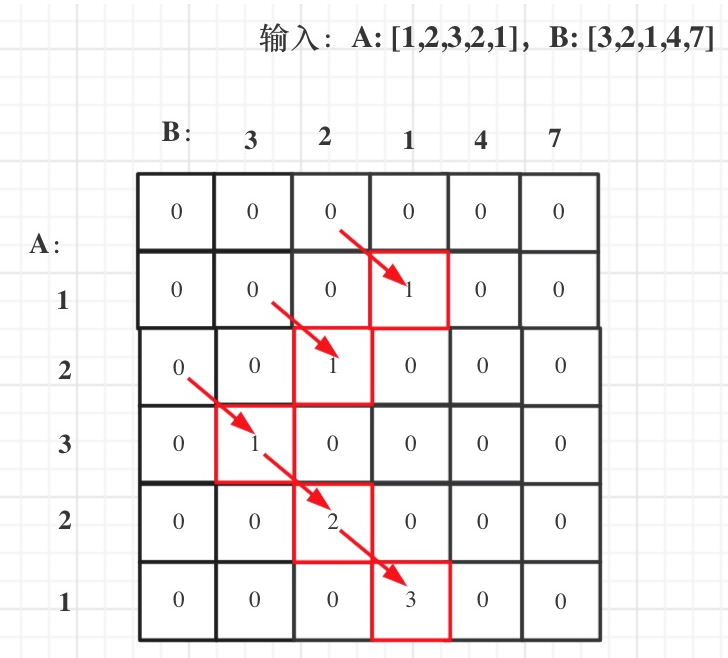
3.3.代码实例

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        if(len1==0||len2==0){
            return 0;
        }

        int ret=0;
        //dp[i][j],以nums1[i]和nums2[j]结尾的公共子数组长度,子数组是连续的，如果求子序列是不连续的        
        vector<vector<int>> dp(len1,vector<int>(len2,0));

        for(int i=0;i<len1;i++){
            for(int j=0;j<len2;j++){                
                if(nums1[i]!=nums2[j]){
                    continue;                   
                }

                if(i<1||j<1){
                    dp[i][j]=1;
                }
                else{
                    dp[i][j]=dp[i-1][j-1]+1;
                } 
                ret=max(ret,dp[i][j]);
            }            
        }

        return ret;
    }
};

 

4.最长公共子序列

4.1.问题描述

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。
一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。
例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。
链接：https://leetcode.cn/problems/longest-common-subsequence

4.2.要点

主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同

如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1;

如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列，取最大的。

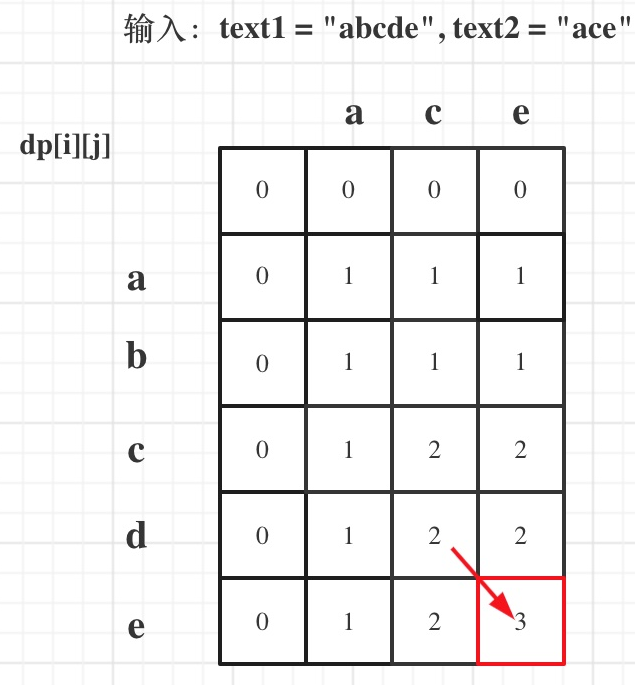
4.3.代码实例

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
        int len1=text1.length();
        int len2=text2.length();
        if(len1<=0||len2<=0){
            return 0;
        }

        int ret=0;
        //dp[i][j],text1的[0,i-1]与text2的[0,j-1]之间的公共子序列长度
        vector<vector<int>> dp(len1+1,vector(len2+1,0));
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(text1[i-1]!=text2[j-1]){
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);                    
                }
                else{
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                ret=max(ret,dp[i][j]);
            }
        }

        return ret;
    }
};

 

5.不相交的线

5.1.问题描述

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：
（1）nums1[i] == nums2[j]
（2）且绘制的直线不与任何其他连线（非水平线）相交。
请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。
以这种方法绘制线条，并返回可以绘制的最大连线数。
链接：https://leetcode.cn/problems/uncrossed-lines

5.2.要点

同上，最长公共子序列问题

5.3.代码实例

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int len1=nums1.size();
        int len2=nums2.size();
        if(len1<1||len2<1){
            return 0;
        }

        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(nums1[i-1]==nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1;
                }
                else{
                    dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
                }
            }
        }


        return dp[len1][len2];
    }
};

 

6.最大子数组和

6.1.问题描述

给你一个整数数组 nums ，请你找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

子数组 是数组中的一个连续部分。

链接：https://leetcode.cn/problems/maximum-subarray/

6.2.要点

将累加和同当前值本身作比较，以便处理前序累加和为负的情况。

状态转移：dp[i] = max(dp[i - 1] + nums[i], nums[i]);

6.3.代码实例

class Solution {
public:
    int maxSubArray(vector<int>& nums) {
        int len=nums.size();
        if(len==0){
            return 0;
        }
        if(len==1){
            return nums[0];
        }

        int maxSum=nums[0];
        vector<int> dp(len,0);//dp[i],以nums[i]结尾的连续数组最大和
        dp[0]=nums[0];
        for(int i=1;i<len;i++){
            if(dp[i-1]<=0){
                dp[i]=nums[i];
            }
            else{
                dp[i]=dp[i-1]+nums[i];
            }
            maxSum=max(maxSum,dp[i]);
        }

        return maxSum;
    }
};

 

7.判断子序列

7.1.问题描述

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。
字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。
链接：https://leetcode.cn/problems/is-subsequence

7.2.要点

判断最长子序列的长度是否等于s的长度

if (s[i - 1] == t[j - 1])，那么dp[i][j] = dp[i - 1][j - 1] + 1;

if (s[i - 1] != t[j - 1])，那么dp[i][j] = dp[i][j - 1];

注：也可以用bool类型的dp表

7.3.代码实例

class Solution {
public:
    bool isSubsequence(string s, string t) {
        vector<vector<int>> dp(s.size() + 1, vector<int>(t.size() + 1, 0));
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
                else dp[i][j] = dp[i][j - 1];
            }
        }
        if (dp[s.size()][t.size()] == s.size()) return true;
        return false;
    }
};

 

8.不同的子序列

8.1.问题描述

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。
字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）
链接：https://leetcode.cn/problems/distinct-subsequences

8.2.要点

特定题型，研究dp表得出

s[i - 1] 与 t[j - 1]相等时，dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];

s[i - 1] 与 t[j - 1]不相等时，dp[i][j] = dp[i - 1][j];

8.3.代码实例

class Solution {
public:
    int numDistinct(string s, string t) {
        int len1=s.length();
        int len2=t.length();
        if(len1<len2){
            return false;
        }

        //dp[i][j]，s以i-1截止，t以j-1截止的子序列数量
        vector<vector<uint64_t>> dp(s.size() + 1, vector<uint64_t>(t.size() + 1, 0));
        dp[0][0]=1;
        for (int i = 0; i <= s.size(); i++) dp[i][0] = 1;
        for (int j = 1; j <= t.size(); j++) dp[0][j] = 0;         
        for (int i = 1; i <= s.size(); i++) {
            for (int j = 1; j <= t.size(); j++) {
                if (s[i - 1] == t[j - 1]) 
                    dp[i][j] = dp[i - 1][j - 1] + dp[i-1][j];
                else 
                    dp[i][j] = dp[i-1][j];
            }
        }
        return dp[len1][len2];
    }
};

 

9.两个字符串的删除操作

9.1.问题描述

给定两个单词 word1 和 word2 ，返回使得 word1 和  word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

链接：https://leetcode.cn/problems/delete-operation-for-two-strings/

9.2.要点

分i、j是否相同

当word1[i - 1] 与 word2[j - 1]相同的时候，dp[i][j] = dp[i - 1][j - 1];

当word1[i - 1] 与 word2[j - 1]不相同的时候，有三种情况：

（1）删word1[i - 1]，最少操作次数为dp[i - 1][j] + 1

（2）删word2[j - 1]，最少操作次数为dp[i][j - 1] + 1

（3）同时删word1[i - 1]和word2[j - 1]，操作的最少次数为dp[i - 1][j - 1] + 2

那最后当然是取最小值，所以当word1[i - 1] 与 word2[j - 1]不相同的时候，递推公式：dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1});

9.3.代码实例

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.length();
        int len2=word2.length();

        vector<vector<int>> dp(len1 + 1, vector<int>(len2 + 1));
        for (int i = 0; i <= len1; i++) dp[i][0] = i;//有几个删几个
        for (int j = 0; j <= len2; j++) dp[0][j] = j;//有几个删几个
        for (int i = 1; i <= len1; i++) {
            for (int j = 1; j <= len2; j++) {
                if (word1[i - 1] == word2[j - 1]) {
                    //相等时可忽略，看一下都退一步的数值
                    dp[i][j] = dp[i - 1][j - 1];
                } else {
                    //不相等时，要么a删、要么b删、要么ab都删
                    dp[i][j] = min(min(dp[i - 1][j] + 1, dp[i][j - 1] + 1),dp[i-1][j-1]+2);
                }
            }
        }
        return dp[len1][len2];
    }
};

 

10.编辑距离

10.1.问题描述

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数  。
你可以对一个单词进行如下三种操作：
（1）插入一个字符
（2）删除一个字符
（3）替换一个字符
链接：https://leetcode.cn/problems/edit-distance

10.2.要点

if (word1[i - 1] == word2[j - 1]) 那么说明不用任何编辑，dp[i][j] 就应该是 dp[i - 1][j - 1]，即dp[i][j] = dp[i - 1][j - 1];

当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

可能的操作：

（1）word1删除1个，等价于word2增加1个；

（2）word2删除1个，等价于word1增加1个；

（3）word1或word2替换1个使word1[i - 1] == word2[j - 1]

10.3.代码实例

class Solution {
public:
    int minDistance(string word1, string word2) {
        int len1=word1.length();
        int len2=word2.length();

        //dp[i][j],以i-1结束的word1和以j-1结束的word2的最小操作数
        vector<vector<int>> dp(len1+1,vector<int>(len2+1,0));
        for (int i = 0; i <= len1; i++) dp[i][0] = i;
        for (int j = 0; j <= len2; j++) dp[0][j] = j;
        dp[0][0]=0;
        for(int i=1;i<=len1;i++){
            for(int j=1;j<=len2;j++){
                if(word1[i-1]==word2[j-1]){
                    dp[i][j]=dp[i-1][j-1];
                }
                else{
                    dp[i][j]=min(min(dp[i-1][j]+1,dp[i][j-1]+1),dp[i-1][j-1]+1);
                }
            }
        }

        return dp[len1][len2];
    }
};

 

11.回文子串

11.1.问题描述

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串，即使是由相同的字符组成，也会被视作不同的子串。
链接：https://leetcode.cn/problems/palindromic-substrings

11.2.要点

特殊顺序的dp表

s[i]与s[j]相等，s[i]与s[j]不相等这两种。

当s[i]与s[j]不相等，那没啥好说的了，dp[i][j]一定是false。

当s[i]与s[j]相等时，这就复杂一些了，有如下三种情况

• 情况一：下标i 与 j相同，同一个字符例如a，当然是回文子串
• 情况二：下标i 与 j相差为1，例如aa，也是回文子串
• 情况三：下标：i 与 j相差大于1的时候，例如cabac，此时s[i]与s[j]已经相同了，我们看i到j区间是不是回文子串就看aba是不是回文就可以了，那么aba的区间就是 i+1 与 j-1区间，这个区间是不是回文就看dp[i + 1][j - 1]是否为true。

if (s[i] == s[j]) {
    if (j - i <= 1) { // 情况一 和 情况二
        result++;
        dp[i][j] = true;
    } else if (dp[i + 1][j - 1]) { // 情况三
        result++;
        dp[i][j] = true;
    }
}

11.3.代码实例

class Solution {
public:
    int countSubstrings(string s) {
        //dp[i][j],s[i,j]是否是回文字符串
        vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
        int result = 0;
        for (int i = s.size() - 1; i >= 0; i--) {  // 注意遍历顺序
            for (int j = i; j < s.size(); j++) {
                if(s[i]!=s[j]){
                    continue;
                }
                
                //s[i]!=s[j]
                if (j - i <= 1) { // 情况一 和 情况二
                    result++;
                    dp[i][j] = true;
                } else if (dp[i + 1][j - 1]) { // 情况三
                    result++;
                    dp[i][j] = true;
                }
            }
        }
        return result;
    }
};

 

12.最长回文子序列

12.1.问题描述

给你一个字符串 s ，找出其中最长的回文子序列，并返回该序列的长度。
子序列定义为：不改变剩余字符顺序的情况下，删除某些字符或者不删除任何字符形成的一个序列。
链接：https://leetcode.cn/problems/longest-palindromic-subsequence

12.2.要点

子序列可以不连续

相等不相等、间距是否小于等于1以便收缩的不同情况

如果s[i]与s[j]相同，那么dp[i][j] = dp[i + 1][j - 1] + 2;

如果s[i]与s[j]不相同，说明s[i]和s[j]的同时加入 并不能增加[i,j]区间回文子串的长度，那么分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);

12.3.代码实例

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int len=s.length();
        if(len<=1){
            return len;
        }
        
        //dp[i][j],s[i][j]之中最长回文子序列的长度
        vector<vector<int>> dp(len,vector<int>(len,0));

        for(int i=len-1;i>=0;i--){
            for(int j=i;j<len;j++){
                if(j-i<=1){
                    if(s[i]==s[j]){
                        dp[i][j]=j-i+1;                        
                    }
                    else{
                        dp[i][j]=1;
                    }                    
                }
                else{
                    if(s[i]==s[j]){
                        dp[i][j]=dp[i+1][j-1]+2;
                    }
                    else{
                        dp[i][j]=max(max(dp[i+1][j],dp[i][j-1]),dp[i+1][j-1]);
                    }
                }
            }
        }

        return dp[0][len-1];
    }
};

 

xxx.问题

xxx.1.问题描述

111

xxx.2.要点

222

xxx.3.代码实例

333