【LeetCode】16.动态规划系列——基础

总目录：

LeetCode系列导航目录

 

0.理论基础

0.1.概念

算法基础——动态规划

Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。

所以动态规划中每一个状态一定是由上一个状态推导出来的，这一点就区分于贪心，贪心没有状态推导，而是从局部直接选最优的。

0.2.下手套路

（1）确定dp数组（dp table）以及下标的含义；

（2）确定递推公式；

（3）dp数组如何初始化；

（4）确定遍历顺序；

（5）举例推导dp数组进行验证，debug。

 

1.斐波那契数

1.1.问题描述

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
给定 n ，请计算 F(n) 。
链接：https://leetcode.cn/problems/fibonacci-number

1.2.要点

dp[n]含义：第n项斐波那契数

递推公式：已给出

遍历方式：递归或迭代都可

1.3.代码实例

class Solution {
public:
    int fib(int n) {
        if(n<=1){
            return n;
        }
        int a=0,b=1;
        for(int i=2;i<=n;i++){
            b+=a;
            a=b-a;
        }

        return b;
    }
};

 

2.爬楼梯

2.1.问题描述

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

链接：https://leetcode.cn/problems/climbing-stairs/

2.2.要点

dp[n]:到第n阶有多少种上楼方式

递推公式：要想到某台阶，取决于前面有哪些台阶可以一步到达这里。dp[n]=dp[n-1]+dp[n-2]

2.3.代码实例

class Solution {
public:
    int climbStairs(int n) {
        if(n<=2){
            return n;
        }

        int a=1,b=2;
        for(int i=3;i<=n;i++){
            b+=a;
            a=b-a;
        }

        return b;
    }
};

 

3.使用最小花费爬楼梯

3.1.问题描述

给你一个整数数组 cost ，其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用，即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
链接：https://leetcode.cn/problems/min-cost-climbing-stairs

3.2.要点

dp[n]:到达n处时的最小累计代价

递推公式：最小累计代价为前面能一步到达本处的那些台阶的(累计代价+当前台阶代价)序列的最小值。dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);

3.3.代码实例

class Solution {
public:
    int minCostClimbingStairs(vector<int>& cost) {
        int dataLen=cost.size();
        if(dataLen<2){
            return 0;
        }

        vector<int> dp(dataLen+1,0);
        for(int i=2;i<=dataLen;i++){
            dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }

        return dp.back();
    }
};

 

4.不同路径

4.1.问题描述

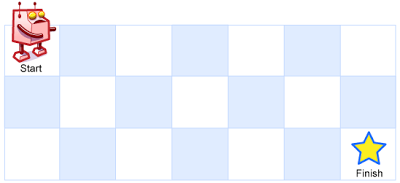
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。
问总共有多少条不同的路径？

链接：https://leetcode.cn/problems/unique-paths

 

4.2.要点

dp[m][n]:到达(m,n)处时的路径数量

递推公式：到达(m,n)处只能来自于(m-1,n)和(m,n-1)，所以dp[i][j]=dp[i-1][j]+dp[i][j-1];

4.3.代码实例

class Solution {
public:
    int uniquePaths(int m, int n) {
        if(m<=1||n<=1){
            return 1;
        }
        vector<vector<int>> dp(m,vector<int>(n,1));
        for(int i=1;i<m;i++){
            for(int j=1;j<n;j++){
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }

        return dp[m-1][n-1];
    }
};

 

5.不同路径——有障碍

5.1.问题描述

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？
网格中的障碍物和空位置分别用 1 和 0 来表示。

链接：https://leetcode.cn/problems/unique-paths-ii

5.2.要点

dp[m][n]:到达(m,n)处时的路径数量

递推公式：到达(m,n)处只能来自于(m-1,n)和(m,n-1)，所以dp[i][j]=dp[i-1][j]+dp[i][j-1];

注意：最上边的一行有障碍会造成右侧的都不可达，最左一列有障碍会造成下方的都不可达，起点或终点有障碍时肯定不可达。

5.3.代码实例

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int row=obstacleGrid.size();
        if(row==0){
            return 0;
        }        
        int col=obstacleGrid[0].size();
        if(col==0){
            return 0;
        }

        if(obstacleGrid[0][0]==1||obstacleGrid[row-1][col-1]==1){
            return 0;
        }

        //动态规划
        vector<vector<int>> dp(row,vector<int>(col,1));
        for(int i=0;i<row;i++){
            for(int j=0;j<col;j++){     
                if(obstacleGrid[i][j]==1){
                    dp[i][j]=0;

                    //如果是两条边缘
                    if(i==0){
                        for(int k=j;k<col;k++){
                            dp[i][k]=0;
                        }
                    }
                    if(j==0){
                        for(int k=i;k<row;k++){
                            dp[k][j]=0;
                        }
                    }
                    continue;
                }

                if(i==0||j==0){
                    continue;
                }
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }

        return dp[row-1][col-1];
    }
};

 

6.整数拆分，剪绳子问题，使乘积最大

6.1.问题描述

给定一个正整数 n ，将其拆分为 k 个 正整数 的和（ k >= 2 ），并使这些整数的乘积最大化。

返回 你可以获得的最大乘积 。

链接：https://leetcode.cn/problems/integer-break/

6.2.要点

dp[n]:n长的绳子切割得到的最大乘积

递推公式：对于n可以裁为i和n-i,对于n裁或者不裁、对于n裁了之后得到的i和n-i是否继续裁，取决于比较谁是最大值。

dp[n]=max(

dp[n],

i*(n-i),

i*dp[n-i],

dp[i]*(n-i),

dp[i]*dp[n-i])

6.3.代码实例

class Solution {
public:
    int integerBreak(int n) {
        vector<int> dp(n + 1, 0);
        dp[1] = 1;
        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i/2; j++) {
                //这里面包含了拆或者不拆、拆多长的抉择
                dp[i] = max(dp[i], (max(j, dp[j])) * (max(i - j, dp[i - j])));
            }
        }

        return dp[n];
    }
};

 

7.不同的二叉搜索树

7.1.问题描述

给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

链接：https://leetcode.cn/problems/unique-binary-search-trees/

7.2.要点

dp[n]:n个节点有多少种二叉搜索树构型

递推公式：特殊题型，卡特兰公式问题。

对于n个节点，每个节点都有当根节点的情况f(i)，dp[n]=f(1)+f(2)+...+f(n)

对于f(i)构成的搜索树中,其左子树有i-1个节点在构成dp[i-1]种搜索树，右边有n-i个节点构成的的dp[n-i]种搜索树，所以f(i)=dp[i-1]*dp[n-i]

综合以上可得dp[n]=dp[0]*dp[n-1]+dp[1]*dp[n-2]+...+dp[n-1]*dp[0],这就是卡特兰公式

7.3.代码实例

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n+1,0);
        dp[0]=1;
        dp[1]=1;
        for(int i=2;i<=n;i++){
            //dp[n]=dp[0]*dp[n-1]+dp[1]*dp[n-2]+...+dp[n-1]*dp[0]
            for(int j=1;j<=i;j++){
                dp[i]+=dp[j-1]*dp[i-j];
            }
        }

        return dp[n];
    }
};

 

 

 

xxx.问题

xxx.1.问题描述

111

xxx.2.要点

222

xxx.3.代码实例

333