【LeetCode】10.二叉树系列——属性

总目录：

LeetCode系列导航目录

1.判定对称二叉树

1.1.问题描述

给你一个二叉树的根节点 root ，检查它是否轴对称。

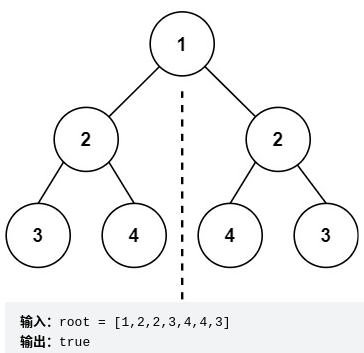
链接：https://leetcode.cn/problems/symmetric-tree/

1.2.要点

对称与否，一看是否都有/无节点，二看值是否相同

1递归

2迭代，用栈实现、用队列实现

1.3.代码实例

递归

 1 class Solution {
 2 public:
 3     bool isMirrored(TreeNode* leftNode,TreeNode* rightNode){
 4         //中止条件
 5         if((leftNode==NULL)!=(rightNode==NULL)){
 6             return false;
 7         }
 8         if(leftNode==NULL){
 9             return true;
10         }
11         if(leftNode->val!=rightNode->val){
12             return false;
13         }
14 
15         //调用递归
16         bool isOk=false;
17         isOk=isMirrored(leftNode->left,rightNode->right);
18         if(!isOk){
19             return false;
20         }
21         isOk=isMirrored(leftNode->right,rightNode->left);
22         if(!isOk){
23             return false;
24         }
25 
26         //能到这肯定是对称的，包括子树
27         return true;
28     }
29     bool isSymmetric(TreeNode* root) {
30         //中止条件
31         if(root==NULL){
32             return true;
33         }
34 
35         return isMirrored(root->left, root->right);
36     }
37 };

View Code

迭代+队列

 1 class Solution {
 2 public:
 3     bool isSymmetric(TreeNode* root) {
 4         if (root == NULL) return true;
 5         queue<TreeNode*> que;
 6         que.push(root->left);   // 将左子树头结点加入队列
 7         que.push(root->right);  // 将右子树头结点加入队列
 8         
 9         while (!que.empty()) {  // 接下来就要判断这两个树是否相互翻转
10             TreeNode* leftNode = que.front(); que.pop();
11             TreeNode* rightNode = que.front(); que.pop();
12             if (!leftNode && !rightNode) {  // 左节点为空、右节点为空，此时说明是对称的
13                 continue;
14             }
15 
16             // 左右一个节点不为空，或者都不为空但数值不相同，返回false
17             if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
18                 return false;
19             }
20             que.push(leftNode->left);   // 加入左节点左孩子
21             que.push(rightNode->right); // 加入右节点右孩子
22             que.push(leftNode->right);  // 加入左节点右孩子
23             que.push(rightNode->left);  // 加入右节点左孩子
24         }
25         return true;
26     }
27 };

View Code

迭代+栈

 1 class Solution {
 2 public:
 3     bool isSymmetric(TreeNode* root) {
 4         if (root == NULL) return true;
 5         stack<TreeNode*> st; // 这里改成了栈
 6         st.push(root->left);
 7         st.push(root->right);
 8         while (!st.empty()) {
 9             TreeNode* leftNode = st.top(); st.pop();
10             TreeNode* rightNode = st.top(); st.pop();
11             if (!leftNode && !rightNode) {
12                 continue;
13             }
14             if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
15                 return false;
16             }
17             st.push(leftNode->left);
18             st.push(rightNode->right);
19             st.push(leftNode->right);
20             st.push(rightNode->left);
21         }
22         return true;
23     }
24 };

View Code

2.完全二叉树的节点个数

2.1.问题描述

给你一棵完全二叉树的根节点 root ，求出该树的节点个数。
完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
链接：https://leetcode.cn/problems/count-complete-tree-nodes

2.2.要点

仍属于遍历范畴，方法任选

2.3.代码实例

迭代——层序遍历

 1 class Solution {
 2 public:
 3     int countNodes(TreeNode* root) {        
 4         if(root == NULL){
 5             return 0;
 6         }
 7 
 8         int nodeCnt=0;
 9         int nodeCntInQ=0;
10         queue<TreeNode*> q;
11         q.push(root);
12 
13         TreeNode* curNode=NULL;
14         while(!q.empty()){
15             nodeCntInQ=q.size();
16             nodeCnt+=nodeCntInQ;
17 
18             for(int i=0;i<nodeCntInQ;i++){
19                 curNode=q.front();
20                 q.pop();
21                 
22                 if(curNode->left) q.push(curNode->left);
23                 if(curNode->right) q.push(curNode->right);
24             }
25         }
26 
27         return nodeCnt;
28     }
29 };

View Code

3.判定平衡二叉树

3.1.问题描述

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

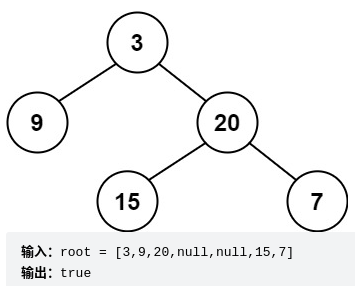
链接：https://leetcode.cn/problems/balanced-binary-tree

3.2.要点

1递归

深度搜索左右子树的最大深度，然后比较差值。

前、后序遍历都可。

3.3.代码实例

递归

 1 class Solution {
 2 public:
 3     int getDepth(TreeNode* root){
 4         if(root==NULL){
 5             return 0;
 6         }
 7 
 8         int leftDepth=getDepth(root->left);
 9         int rightDepth=getDepth(root->right);
10 
11         return max(leftDepth,rightDepth)+1;
12     }
13     bool isBalanced(TreeNode* root) {
14         if(root==NULL){
15             return true;
16         }
17 
18         int leftDepth=getDepth(root->left);
19         int rightDepth=getDepth(root->right);
20         if(abs(leftDepth-rightDepth)>1){
21             return false;
22         }
23 
24         bool isBalInLeft=isBalanced(root->left);
25         bool isBalInRight=isBalanced(root->right);
26 
27         return isBalInLeft&&isBalInRight;
28     }
29 };

View Code

4.二叉树的所有路径

4.1.问题描述

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

链接：https://leetcode.cn/problems/binary-tree-paths/

4.2.要点

路径需要累加，中间需要缓存前序路径，在走完一条路径之后又需要回溯。

注意在递归中回溯算法的技巧。递归中带着回溯

1向下递归

2向上递归

4.3.代码实例

向下递归

 1 class Solution {
 2 public:
 3     void recurve(TreeNode* root,string path,vector<string>& ret){
 4         path+=to_string(root->val);
 5         //如果是叶子节点
 6         if(root->left==NULL&&root->right==NULL){            
 7             ret.push_back(path);
 8             return;
 9         }
10 
11         if(root->left){            
12             recurve(root->left,path+"->",ret);
13         }
14         if(root->right){
15             recurve(root->right,path+"->",ret);
16         }
17     }
18 
19     vector<string> binaryTreePaths(TreeNode* root) {
20         vector<string> ret;
21         if(root==NULL){
22             return ret;
23         }
24 
25         recurve(root,"",ret);
26 
27         return ret;
28     }
29 };

View Code

向上递归,盖帽算法

 1 class Solution {
 2 public:
 3     vector<string> binaryTreePaths(TreeNode* root) {
 4         vector<string> res;
 5         if (root == NULL)
 6             return res;
 7         //到达叶子节点，把路径加入到集合中
 8         if (root->left == NULL && root->right == NULL) {
 9             res.push_back(to_string(root->val) + "");
10             return res;
11         }
12         //遍历左子节点的路径
13         for (string path : binaryTreePaths(root->left)) {
14             res.push_back(to_string(root->val) + "->" + path);
15         }
16         //遍历右子节点的路径
17         for (string path : binaryTreePaths(root->right)) {
18             res.push_back(to_string(root->val) + "->" + path);
19         }
20         return res;
21     }
22 };

View Code

5.左叶子之和

5.1.问题描述

给定二叉树的根节点 root ，返回所有左叶子之和。

输入: root = [3,9,20,null,null,15,7] ；输出: 24 ；解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24
链接：https://leetcode.cn/problems/sum-of-left-leaves

5.2.要点

只统计左叶子

5.3.代码实例

递归

 1 class Solution {
 2 public:
 3     int leftSum=0;
 4     int sumOfLeftLeaves(TreeNode* root) {
 5         if(root==NULL){
 6             return 0;
 7         }
 8 
 9         if(root->left){
10             if(root->left->left==NULL&&root->left->right==NULL){
11                 leftSum+=root->left->val;
12             }
13             else{
14                 sumOfLeftLeaves(root->left);
15             }
16         }
17 
18         if(root->right){
19             sumOfLeftLeaves(root->right);
20         }
21         
22         return leftSum;
23     }
24 };

View Code

6.找树左下角的值

6.1.问题描述

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层最左边 节点的值。

假设二叉树中至少有一个节点。

输入: root = [2,1,3]；输出: 1

链接：https://leetcode.cn/problems/find-bottom-left-tree-value/

6.2.要点

层序遍历时保存当前层的第一个元素

6.3.代码实例

迭代、层序遍历

 1 class Solution {
 2 public:
 3     int findBottomLeftValue(TreeNode* root) {        
 4         int ret=0;        
 5         queue<TreeNode*> que;
 6         if (root != NULL) que.push(root);
 7         while (!que.empty()) {
 8             int size = que.size();
 9             // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
10             for (int i = 0; i < size; i++) {
11                 if(i==0){
12                     ret=que.front()->val;
13                 }
14                 TreeNode* node = que.front();
15                 que.pop();
16                 
17                 if (node->left) que.push(node->left);
18                 if (node->right) que.push(node->right);
19             }
20         }
21         return ret;
22     }
23 };

View Code

7.路径之和是否存在

7.1.问题描述

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在根节点到叶子节点的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。
叶子节点是指没有子节点的节点。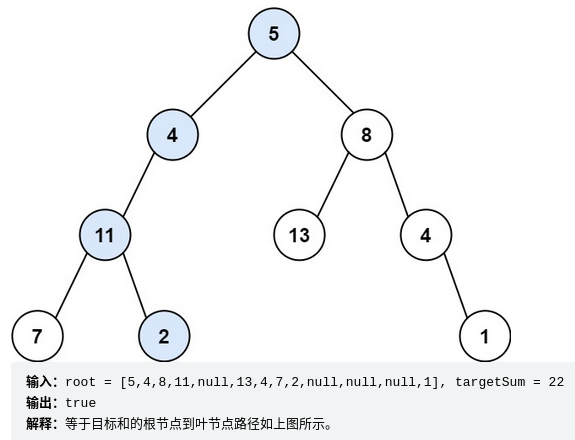

链接：https://leetcode.cn/problems/path-sum

7.2.要点

递归+回溯，找到了匹配路径则立即返回

7.3.代码实例

递归+回溯

 1 class Solution {
 2 public:
 3     bool hasPathSum(TreeNode* root, int targetSum) {
 4         //中止条件
 5         if(root==NULL){
 6             return false;
 7         }
 8 
 9         //本层逻辑
10         if(root->left==NULL&&root->right==NULL){
11             return root->val==targetSum;
12         }
13 
14         bool isExist=false;
15         isExist=hasPathSum(root->left,targetSum-root->val);
16         if(isExist){
17             return true;
18         }
19         isExist=hasPathSum(root->right,targetSum-root->val);
20         if(isExist){
21             return true;
22         }
23 
24         return false;
25     }
26 };

View Code

8.路径之和是否存在2

8.1.问题描述

给你二叉树的根节点 root 和一个整数目标和 targetSum ，找出所有从根节点到叶子节点路径总和等于给定目标和的路径。
叶子节点是指没有子节点的节点。
链接：https://leetcode.cn/problems/path-sum-ii

8.2.要点

路径搜索很正常，关键是要缓存中间路径以便回溯。

注意解法中使用数组进行回溯的方式。

8.3.代码实例

递归+缓存

 1 /**
 2  * Definition for a binary tree node.
 3  * struct TreeNode {
 4  *     int val;
 5  *     TreeNode *left;
 6  *     TreeNode *right;
 7  *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 8  *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 9  *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
10  * };
11  */
12 class Solution {
13 private:
14     vector<vector<int>> result;
15     vector<int> path;
16     // 递归函数不需要返回值，因为我们要遍历整个树
17     void traversal(TreeNode* cur, int count) {
18         // 遇到了叶子节点
19         if (cur->left==NULL && cur->right==NULL) {
20             if(count==0){//找到了和为sum的路径
21                 result.push_back(path);
22             }
23             return;
24         }
25 
26         if (cur->left) { // 左 （空节点不遍历）
27             path.push_back(cur->left->val);
28             count -= cur->left->val;
29             traversal(cur->left, count);    // 递归
30             count += cur->left->val;        // 回溯
31             path.pop_back();                // 回溯
32         }
33         if (cur->right) { // 右 （空节点不遍历）
34             path.push_back(cur->right->val);
35             count -= cur->right->val;
36             traversal(cur->right, count);   // 递归
37             count += cur->right->val;       // 回溯
38             path.pop_back();                // 回溯
39         }
40         return ;
41     }
42 
43 public:
44     vector<vector<int>> pathSum(TreeNode* root, int sum) {
45         result.clear();
46         path.clear();
47         if (root == NULL) return result;
48         path.push_back(root->val); // 把根节点放进路径
49         traversal(root, sum - root->val);
50         return result;
51     }
52 };

View Code

9.总结

9.1.要点

二叉树的属性，主要包括：

（1）左右结构；

（2）层次结构；

（3）前、中、后遍历方式与递归、迭代的结合策略；

xxx.问题

xxx.1.问题描述

111

xxx.2.要点

222

xxx.3.代码实例

333

posted @ 2022-12-17 20:47 啊原来是这样呀阅读(10) 评论(0) 编辑收藏举报

刷新页面返回顶部

OhOfCourse

【LeetCode】10.二叉树系列——属性

总目录：

1.判定对称二叉树

1.1.问题描述

1.2.要点

1.3.代码实例

2.完全二叉树的节点个数

2.1.问题描述

2.2.要点

2.3.代码实例

3.判定平衡二叉树

3.1.问题描述

3.2.要点

3.3.代码实例

4.二叉树的所有路径

4.1.问题描述

4.2.要点

4.3.代码实例

5.左叶子之和

5.1.问题描述

5.2.要点

5.3.代码实例

6.找树左下角的值

6.1.问题描述

6.2.要点

6.3.代码实例

7.路径之和是否存在

7.1.问题描述

7.2.要点

7.3.代码实例

8.路径之和是否存在2

8.1.问题描述

8.2.要点

8.3.代码实例

9.总结

9.1.要点

xxx.问题

xxx.1.问题描述

xxx.2.要点

xxx.3.代码实例

公告