【LeetCode】9.二叉树系列——遍历

总目录：

LeetCode系列导航目录

 

0.理论基础

0.1如何遍历

 

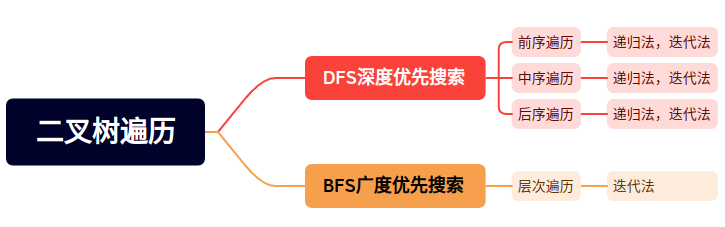
0.2.如何写递归

三板斧

（1）确定入参和返回值，如果需要搜索全部范围则不需要返回值，如果搜到目标值就需立即返回的话就必须返回值；

（2）确定终止条件；

（3）确定本层逻辑，包括数据处理和调用自身函数实现递归；

0.3.递归版DFS

以前序遍历为例：

    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }

0.4.迭代版DFS

前、中、后序的结构不太一样，需要具体顺序具体分析。尤其是中序遍历。

具体代码见下方。

0.5.迭代版BFS

层序遍历，一层一层地从左到右处理节点。

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

0.6.递归版BFS

输入层号，进行递归

# 递归法
class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};

 

1.二叉树递归版前中后序遍历

1.1.问题描述

分别用递归实现二叉树的前中后序遍历

链接：

https://leetcode.cn/problems/binary-tree-preorder-traversal/

https://leetcode.cn/problems/binary-tree-inorder-traversal/

https://leetcode.cn/problems/binary-tree-postorder-traversal/

1.2.要点

递归三板斧、弄清楚根节点数据在哪个顺位被处理

1.3.代码实例

前

class Solution {
public:
    void recurve(vector<int>& vec,const TreeNode* root){
        if(root==NULL){
            return;
        }
        
        vec.push_back(root->val);
        recurve(vec,root->left);
        recurve(vec,root->right);
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> vec;
        if(root==NULL){
            return vec;
        }
        recurve(vec,root);

        return vec;
    }
};

中

class Solution {
public:
    void recurve(vector<int>& vec,const TreeNode* root){
        if(root==NULL){
            return;
        }
                
        recurve(vec,root->left);
        vec.push_back(root->val);
        recurve(vec,root->right);
    }
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> vec;
        if(root==NULL){
            return vec;
        }
        recurve(vec,root);

        return vec;
    }
};

后

class Solution {
public:
    void recurve(vector<int>& vec,const TreeNode* root){
        if(root==NULL){
            return;
        }
                
        recurve(vec,root->left);        
        recurve(vec,root->right);
        vec.push_back(root->val);
    }
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> vec;
        if(root==NULL){
            return vec;
        }
        recurve(vec,root);

        return vec;
    }
};

 

2.二叉树迭代版前中后序遍历

2.1.问题描述

分别用迭代实现二叉树的前中后序遍历

链接：同上一题

2.2.要点

用迭代法来遍历树较为少用，关键还是其对栈的运用技巧，如何保存中间变量。

递归的本质就是将中间过程压栈弹栈，迭代时使用栈来实现。

前序迭代，访问顺序和处理顺序一致：

（1）while迭代判断栈是否为空；

（2）取栈顶元素，处理它的数据；

（3）先入栈其右子节点，如果有；再入栈其左子节点，如果有。

中序迭代，访问顺序和处理顺序不一致：记住固定套路。

后序迭代，前序迭代是中左右，后序迭代是左右中。将前序迭代改一下变成中右左，然后将结果翻转一下即可。

2.3.代码实例

前

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

中

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;

        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        
        return result;
    }
};

后

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> vec;
        if(root==NULL){
            return vec;
        }

        stack<TreeNode*> nodeSt;
        nodeSt.push(root);
        TreeNode* cur=NULL;
        while(!nodeSt.empty()){
            cur=nodeSt.top();
            nodeSt.pop();

            vec.push_back(cur->val);
            if(cur->left!=NULL){nodeSt.push(cur->left);}
            if(cur->right!=NULL){nodeSt.push(cur->right);}
        }
        reverse(vec.begin(),vec.end());
        return vec;
    }
};

 

3.二叉树的层序遍历,从上到下/从下到上

3.1.问题描述

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

链接：https://leetcode.cn/problems/binary-tree-level-order-traversal/

链接：https://leetcode.cn/problems/binary-tree-level-order-traversal-ii/

3.2.要点

层序的不同最后再处理

1迭代法

2递归法

3.3.代码实例

迭代法

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

递归版

class Solution {
public:
    void recurve(vector<vector<int>>& vec,TreeNode* root,int levelId){
        if(root==NULL){
            return;
        }        
        while(vec.size()<=levelId){
            vec.push_back(vector<int>());
        }
        vec[levelId].push_back(root->val);
        recurve(vec,root->left,levelId+1);
        recurve(vec,root->right,levelId+1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> vec;
        int levelId=0;
        recurve(vec,root,0);
        return vec;
    }
};

 

4.二叉树的右视图

4.1.问题描述

给定一个二叉树的 根节点 root，想象自己站在它的右侧，按照从顶部到底部的顺序，返回从右侧所能看到的节点值。

 

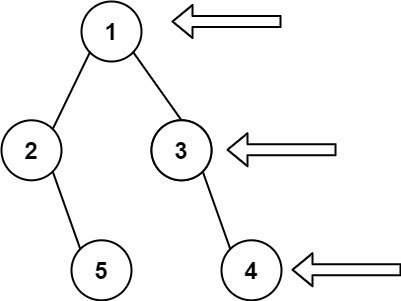
 输入: [1,2,3,null,5,null,4] 输出: [1,3,4]

链接：https://leetcode.cn/problems/binary-tree-right-side-view/

4.2.要点

迭代版层序遍历，每层只取最后一个

4.3.代码实例

迭代版层序遍历

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<int> result;
        while (!que.empty()) {
            int size = que.size();
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                if(i==(size-1)){
                    result.push_back(node->val);
                }                
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }
};

 

5.二叉树的各层平均值

5.1.问题描述

给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10-5 以内的答案可以被接受。

链接：https://leetcode.cn/problems/average-of-levels-in-binary-tree/

5.2.要点

求各层中节点之和后取平均值

1迭代式层序遍历

5.3.代码实例

迭代式层序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<double> averageOfLevels(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);

        vector<double> result;
        double sum=0;
        while (!que.empty()) {
            int size = que.size();
            sum=0;

            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();

                sum+=1.0*node->val;

                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }

            result.push_back(sum/size);
        }
        return result;
    }
};

 

6.N叉树的层序遍历

6.1.问题描述

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

 

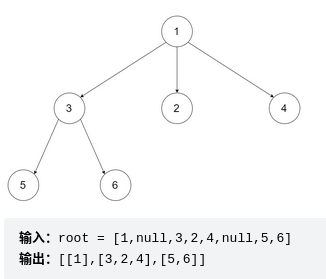
 链接：https://leetcode.cn/problems/n-ary-tree-level-order-traversal/

6.2.要点

处理每个节点的child集合，而不是左右子节点

1迭代式层序遍历

6.3.代码实例

迭代式层序遍历

/*
// Definition for a Node.
class Node {
public:
    int val;
    vector<Node*> children;

    Node() {}

    Node(int _val) {
        val = _val;
    }

    Node(int _val, vector<Node*> _children) {
        val = _val;
        children = _children;
    }
};
*/

class Solution {
public:
    vector<vector<int>> levelOrder(Node* root) {
        queue<Node*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                vec.push_back(node->val);

                for(Node*& child:node->children){
                    if (child) que.push(child);
                }
            }
            result.push_back(vec);
        }
        return result;
    }
};

 

7.在二叉树的每层找出最大值

7.1.问题描述

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

链接：https://leetcode.cn/problems/find-largest-value-in-each-tree-row/

7.2.要点

1迭代式层序遍历

7.3.代码实例

略

 

8.填充每个节点的右侧节点

8.1.问题描述

给定一个 完美二叉树 ，其所有叶子节点都在同一层，每个父节点都有两个子节点。二叉树定义如下：

struct Node {
  int val;
  Node *left;
  Node *right;
  Node *next;
}

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。
初始状态下，所有 next 指针都被设置为 NULL。

 

 
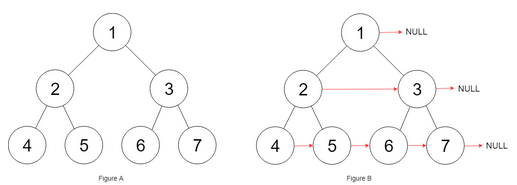
链接：https://leetcode.cn/problems/populating-next-right-pointers-in-each-node

链接：https://leetcode.cn/problems/populating-next-right-pointers-in-each-node-ii/

8.2.要点

1迭代式层序遍历

8.3.代码实例

略

 

9.二叉树的最大深度

9.1.问题描述

给定一个二叉树，找出其最大深度。

二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。

说明: 叶子节点是指没有子节点的节点。

示例：
给定二叉树 [3,9,20,null,null,15,7]，
    3
   / \
  9  20
    /  \
   15   7
返回它的最大深度 3 。
链接：https://leetcode.cn/problems/maximum-depth-of-binary-tree

9.2.要点

1迭代式层序遍历,levelCnt++

9.3.代码实例

略

 

10.二叉树的最小深度

10.1.问题描述

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

 

 链接：https://leetcode.cn/problems/minimum-depth-of-binary-tree/

10.2.要点

遇到叶子节点就要比较一下深度最小值

1迭代式层序遍历,levelCnt++，与levelMin作比较

10.3.代码实例

略

 

11.翻转二叉树

11.1.问题描述

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

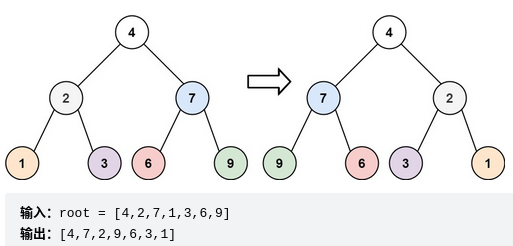
链接：https://leetcode.cn/problems/invert-binary-tree/

11.2.要点

递归交换左右节点，不可使用中序遍历，可以使用前序和后序遍历。

11.3.代码实例

递归

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root==NULL){
            return NULL;
        }

        TreeNode* tmp=root->left;
        root->left=root->right;
        root->right=tmp;

        invertTree(root->left);
        invertTree(root->right);

        return root;
    }
};

 

12.遍历总结

12.1.遍历方式

策略上可以分为深度优先、广度优先，
具体实现上可以分为递归和迭代，迭代一般借助队列或栈。
深度优先的迭代实现方式较为麻烦，而且前、中、后的实现策略不一样，这一块需要特别练习。

 12.2实现

递归、栈迭代、队列迭代并不对立，都有各自的实现逻辑，具体实现例子可以参考

https://github.com/hitwzy/leetcode-master/blob/master/problems/0101.%E5%AF%B9%E7%A7%B0%E4%BA%8C%E5%8F%89%E6%A0%91.md

 

xxx.问题

xxx.1.问题描述

111

xxx.2.要点

222

xxx.3.代码实例

333