【剑指offer】77.孩子们的游戏(圆圈中最后剩下的数)

总目录：

算法之旅导航目录

 

1.问题描述

 每年六一儿童节，牛客都会准备一些小礼物和小游戏去看望孤儿院的孩子们。其中，有个游戏是这样的：首先，让 n 个小朋友们围成一个大圈，小朋友们的编号是0~n-1。然后，随机指定一个数 m ，让编号为0的小朋友开始报数。每次喊到 m-1 的那个小朋友要出列唱首歌，然后可以在礼品箱中任意的挑选礼物，并且不再回到圈中，从他的下一个小朋友开始，继续0... m-1报数....这样下去....直到剩下最后一个小朋友，可以不用表演，并且拿到牛客礼品，请你试着想下，哪个小朋友会得到这份礼品呢？

 

数据范围：1≤n≤5000，1≤m≤10000

要求：空间复杂度 O(1)，时间复杂度 O(n)

 

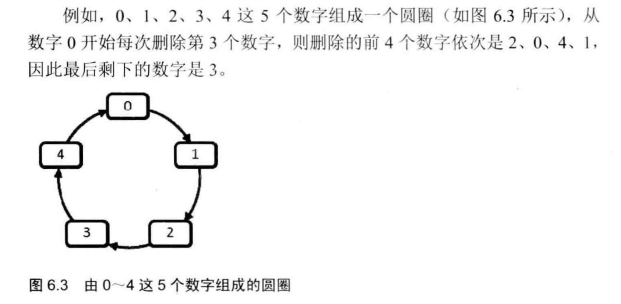
2.问题分析

 数学表达为环形结构，每轮迭代出队1个，直到剩下一个

1队列+迭代

直观来看，很明显使用队列可以方便地实现出队和重新入队，中间的人需要重新入队，排到的人出队后不再入队，直到队列中仅剩1人

 

2约瑟夫环

这类问题早有明确的数学研究，即约瑟夫环问题。属于动态规划问题，递推公式为f(N,M)=(f(N−1,M)+M)%N，在理解后直接套用即可。计算过程非常迅速，这就是算法的威力。

原理讲解 这个例子中的序号演算是从1开始的较为混乱，但推导过程没有问题可以辅助理解。

模拟过程如下：

有11个人分别为0~10，

（1）第一轮2出队，

（2）第二轮5出队，

。。。

（n-1）最后一轮，只剩7为所求值。

出队过程可以表述如下：

 

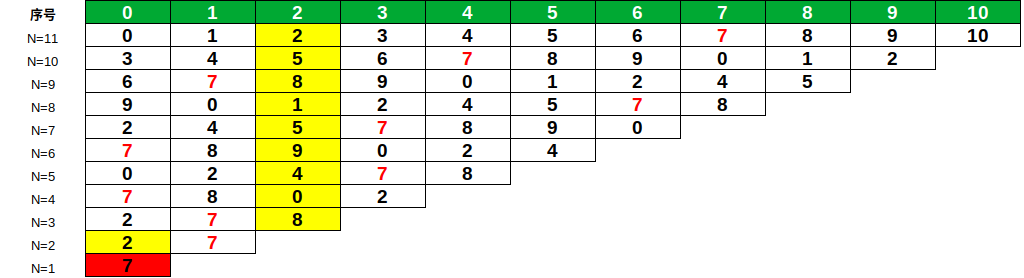
 将上面表格的每一行看成数组，可以看到最终胜利者在每一轮的下标位置（下标位置由绿色行来确定），而黄色即为在该轮出队的元素。

套用公式来验证：

（1）f(1,3)：只有1个人了，那个人就是获胜者，他的下标位置是0；

（2）f(2,3)=(f(1,3)+3)%2=3%2=1：在有2个人的时候，胜利者的下标位置为1；

（3）f(3,3)=(f(2,3)+3)%3=4%3=1：在有3个人的时候，胜利者的下标位置为1；

（4）f(4,3)=(f(3,3)+3)%4=4%4=0：在有4个人的时候，胜利者的下标位置为0；

。。。

（目标）f(11,3)=7；

 公式的推导过程：

问题1： 假设我们已经知道11个人时，胜利者的下标位置为7。那下一轮10个人时，胜利者的下标位置为多少？
答： 其实吧，第一轮删掉编号为2的人后，之后的人都往前面移动了3位，胜利者也往前移动了3位，所以他的下标位置由7变成4。

问题2： 假设我们已经知道10个人时，胜利者的下标位置为4。那下一轮11个人时，胜利者的下标位置为多少？
答： 这可以看错是上一个问题的逆过程，大家都往后移动3位，所以f ( 11 , 3 ) = f ( 10 , 3 ) + 3 。不过有可能数组会越界，所以最后模上当前人数的个数，f ( 11 , 3 ) = （ f ( 10 , 3 ) + 3 ） % 11

问题3： 现在改为人数改为N，报到M时，把那个人出队，那么数组是怎么移动的？
答： 每出队一个人，下一个人成为头，相当于把数组向前移动M位。若已知N-1个人时，胜利者的下标位置位f(N−1,M)，则N个人的时候，就是往后移动M位，(因为有可能数组越界，超过的部分会被接到头上，所以还要模N)，既f(N,M)=(f(N−1,M)+M)%N

3.代码实例

队列+迭代

class Solution {
  public:
    int LastRemaining_Solution(int n, int m) {
        queue<int> children;
        for (int i = 0; i < n; i++) {
            children.push(i);
        }

        int ret = 0;
        int tempChild = 0;
        while (children.size() > 1) {
            //数m个
            for (int j = 0; j < m; j++) {
                tempChild = children.front();
                children.pop();

                //中间的重新入队
                if (j != (m - 1)) {
                    children.push(tempChild);
                }
            }
        }

        return children.front();
    }
};

 约瑟夫环

class Solution {
  public:
    int LastRemaining_Solution(int n, int m) {
        int p = 0;
        for (int i = 2; i <= n; i++) {
            p = (p + m) % i;
        }
        return p;
    }
};