【剑指offer】28.在二叉树中找到两个节点的最近公共祖先

总目录：

算法之旅导航目录

 

1.问题描述 

给定一棵二叉树(保证非空)以及这棵树上的两个节点对应的val值 o1 和 o2，请找到 o1 和 o2 的最近公共祖先节点。

数据范围：树上节点数满足 1≤n≤10^5 , 节点值val满足区间 [0,n)

要求：时间复杂度 O(n)

注：本题保证二叉树中每个节点的val值均不相同。

如当输入{3,5,1,6,2,0,8,#,#,7,4},5,1时，二叉树{3,5,1,6,2,0,8,#,#,7,4}如下图所示：

 

 

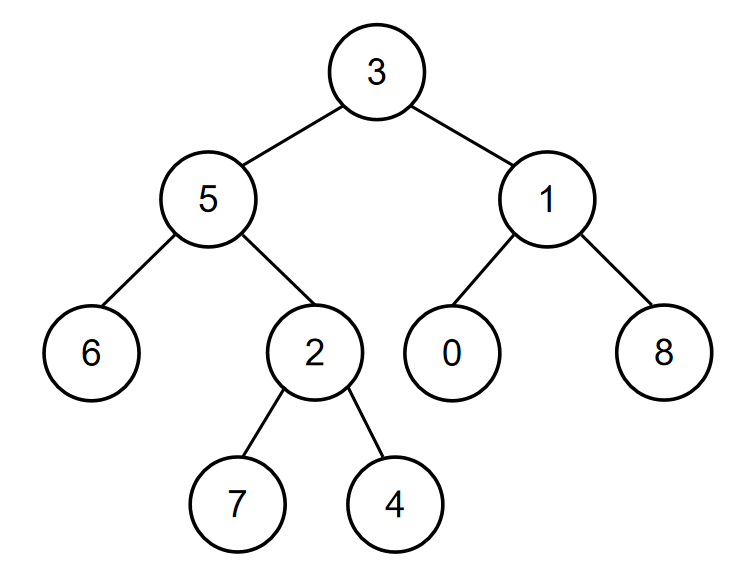
所以节点值为5和节点值为1的节点的最近公共祖先节点的节点值为3，所以对应的输出为3。

节点本身可以视为自己的祖先

 

2.问题分析

 1递归，两次DFS获得两个节点的路径，然后对比两个路径获得最后一个共同点，在数据处理上不太安全、优雅

2层序遍历

　　以下高亮的部分需要熟悉常用集合的使用，如map、set、queue它们对的添加、删除和查找。

1. 通过bfs，层序遍历这棵树，记录每个节点的父节点，因为o1和o2的孩子与本题无关，所以只需遍历到o1和o2就可以了。
2. 从o1开始，跑出o1到root的路径。
3. 从o2开始，往o2的父亲逆向遍历找，同时在o1到root的路径中查找这个点，如果没有则该点即为答案
4. 如果走到root也没找到，说明root是答案。

3.代码实例

最拉跨的递归

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 * };
 */
class Solution {
  public:
    /**
     *
     * @param root TreeNode类
     * @param o1 int整型
     * @param o2 int整型
     * @return int整型
     */
    bool findNodePath(TreeNode* root, int tgtVal, vector<TreeNode*>& path) {
        //中止条件
        if (!root) {
            return false;
        }

        //先压入
        path.push_back(root);

        if (root->val == tgtVal) {            
            return true;
        }
        if (findNodePath(root->left, tgtVal, path) ) {
            return true;
        }
        if (findNodePath(root->right, tgtVal, path) ) {
            return true;
        }

        path.pop_back(); //不在这条路径，去除节点

        return false;
    }
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        vector<TreeNode*> path1, path2;
        findNodePath(root, o1, path1);
        findNodePath(root, o2, path2);

        auto size1 = path1.size();
        auto size2 = path2.size();
        for (int i = 0; i < size1 && i < size2;) {
            if (path1[i] != path2[i]) {
                return path1[i - 1]->val;
            }

            i++;
            if (i >= size1 || i >= size2) {
                return path1[i - 1]->val;
            }
        }

        return -1;
    }
};

层序遍历

class Solution {
  public:
    int lowestCommonAncestor(TreeNode* root, int o1, int o2) {
        //记录遍历到的每个节点的父节点。
        unordered_map<int, int> parent;
        queue<TreeNode*> queue;
        parent[root->val] = INT_MIN;
        queue.push(root);
        //直到两个节点都找到为止。
        while (parent.find(o1) == parent.end() || parent.find(o2) == parent.end()) {
            //队列是一边进一边出，这里是出队，
            TreeNode* node = queue.front();
            queue.pop();
            if (node->left != NULL) {
                //左子节点不为空，记录下他的父节点
                parent[node->left->val] = node->val;
                //左子节点不为空，把它加入到队列中
                queue.push(node->left);
            }
            //右节点同上
            if (node->right != NULL) {
                parent[node->right->val] = node->val;
                queue.push(node->right);
            }
        }
        set<int> ancestors;
        //记录下o1和他的祖先节点，从o1节点开始一直到根节点。
        while (parent.find(o1) != parent.end()) {
            ancestors.insert(o1);
            o1 = parent[o1];
        }
        //查看o1和他的祖先节点是否包含o2节点，如果不包含再看是否包含o2的父节点……
        while (ancestors.find(o2) == ancestors.end())
            o2 = parent[o2];
        return o2;
    }
};