【剑指offer】20.二叉搜索树的第k个节点

总目录：

算法之旅导航目录

 

1.问题描述

给定一棵结点数为n 二叉搜索树，请找出其中的第 k 小的TreeNode结点值。

1.返回第k小的节点值即可

2.不能查找的情况，如二叉树为空，则返回-1，或者k大于n等等，也返回-1

3.保证n个节点的值不一样

数据范围： 0≤n≤1000，0≤k≤1000，树上每个结点的值满足0≤val≤1000
进阶：空间复杂度 O(n)，时间复杂度 O(n)

如输入{5,3,7,2,4,6,8},3时，二叉树{5,3,7,2,4,6,8}如下图所示：

 

 

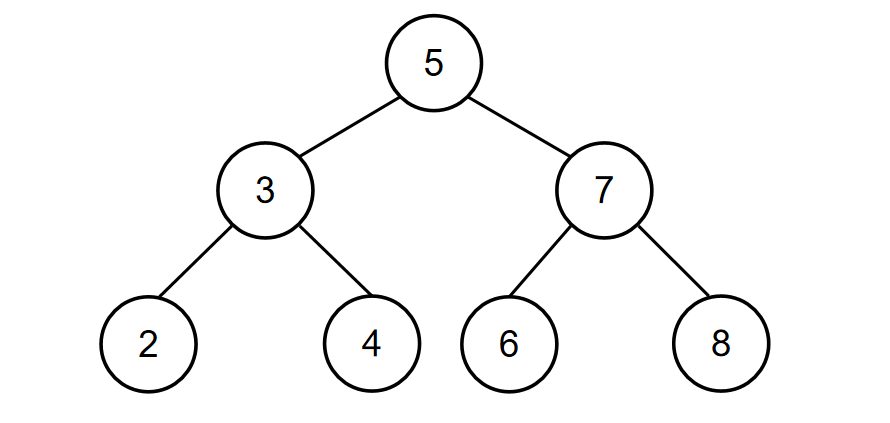
 该二叉树所有节点按结点值升序排列后可得[2,3,4,5,6,7,8]，所以第3个结点的结点值为4，故返回对应结点值为4的结点即可。

 

2.问题分析

  1递归，压栈拉来储值，因为是有序的搜索树，必须使用中序搜索

2粗暴迭代，逻辑较为复杂，但这种中序迭代方式值得学习，同样也必须是中序搜索

3.代码实例

递归

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 *  TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 * };
 */
class Solution {
  public:
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     *
     * @param proot TreeNode类
     * @param k int整型
     * @return int整型
     */
    stack<int> sp;
    int searchRet = -1;
    int recurve(TreeNode* root, int k) {
        //中止条件
        if (!root) {
            return -1;
        }

        //递归调用,中序搜索
        searchRet = recurve(root->left, k);
        if (searchRet >= 0) {
            return searchRet;
        }

        //本层逻辑
        sp.push(root->val);
        if (sp.size() == k) {
            return sp.top();
        }

        //递归调用
        searchRet = recurve(root->right, k);
        if (searchRet >= 0) {
            return searchRet;
        }

        return searchRet;
    }

    int KthNode(TreeNode* proot, int k) {
        if (k <= 0) {
            return -1;
        }
        return recurve(proot, k);
    }
};

 粗暴迭代

class Solution {
public:
    int KthNode(TreeNode* proot, int k) {
        if(proot == NULL)
            return -1;
        //记录遍历了多少个数
        int count = 0;  
        TreeNode* p = NULL;
        //用栈辅助建立中序
        stack<TreeNode*> s;   
        while(!s.empty() || proot != NULL){
            while (proot != NULL) {
                s.push(proot);
                //中序遍历每棵子树从最左开始
                proot = proot->left;   
            }
            p = s.top();
            s.pop();
            count++;
            //第k个直接返回
            if(count == k)
                return p->val;
            proot = p->right;
        }
        //没有找到
        return -1;
    }
};