【剑指offer】14.二叉树中和为某一值的路径(一)

总目录：

算法之旅导航目录

 

1.问题描述

给定一个二叉树root和一个值 sum ，判断是否有从根节点到叶子节点的节点值之和等于 sum 的路径。

1.该题路径定义为从树的根结点开始往下一直到叶子结点所经过的结点

2.叶子节点是指没有子节点的节点

3.路径只能从父节点到子节点，不能从子节点到父节点

4.总节点数目为n

例如：
给出如下的二叉树， sum=22 sum=22，

 

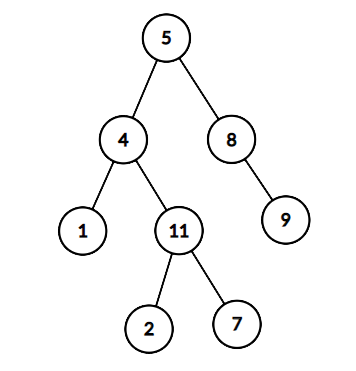
返回true，因为存在一条路径 5→4→11→25→4→11→2的节点值之和为 22

数据范围：

1.树上的节点数满足 0≤n≤10000

2.每 个节点的值都满足 ∣val∣≤1000

要求：空间复杂度 O(n)，时间复杂度 O(n)

进阶：空间复杂度 O(树的高度)，时间复杂度 O(n)

 

2.问题分析

1递归法，递归到叶节点为止，检查一路下来值和

2用栈，深度搜索，栈顶是从根节点一路加下来的和，到了某个叶子节点处如果不符合要求则返回false，到了非叶子节点处要将累加到本节点的和分别加上子节点的值并压栈。

3.代码实例

递归

/**
 * struct TreeNode {
 *  int val;
 *  struct TreeNode *left;
 *  struct TreeNode *right;
 * };
 */

class Solution {
  public:
    /**
     *
     * @param root TreeNode类
     * @param sum int整型
     * @return bool布尔型
     */
    bool AddToEndRecurve(TreeNode* root, const int tgtSum, int curSum) {
        //中止条件，到叶子节点时才判断
        if (!root) {
            return false;
        }
        curSum += root->val;
        if (root->left == NULL && root->right == NULL) {
            return curSum == tgtSum;
        }

        //递归调用
        auto isLeft = AddToEndRecurve(root->left, tgtSum, curSum);
        auto isRight = AddToEndRecurve(root->right, tgtSum, curSum);
        return isLeft || isRight;
    }
    
    bool hasPathSum(TreeNode* root, int sum) {
        int curSum = 0;
        return AddToEndRecurve(root, sum, curSum);
    }
};

 栈，深度优先搜索

class Solution {
public:
    bool hasPathSum(TreeNode* root, int sum) {
        //空节点找不到路径
        if(root == NULL) 
            return false;
        //栈辅助深度优先遍历，并记录到相应节点的路径和
        stack<pair<TreeNode*, int> > s; 
        //根节点入栈
        s.push({root, root->val}); 
        while(!s.empty()){
            auto temp = s.top();
            s.pop();
            //叶子节点且路径和等于sum
            if(temp.first->left == NULL && temp.first->right == NULL && temp.second == sum)
                return true;
            //左节点入栈
            if(temp.first->left != NULL) 
                s.push({temp.first->left, temp.second + temp.first->left->val});
            //右节点入栈
            if(temp.first->right != NULL) 
                s.push({temp.first->right, temp.second + temp.first->right->val});
        }
        return false;
    }
};