【剑指offer】11.二叉树的深度

总目录：

算法之旅导航目录

 

1.问题描述

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度，根节点的深度视为 1 。

数据范围：节点的数量满足 0≤n≤100，节点上的值满足 0≤val≤100

进阶：空间复杂度 O(1) ，时间复杂度 O(n)

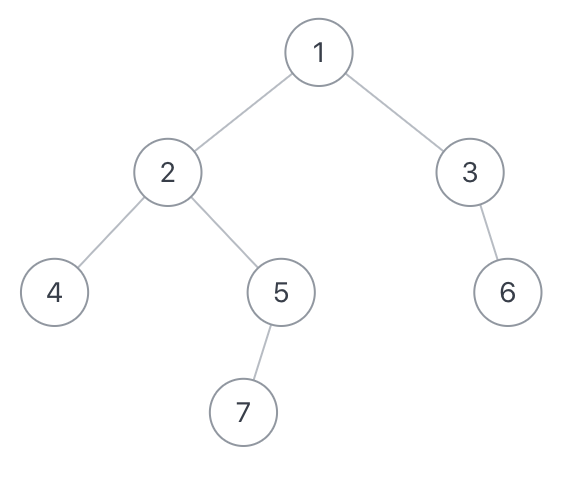
假如输入的用例为{1,2,3,4,5,#,6,#,#,7}，那么如下图:

 

2.问题分析

这道题的意义其实比较深远，可以引出深度搜索DFS(Deep first search)和广度搜索BFS(Broad first search)两个概念。

1用递归，最方便

2用辅助队列，逐层遍历，将当前层的节点入队，然后迭代队列长度，边迭代边出队，同时将出队节点的子节点入队。每走一层计数器+1，直至队列中无节点

3.代码实例

递归

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
  public:
    int TreeDepth(TreeNode* pRoot) {
        //中止条件
        if (!pRoot) {
            return 0;
        }

        //递归调用
        int leftDep = TreeDepth(pRoot->left);
        int rightDep = TreeDepth(pRoot->right);

        //本层逻辑
        return leftDep > rightDep ? (leftDep + 1) : (rightDep + 1);
    }
};

队列

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
  public:
    int TreeDepth(TreeNode* pRoot) {
        //空树
        if (!pRoot) {
            return 0;
        }

        //初始化队列
        queue<TreeNode*> q;
        q.push(pRoot);

        //初始化计数器
        int nodeCount = 0;
        int depth = 0;

        //逐层迭代
        while (!q.empty()) {
            //遍历当前层的所有节点
            nodeCount = q.size();
            for (int i = 0; i < nodeCount; i++) {
                auto* pNode = q.front();
                q.pop();

                if(pNode->left) q.push(pNode->left);
                if(pNode->right) q.push(pNode->right);
            }

            //本层结束，计数器++
            depth++;
        }
        return depth;
    }
};