最短路算法大全(Bellman-Ford &Spfa)

Bellman-Ford算法

1、基于松弛操作的单源最短路算法,针对于有向图、
2、e[u]存u点的出边的邻点和边权，d[u]存u点到原点的距离
3、初始化，d[s] = 0,d[其他点]=INF （源点到本身的距离初始化为0到其他点的距离都初始化为无穷）
4、执行多轮操作。每轮操作都对所有边尝试一次松弛操作
5、当一轮循环中没有成功的松弛操作后，算法就停止
算法模板：
对于一组数据n个点，m条边 s是要找的原点
接下来m条内容，a,b是两个点,c是边的权值

struct edge{int v,int w;};
vector<edge> e(N);
int d[N];
 
bool bellmanford(int s){
    memset(d,INF,sizeof d);
    d[s] = 0;
    bool flag;//是否松弛
    for(int i=1; i<=n; i++){//n轮
        flag = false;
        for(int u = 1; u<=n; u++){//对每个点枚举出边
            if(d[u] == INF)continue;
            for(auto ed:e[u]){//枚举每个u的出边
                int v = ed.v,w = ed.w;//v来存出边的终点,w来存边权，这就是松弛操作的条件
                if(d[v] > d[u] + w){
                    d[v] = d[u] + w;
                    flag = true;
                }
            }
        }
        if(!flag)break;
    }
    return flag; //第n轮=true则有环
} 
 
int main()
{
    cin>>n>>m>>s;
    for(int i=0;i<m;i++)
    {
        cin>>a>>b>>c;
        e[a].push_back({b,c});
    }
}

整个过程模拟：

i指的是每一轮的循环,
i=1  u=1
     u=2
     u=3 d[1]=6 d[2]=1
     u=4
i=2  u=1 d[4]=9
     u=2 d[1]=2 d[4]=6
     u=3 
     u=4
i=3  u=1 d[4]=5
     u=2,3,4
i=4  u=1,2,3,4
 
     flag=false

Bellman-Ford算法可以正确的处理负边权

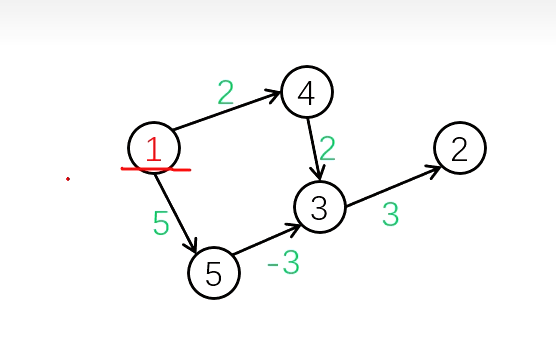
Bellman Ford 可以处理有负边的图

时间复杂度

没轮循环是O(m)的，如果最短路存在，一轮松弛操作会使最短路的边数至少执行+1，而最短路的边数最多为n-1最多执行n-1论松弛操作，故时间复杂度为O(nm)
如果第n轮循环时仍然存在能松弛的边，说明从s点出发，能够抵达一个负环，因此bellman-Ford算法还可以判断负环

Spfa（bellmanford的优化）

原理：只有本轮被更新的点，其出边才有可能引起下一轮的松弛操作，因此用队列来维护被更新的点的集合

vis[u]标记u点是否在队内，cnt[v]记录边数判断负环。

• 1.初始化，原点s入队,标记s在队内d[s] = 0,d[其他点] = +无穷
• 2.从队头弹出u点，标记u不在队内
• 3.枚举u的所有出边，执行松弛操作。记录s走到v的边数，并判断负环。如果v不在队内就把v压入队尾，并打上标记；
• 4.重复2,3步操作，直到队列为空

struct edge{int v,w;};
vector<edge> e[N];
int d[N],cnt[N],vis[N];
queue<int> q;
 
bool spfa(int s){
    memset(d,inf,szieof d);//初始化每个点的距离
    d[s]=0;//
    vis[s]=1;//原点标记他等于1等于true
    q.push(s);
    while(q.size()){
        int u=q.front();
        q.pop();
        vis[u]=0;//出队后就将其标记为false
        for(auto ed:e[u]){
            int v = ed.v,w=ed.w;
            if(d[v]>d[u]+w){
                d[v]=d[u]+w;//如果新的路径更短
                cnt[v]=cnt[u]+1;//记录从v点走到u点都经过了一条边
                if(cnt[v]>=n)return true;
                //v点被更新且不在队内，则入队
                if(!vis[v])q.push(v),vis[v]=1;
                //如果v不在队内就把v压入队尾，并打上标记
            }
        }
        
    }
    return false;
}