拓扑排序

拓扑排序

给定一张有向无环图，排出所有顶点的一个序列A满足:
对于图中的每条有向边（x,y）x在A中的出现都在y之前，则称A是改图的顶点的一个拓扑序。

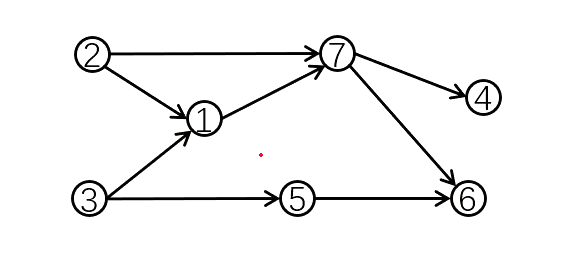
如图所示，{2 3 5 1 7 4 6},{3 2 1 5 7 6 4}都是合法的拓扑序。

用途：

可以判断有向图中是否有环，可以生成拓扑排序

Kahn算法实现拓扑排序

e[x]存点x的邻点，tp存拓朴序列，din[x]存点x的入度。

算法的核心：

用队列维护一个入度为0的节点的集合。

• 1.初始化，队列q压入所有入度为0的点的集合.(起始步)
• 2.每次从q中取出一个点x放入数组tp[]当中
• 3.然后将x的所有出边删除。若将边(x,y)删除后,y的入度变为0,则将y也压入q中；
• 4.不断重复2,3过程，直到队列q为空。
• 5.若tp[]中元素的个数等于n，则有拓扑序；否则，有环.

代码模板如下所示:

vector<int> e[N],tp;
int din[N];
 
bool topsort()
{
    queue<int>q;//维护入度为零的点
    for(int i=1;i<=n;i++)
    if(din[i]==0)q.push(i);
    while(q.size())//只要队不空,就从队头取出一个元素弹出
    {
        int x=q.front();
        q.pop();
        tp.push_back(x);//将取出的元素压入tp数组
        for(auto y:e[x])
        {
            if(--din[y]==0)q.push(y);//判断每次减一的时候入度有没有变为0
        }
    }
    return tp.size()==n;
}
int main()
{
    cin>>n>>m;
    for(int i=0;i<m;i++)
    {
        cin>>a>>b;
        e[a].push_back(b);//压入a的临点b
        din[b]++;//同时b的入度要加 1
    }
    if(!topsort())puts("-1");//有环无解
    else for(auto x:tp)printf("%d ",x);//迭代循环输出
    return 0;
}

DFS实现拓扑排序

e[x]存x的临点,tp存拓扑序列,c[x]存点的颜色
算法的核心是变色法,一路搜索一路给点进行变色,如果有拓扑排序,每个点的颜色都会从0 -> -1 ->1,经历3次变色

• 1.初始状态所有的状态都染色为0;
• 2.枚举每个点,进入x点,就把x染色为-1.然后,枚举x的儿子节点y,如果y的颜色为0,说明没碰过该点,进入y继续走
• 3.如果枚举完x的儿子,没发现环,则x染色为1,并把x压入tp数组
• 4.如果发现有个熊孩子的颜色为-1,说明回到了祖先节点,发现了环,则一路返回false,退出程序.

代码模板如下所示:

vector<int> e[N],tp;
int c[N];//染色数组
 
bool dfs(int x)
{
    c[x]=-1;
    for(int y:e[X])
    {
        if(c[y]<0)return 0;//有环
        
        else if(!c[y])
        if(!dfs(y))return 0;
    }
    c[x]=1;
    tp.push_back(x);
    return 1;
}
 
bool topsort()
{
    memset(C,0,sizeof(c));
    for(int x=1;x<=n;x++)
    {
        if(!c[x])
            if(!dfs(x))return 0;
    }
    reverse(tp.begin(),tp.end());
    return 1;
}

总结

• Kahn算法 队列维护,顺着拓扑收集点
• dfs算法,系统栈维护,逆着拓扑序收集点
• 时间复杂度:O(E+V)
• 不连通:不影响拓扑排序
• 求字典序的最小拓扑序,将Kahn算法中的队列替换为优先队列(小根堆)
  时间复杂度为O(E+VlogV)