数据结构与算法笔试面试题整理
给出的一些常见的数据结构与算法的笔试面试题,特整理如下,后期遇到新的再更新。
笔试面试题
常见时空复杂度有
- 常数级复杂度:O(1)
- 对数级复杂度:O(logN)
- 线性级复杂度:O(N)
- 线性对数级复杂度:O(NlogN)
- 平方级复杂度:O(N2)
冒泡排序算法(重点)
(1)算法流程
a.比较两个相邻的元素,如果第一个比第二个大,则交换两个元素的位置;
b.对每一对相邻的元素做同样的工作,从开始的第一对一致到结尾的最后一对,经过这一步,最后的元素将是最大值;
c.针对所有的元素重复以上步骤,除了最后一个;
d.持续对越来越少的元素重复以上步骤,直到没有元素需要交换为止;
(2)算法评价(N代表元素个数)
评价时间复杂度O(N^2),比较稳定的排序方法,对样本的有序性敏感
插入排序算法
(1)算法流程
a.从第一个元素起,该元素可以认为已经有序
b.从下一个元素起依次取出,让取出的元素依次与左边的有序数列进行比较
c.如果左边的元素大于取出的元素,则左边的元素右移
d.如果左边的元素小于等于取出的元素,则将取出的元素插入到左边元素的右边,或者左边不再有元素,则将取出的元素插入到最左边;
e.重复以上过程,直到处理完毕所有的元素为止
(2)算法评价
平均时间复杂度O(N^2),比较稳定的排序方法,对样本的有序性非常敏感,但是插入排序算法的赋值次数比冒泡少,因此一般情况下略优于冒泡排序
选择排序
(1)算法流程
a.从第一个元素起依次取出,并且假定取出的元素为最小值,使用min记录该元素的下标
b.使用min记录的元素和后续的元素依次进行比较,如果后续元素中有比min记录的元素还小的元素,则重新记录该元素的下标到min中,也就是后续记录变成了min记录的最小值
c.直到min记录的最小值和后续所有的元素比较完毕,交换min记录的最小值和最开始假定的元素之间的位置,此时最小值被移动到了最左边
d.重复以上过程,直到处理完毕所有元素
(2)算法评价
平均时间复杂度O(N^2),不稳定,对样本的有序性不敏感,虽然该算法比较的次数多,但是交换的次数少,因此一般情况下也是略优于冒泡排序
例如 30 20 30 50 40,用选择排序会更改两个30的前后顺序,所以不稳定
快速排序算法
(1)算法流程
a.从样本数列中选择中间元素作为基准值,单独保存起来;
b.重组样本数列,将所有小于基准值的元素放在基准值的左边,将所有大于基准值的元素放在基准值的右边,这个过程叫做分组
c.以递归的方式分别对小于基准值的分组和大于基准值的分组进行再次分组,直到处理完毕所有的元素为止
(2)算法评价
平均时间复杂度O(NlogN),不稳定,如果每次都能做到均匀分组,则排序速度最快
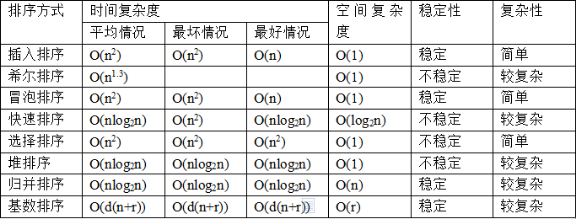
选择、冒泡、快速、插入、希尔、归并、堆排等。
1.快排:是冒泡排序的一种改进。
优点:快,数据移动少
缺点:稳定性不足
2.归并:分治法排序,稳定的排序算法,一般用于对总体无序,但局部有序的数列。
优点:效率高O(n),稳定
缺点:比较占用内存
希尔排序
void sort(int *array,int len){
int tmp,i,j,gap;
gap = len ;
do
{
gap = gap / 3 + 1;
for(i=0+gap;i<len;i++){
if(array[i]<array[i-gap]){
tmp = array[i];
for(j=i-gap;j>=0;j=j-gap)
if(array[j]>tmp)
array[j+gap]=array[j];
else
break;
array[j+gap]=tmp;
}
}
}while(gap > 1);
}
堆排序
static void heapAdjust(int * array,int start,int end);
void sort(int *array,int len){
int i,j;
for(i=len/2;i>=0;i--)
heapAdjust(array,i,len-1);
for(i=len-1;i>0;i--){
int tmp=array[i];
array[i]=array[0];
array[0]=tmp;
heapAdjust(array,0,i-1);
}
}
static void heapAdjust(int * array,int start,int end){
int i;
int tmp = array[start];
for(i=2*start+1;i<=end;i=2*i+1){
if(array[i]<array[i+1]&& i<end)
i++;
if(tmp > array[i])
break;
array[start]=array[i];
start = i;
}
array[start]=tmp;
}
插排、冒泡、快排
//编程实现各种排序算法
#include <stdio.h>
//实现冒泡排序算法
void bubble(int arr[],int len)
{
int i = 0,j = 0;
//使用外层循环来控制比较的轮数
for(i = 1; i < len; i++)
{
//使用内层循环控制针对当前轮比较的元素下标
int flag = 1;
for(j = 0; j < len-i; j++)
{
//如果第一个元素大于第二个元素,则交换
if(arr[j] > arr[j+1])
{
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
//表明有数据元素发生了交换
flag = 0;
}
}
//表示刚才的一轮扫描中没有发生交换
if(1 == flag)
{
// 省略剩余的轮数
break;
}
}
}
//实现插入排序算法
void insert(int arr[],int len)
{
int i = 0,j = 0;
//从第二个元素起,依次取出每个元素
for(i = 1; i < len; i++)
{
//使用临时变量记录取出的当前元素值
int temp = arr[i];
//使用取出的元素与左边的有序数列依次比较,如果左边的元素大,则左边元素右移;
for(j = i; arr[j-1] > temp && j >= 1; j--)
{
arr[j] = arr[j-1];
}
//直到左边元素不再大于取出元素时,插入取出元素
if(j != i)
{
arr[j] = temp;
}
}
}
//实现选择排序算法
void choose(int arr[],int len)
{
int i = 0,j = 0;
//从第一个元素起依次取出,使用min记录下标
for(i = 0; i < len-1; i++)
{
int min = i;
//使用取出的元素与后续元素依次比较,如果找到比min记录元素还小的元素,则重新记录下标
for(j = i+1; j < len; j++)
{
if(arr[j] < arr[min])
{
min = j;
}
}
//直到min记录的元素与后续所有元素比较完毕,交换min记录的元素和最开始取出的元素
if(min != i)
{
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
}
}
//实现快速排序
void quick(int arr[],int left,int right)
{
//1.寻找中间元素作为基准值,单独保存
int p = (left + right)/2;
int pivot = arr[p];
//2.分别使用左边元素和右边元素与基准值进行比较,将小于基准值的元素放在左边,将大于等于基准值的元素放在右边;
int i = 0,j = 0;
for(i = left,j = right; i < j; )
{
//如果左边元素存在并且小于基准值时
while(arr[i] < pivot && i < p)
{
i++;
}
//如果左边元素存在,但是大于等于基准值
if(i < p)
{
arr[p] = arr[i];
p = i;
}
//接下来处理右边的元素
while(pivot <= arr[j] && p < j)
{
j--;
}
if(p < j)
{
arr[p] = arr[j];
p = j;
}
}
//3.将基准值放在重合的位置上
arr[p] = pivot;
//4.分别对左边分组和右边分组重复以上过程,使用递归处理
if(p-left > 1)
{
quick(arr,left,p-1);
}
if(right-p > 1)
{
quick(arr,p+1,right);
}
}
int main(void)
{
int arr[9] = {20,5,30,10,15,6,25,12,28};
//使用排序算法进行排序
//bubble(arr,9);
//insert(arr,9);
//choose(arr,9);
quick(arr,0,8);
printf("排序后的结果是:");
int i = 0;
for(i = 0; i < 9; i++)
{
printf("%d ",arr[i]);
}
printf("\n");
return 0;
}
链表
//编程实现单链表的各种操作
#include <stdio.h>
#include <stdlib.h>
//定义节点的数据类型
typedef struct Node
{
int data;//记录数据元素本身
struct Node* next;//记录下一个节点的地址
}Node;
//定义单链表的数据类型
typedef struct
{
Node* head;//记录头节点的地址
Node* tail;//记录尾节点的地址
int cnt;//记录元素的个数
}List;
//判断链表是否为空 empty
int empty(List* pl);
//判断链表是否为满 full
int full(List* pl);
//计算链表中节点个数 size
int size(List* pl);
//向头节点位置插入新元素的功能 push_head
void push_head(List* pl,int data);
//遍历链表中的所有节点元素值 travel
void travel(List* pl);
//编写创建新节点的函数 create_node
Node* create_node(int data);
//向链表的末尾追加新元素
void push_tail(List* pl,int data);
//向链表中任意的下标位置插入新元素
void insert_data(List* pl,int pos,int data);
//实现获取头节点的元素值 get_head
int get_head(List* pl);
//实现获取尾节点的元素值 get_tail
int get_tail(List* pl);
//实现删除头节点的功能 pop_head
int pop_head(List* pl);
//删除尾节点的功能函数
int pop_tail(List* pl);
//删除指定下标位置的节点
int delete_data(List* pl,int pos);
//逆转链表中所有节点
void reverse_data(List* pl);
//实现逆转的递归函数
void reverse(Node* pn);
//逆序打印链表中的所有节点元素
void reverse_travel_data(List* pl);
//实现逆序打印的递归函数
void reverse_travel(Node* pn);
//清空链表中所有的节点
void clear(List* pl);
int main(void)
{
//单链表的创建以及初始化
List list;
list.head = NULL;
list.tail = NULL;
list.cnt = 0;
push_head(&list,11);
travel(&list);// 11
push_head(&list,22);
travel(&list);// 22 11
push_head(&list,33);
travel(&list);// 33 22 11
printf("链表中节点元素的个数是:%d\n",size(&list));// 3
printf("%s\n",empty(&list)?"链表已经空了":"链表不为空");// 链表不为空
printf("%s\n",full(&list)?"链表已经满了":"链表没有满"); // 链表没有满
printf("--------------------------\n");
push_tail(&list,44);
travel(&list);// 33 22 11 44
push_tail(&list,55);
travel(&list);// 33 22 11 44 55
printf("链表中节点元素的个数是:%d\n",size(&list)); // 5
printf("---------------------------\n");
insert_data(&list,-2,66);
travel(&list);//33 22 11 44 55 66
insert_data(&list,0,77);
travel(&list);//77 33 22 11 44 55 66
insert_data(&list,2,88);
travel(&list);//77 33 88 22 11 44 55 66
insert_data(&list,8,99);
travel(&list);//77 33 88 22 11 44 55 66 99
printf("链表中节点元素的个数是:%d\n",size(&list)); // 9
printf("--------------------------\n");
printf("头节点的元素值是:%d\n",get_head(&list));// 77
printf("尾节点的元素值是:%d\n",get_tail(&list));// 99
printf("删除的头节点元素是:%d\n",pop_head(&list));// 77
travel(&list);//33 88 22 11 44 55 66 99
printf("头节点的元素值是:%d\n",get_head(&list));// 33
printf("尾节点的元素值是:%d\n",get_tail(&list));// 99
printf("链表中节点元素的个数是:%d\n",size(&list));// 8
printf("--------------------------\n");
travel(&list);//33 88 22 11 44 55 66 99
printf("删除的尾节点是:%d\n",pop_tail(&list));// 99
printf("链表中节点元素的个数是:%d\n",size(&list));// 7
travel(&list);//33 88 22 11 44 55 66
printf("删除的尾节点是:%d\n",pop_tail(&list));// 66
printf("链表中节点元素的个数是:%d\n",size(&list));// 6
travel(&list);//33 88 22 11 44 55
printf("---------------------------\n");
travel(&list);//33 88 22 11 44 55
printf("删除的节点元素是:%d\n",delete_data(&list,-2)); // -1
travel(&list);//33 88 22 11 44 55
printf("删除的节点元素是:%d\n",delete_data(&list,0));// 33
travel(&list);// 88 22 11 44 55
printf("删除的节点元素是:%d\n",delete_data(&list,2));// 11
travel(&list);// 88 22 44 55
printf("删除的节点元素是:%d\n",delete_data(&list,3));// 55
travel(&list);// 88 22 44
printf("--------------------------\n");
reverse_data(&list);
travel(&list);// 44 22 88
printf("--------------------------\n");
printf("逆序打印的结果是:");
reverse_travel_data(&list);// 88 22 44
printf("正序打印的结果是:");
travel(&list);// 44 22 88
printf("-----------------------\n");
clear(&list);
travel(&list); // 啥也没有
return 0;
}
//清空链表中所有的节点
void clear(List* pl)
{
while(-1 != pop_head(pl));
}
//逆序打印链表中的所有节点元素
void reverse_travel_data(List* pl)
{
//1.调用递归函数进行打印
reverse_travel(pl->head);
//2.打印换行符增加美观
printf("\n");
}
//实现逆序打印的递归函数
void reverse_travel(Node* pn)
{
if(pn != NULL)
{
//1.打印后续节点元素值,使用递归
reverse_travel(pn->next);
//2.打印头节点元素值
printf("%d ",pn->data);
}
}
//实现逆转的递归函数
void reverse(Node* pn)
{
// 确保链表中至少有两个节点才需要逆转
if(pn != NULL && pn->next != NULL)
{
//采用递归逆转后续的元素
reverse(pn->next);
//逆转两个节点的方法
pn->next->next = pn;
pn->next = NULL;
}
}
//逆转链表中所有节点
void reverse_data(List* pl)
{
//1.调用递归函数进行逆转
reverse(pl->head);
//2.交换head 和 tail的指向
Node* pt = pl->head;
pl->head = pl->tail;
pl->tail = pt;
}
//删除指定下标位置的节点
int delete_data(List* pl,int pos)
{
//1.判断下标位置是否合法
if(pos < 0 || pos >= size(pl))
{
printf("下标位置不合法,删除失败\n");
return -1;//删除失败
}
//2.当 pos = 0时,删除头节点
if(0 == pos)
{
return pop_head(pl);
}
//3.当 pos = cnt-1时,删除尾节点
if(size(pl)-1 == pos)
{
return pop_tail(pl);
}
//4.当 pos为其他值时,删除中间节点
Node* pt = pl->head;
int i = 0;
for(i = 1; i < pos; i++)
{
pt = pt->next;
}
Node* pm = pt->next;
pt->next = pm->next;
int temp = pm->data;
free(pm);
pm = NULL;
--pl->cnt;
return temp;
}
//删除尾节点的功能函数
int pop_tail(List* pl)
{
//判断链表是否为空
if(empty(pl))
{
return -1;//删除失败
}
//当链表中只有一个节点时
if(1 == size(pl))
{
int temp = pl->head->data;
free(pl->head);
pl->head = pl->tail = NULL;
--pl->cnt;
return temp;
}
//当链表中有更多的节点时,采用归纳法
//先将相对于cnt=2时多出来的next执行完毕
Node* pt = pl->head;
int i = 0;
for(i = 2; i < size(pl); i++)
{
pt = pt->next;
}
//接下来写cnt = 2时 的删除代码
int temp = pl->tail->data;
free(pl->tail);
pl->tail = pt;
// 为了避免记录已经删除节点的地址
pl->tail->next = NULL;
--pl->cnt;
return temp;
}
//实现获取头节点的元素值 get_head
int get_head(List* pl)
{
return empty(pl)?-1:pl->head->data;
}
//实现获取尾节点的元素值 get_tail
int get_tail(List* pl)
{
return empty(pl)?-1:pl->tail->data;
}
//实现删除头节点的功能 pop_head
int pop_head(List* pl)
{
if(empty(pl))
{
return -1;//删除失败
}
Node* pt = pl->head;
int temp = pt->data;
pl->head = pt->next;
free(pt);
pt = NULL;
//当链表中只有一个节点时,tail置为NULL
if(NULL == pl->head)
{
pl->tail = NULL;
}
--pl->cnt;
return temp;
}
//向链表中任意的下标位置插入新元素
void insert_data(List* pl,int pos,int data)
{
//1.判断坐标是否合法
if(pos < 0 || pos > size(pl))
{
//printf("坐标不合法,插入失败\n");
//return;//结束当前函数
//pos = 0; //默认插入到链表的头节点位置
pos = size(pl);//默认插入到链表的尾部
}
//2.将新元素插入指定的位置
if(0 == pos)
{
push_head(pl,data);
return;
}
if(size(pl) == pos)
{
push_tail(pl,data);
return;
}
//接下来就是插入到中间位置的情况
Node* pn = create_node(data);
Node* pt = pl->head;
//使用for循环将相对于pos=1多出来的next走完
int i = 0;
for(i = 1; i < pos; i++)
{
pt = pt->next;
}
//接下来把pos=1时的代码写下来即可
pn->next = pt->next;
pt->next = pn;
//让节点的个数加1
++pl->cnt;
}
//向链表的末尾追加新元素
void push_tail(List* pl,int data)
{
//1.创建新节点
Node* pn = create_node(data);
//2.将新节点插入到链表的末尾
if(empty(pl))
{
pl->head = pn;
}
else
{
pl->tail->next = pn;
}
pl->tail = pn;
//3.将节点的个数 加1
++pl->cnt;
}
//编写创建新节点的函数 create_node
Node* create_node(int data)
{
Node* pn = (Node*)malloc(sizeof(Node));
if(NULL == pn)
{
printf("创建节点失败\n");
//return;
exit(-1);
}
pn->data = data;
pn->next = NULL;
return pn;
}
//判断链表是否为空 empty
int empty(List* pl)
{
return NULL == pl->head;
}
//判断链表是否为满 full
int full(List* pl)
{
return 0;
}
//计算链表中节点个数 size
int size(List* pl)
{
return pl->cnt;
}
//向头节点位置插入新元素的功能 push_head
void push_head(List* pl,int data)
{
//1.创建新节点,初始化
/*
Node* pn = (Node*)malloc(sizeof(Node));
if(NULL == pn)
{
printf("创建节点失败\n");
return;
}
pn->data = data;
pn->next = NULL;
*/
Node* pn = create_node(data);
//2.将新节点插入到头节点的位置
if(empty(pl))
{
pl->head = pl->tail = pn;
}
else
{
pn->next = pl->head;
pl->head = pn;
}
//3.节点元素的个数 加1
++pl->cnt;
}
//遍历链表中的所有节点元素值 travel
void travel(List* pl)
{
printf("链表中的元素有:");
Node* pt = pl->head;
while(pt != NULL)
{
printf("%d ",pt->data);
pt = pt->next;
}
printf("\n");
}
有序二叉树
//编程实现有序二叉树的各种操作
#include <stdio.h>
#include <stdlib.h>
//定义节点的数据类型
typedef struct Node
{
int data;//记录数据元素本身
struct Node* left;//记录左子节点的地址
struct Node* right;//记录右子节点的地址
}Node;
//定义有序二叉树的数据类型
typedef struct
{
Node* root;//记录根节点的地址
int cnt;//记录节点的个数
}Tree;
//向有序二叉树中插入元素
void insert_data(Tree* pt,int data);
//实现插入节点的递归函数
void insert(Node** pRoot,Node* pn);
//采用中序遍历方式来遍历有序二叉树
void travel_data(Tree* pt);
//遍历的递归函数
void travel(Node* pn);
//判断有序二叉树是否为空 empty
int empty(Tree* pt);
//判断有序二叉树是否为满 full
int full(Tree* pt);
//获取根节点的元素值 get_root
int get_root(Tree* pt);
//获取有序二叉树中节点的个数 size
int size(Tree* pt);
//清空有序二叉树中的所有节点
void clear_data(Tree* pt);
//清空的递归函数
void clear(Node** ppn);
//查找指向目标元素指针的地址
Node** find_data(Tree* pt,int data);
//查找的递归函数
Node** find(Node** ppn,int data);
//删除指定的元素
int delete_data(Tree* pt,int data);
//修改指定的元素
void modify_data(Tree* pt,int old_data,int new_data);
int main(void)
{
//创建有序二叉树,并且进行初始化
Tree tree;
tree.root = NULL;
tree.cnt = 0;
insert_data(&tree,50);
travel_data(&tree);//50
insert_data(&tree,70);
travel_data(&tree);//50 70
insert_data(&tree,20);
travel_data(&tree);//20 50 70
insert_data(&tree,60);
travel_data(&tree);//20 50 60 70
insert_data(&tree,40);
travel_data(&tree);//20 40 50 60 70
printf("--------------------------\n");
printf("%s\n",empty(&tree)?"有序二叉树已经空了":"有序二叉树没有空");//有序二叉树没有空
printf("%s\n",full(&tree)?"有序二叉树已经满了":"有序二叉树没有满");//有序二叉树没有满
printf("有序二叉树的根节点元素是:%d\n",get_root(&tree));// 50
printf("有序二叉树中节点元素的个数是:%d\n",size(&tree));// 5
printf("-------------------------\n");
travel_data(&tree);//20 40 50 60 70
delete_data(&tree,50);
travel_data(&tree);//20 40 60 70
delete_data(&tree,40);
travel_data(&tree);//20 60 70
modify_data(&tree,20,40);
travel_data(&tree);//40 60 70
printf("-------------------------\n");
clear_data(&tree);
travel_data(&tree); // 啥也没有
return 0;
}
//修改指定的元素
void modify_data(Tree* pt,int old_data,int new_data)
{
//1.删除旧元素
int res = delete_data(pt,old_data);
if(-1 == res)
{
printf("目标元素不存在,修改失败\n");
return;
}
//2.插入新元素
insert_data(pt,new_data);
}
//删除指定的元素
int delete_data(Tree* pt,int data)
{
//查找目标元素所在的地址信息
Node** ppn = find_data(pt,data);
if(NULL == *ppn)
{
return -1;//删除失败
}
//将要删除节点的左子树合并到右子树中
if((*ppn)->left != NULL)
{
insert(&(*ppn)->right,(*ppn)->left);
}
//寻找临时指针记录要删除的节点地址
Node* pn = *ppn;
//将指向要删除节点的指针指向它的右子树
*ppn = (*ppn)->right;
//释放要删除的节点
free(pn);
pn = NULL;
//节点的个数减 1
--pt->cnt;
return 0;//删除成功
}
//查找指向目标元素指针的地址
Node** find_data(Tree* pt,int data)
{
//调用递归函数进行查找
return find(&pt->root,data);
}
//查找的递归函数
Node** find(Node** ppn,int data)
{
//如果有序二叉树为空,查找失败
if(NULL == *ppn)
{
return ppn;
}
//如果目标元素和根元素相等,则查找成功
else if(data == (*ppn)->data)
{
return ppn;
}
//如果目标元素小于根元素,则查找左子树
else if(data < (*ppn)->data)
{
return find(&(*ppn)->left,data);
}
//如果目标元素大于根元素,则查找右子树
else
{
return find(&(*ppn)->right,data);
}
}
//清空的递归函数
void clear(Node** ppn)
{
if(*ppn != NULL)
{
//1.清空左子树
clear(&(*ppn)->left);
//2.清空右子树
clear(&(*ppn)->right);
//3.释放根节点
free(*ppn);
*ppn = NULL;
}
}
//清空有序二叉树中的所有节点
void clear_data(Tree* pt)
{
//调用递归函数来释放所有的节点
clear(&pt->root);
//节点个数 置为0
pt->cnt = 0;
}
//判断有序二叉树是否为空 empty
int empty(Tree* pt)
{
return NULL == pt->root;
}
//判断有序二叉树是否为满 full
int full(Tree* pt)
{
return 0;
}
//获取根节点的元素值 get_root
int get_root(Tree* pt)
{
return empty(pt)?-1:pt->root->data;
}
//获取有序二叉树中节点的个数 size
int size(Tree* pt)
{
return pt->cnt;
}
//遍历的递归函数
void travel(Node* pn)
{
if(pn != NULL)
{
//1.遍历左子树,使用递归
travel(pn->left);
//2.遍历根节点
printf("%d ",pn->data);
//3.遍历右子树,使用递归
travel(pn->right);
}
}
//采用中序遍历方式来遍历有序二叉树
void travel_data(Tree* pt)
{
printf("有序二叉树中的元素有:");
//调用递归函数实现遍历
travel(pt->root);
printf("\n");
}
//实现插入节点的递归函数
void insert(Node** pRoot,Node* pn)
{
// Node** pRoot = &pt->root;
// pRoot = &pt->root;
// *pRoot = *(&pt->root) = pt->root;
//1.如果有序二叉树为空,则直接指向新节点
if(NULL == *pRoot)
{
*pRoot = pn;
return;
}
//2.如果新节点的元素值小于根节点,则插入到左子树,使用递归
else if(pn->data < (*pRoot)->data)
{
insert(&(*pRoot)->left,pn);
}
//3.如果新节点的元素值大于等于根节点,则插入到右子树中,使用递归
else
{
insert(&(*pRoot)->right,pn);
}
}
//向有序二叉树中插入元素
void insert_data(Tree* pt,int data)
{
//1.创建新节点,并且进行初始化
Node* pn = (Node*)malloc(sizeof(Node));
if(NULL == pn)
{
printf("创建新节点失败\n");
return;
}
pn->data = data;
pn->left = NULL;
pn->right = NULL;
//2.将新节点插入到合适的位置上,调用递归
insert(&pt->root,pn);
//3.节点的个数 加1
++pt->cnt;
}
参考资料





 浙公网安备 33010602011771号
浙公网安备 33010602011771号