笔试常考题型之二叉树的遍历
一、介绍
在互联网公司的笔试题中,经常会出现给出一个二叉树的前序和中序遍历,让你去求它的后序遍历问题,因此我将这类题型的解题步骤总结如下。
二、例题

题目解析:
注:此题中f节点的爸爸是d。
前序遍历顺序 根->左->右:abefd。
中序遍历顺序 左->根->右:ebadf。
后序遍历顺序 左->右->根:ebfda。

题目解析:
二叉搜索树有一个很重要的特性:树中任何结点的左子树中所有结点的值均比该结点小,右子树中所有结点的值均比该结点大。对二叉搜索树进行中序遍历即得到一个递增排序的序列。
因此,检查一个树是否是二叉搜索树可以使用中序遍历,根据递增排序的序列生成二权搜索树也可以使用中序遍历。
参考资料:二叉搜索树的简单介绍 二叉排序_搜索_查找树 C++
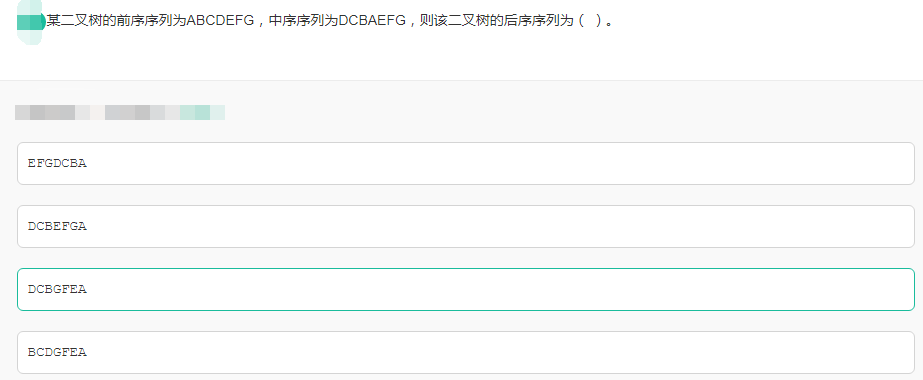
题目解析:
1,先序遍历的第一个节点肯定是根节点,所以A为该二叉树的根节点。
2,中序遍历中根节点左侧的节点全是根节点左子树的节点,根节点右侧的节点全是根节点的右子树。所以我们可以分成 DCB(左) | A(根) | EFG(右)。
3,递归使用上述两个步骤,可以画出整个二叉树。
(1)先得出A是根节点。
(2)DCB是A左子树中的点,EFG是A右子树中的点。
(1)B是A左子树的根节点,E是A右子树的根节点。
(2)CD是B左子树中的点,FG是E右子树中的点。
(1)C是B左子树的根节点,F是E右子树的根节点。
(2)D是C左子树中的点,G是F右子树中的点。
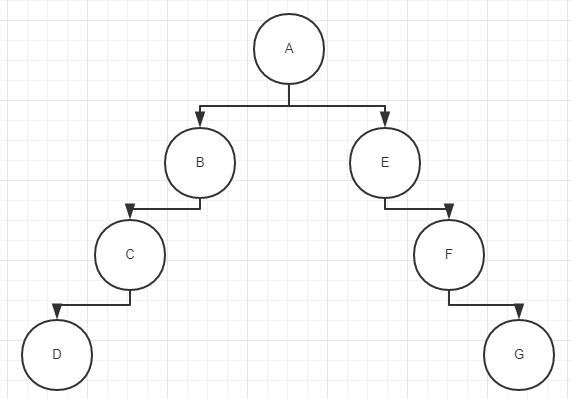
因此该二叉树的后序遍历为(左->右->根):DCBGFEA。
三、解题感受
遇到这种问题,记得先找出根节点,然后找出根节点左边的节点和根节点右边的节点,然后以此类推,找出根节点左子树的根节点和右子树的根节点...最后可以根据前序和中序遍历画出一个二叉树,再根据画出的二叉树(前提是要保证之前的步骤都正确)求出后序遍历。





 浙公网安备 33010602011771号
浙公网安备 33010602011771号