2014年第五届蓝桥杯C/C++B组省赛题目解析
一、啤酒和饮料
啤酒每罐2.3元,饮料每罐1.9元。小明买了若干啤酒和饮料,一共花了82.3元。
我们还知道他买的啤酒比饮料的数量少,请你计算他买了几罐啤酒。
注意:答案是一个整数。请通过浏览器提交答案。
不要书写任何多余的内容(例如:写了饮料的数量,添加说明文字等)。
分析:此题可用循环暴力求解出结果。
数值先都扩大十倍,方便计算。
全部啤酒罐数:823/23=35.78;全部饮料罐数:823/19=43.31;啤酒和饮料对半罐数:823/42=19.59
设啤酒x,饮料y,则根据上述计算可知,x<y,20<=y<=43
#include<stdio.h> #include <cstdio> #include <cmath> using namespace std; int main(){ for(int x = 1;x < 19;x++){ for(int y = 19;y <= 43;y++){ if(fabs(23*x + 19*y - 823) <= 1e-3 && x<y) { printf("%d %d\n",x,y); //输出啤酒与饮料的罐数 } } } return 0; }
答案:11.
二、切面条
一根高筋拉面,中间切一刀,可以得到2根面条。
如果先对折1次,中间切一刀,可以得到3根面条。
如果连续对折2次,中间切一刀,可以得到5根面条。
那么,连续对折10次,中间切一刀,会得到多少面条呢?
答案是个整数,请通过浏览器提交答案。不要填写任何多余的内容。
分析:观察得到的面条数,发现规律 f[n]=2*f[n-1]-1。因此我们可以通过循环计算出答案
#include <stdio.h> long f[12]; int main(){ f[0]=2; for(int i = 1;i <= 10;i++){ f[i] = 2*f[i-1] - 1; } printf("%ld\n",f[10]); }
答案:1025.
三、李白打酒
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒2斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店5次,遇到花10次,已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白遇到店和花的次序,可以把遇店记为a,遇花记为b。则:babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢?请你计算出所有可能方案的个数(包含题目给出的)。
注意:通过浏览器提交答案。答案是个整数。不要书写任何多余的内容。
分析1:全排列,循环判断。参考资料 next_permutation
#include <stdio.h> #include <algorithm> using namespace std; int f[16]; int main(){ int i,j,tot=0; for(i = 0;i < 5;i++) f[i] = 0; for(;i < 15;i++){ f[i] = 1; } do{ int ans=2; bool error=false; for(j = 0;j < 15;j++){ if(f[j] == 0) ans *= 2; else if(f[j] == 1) ans -= 1; if(ans < 0){ error = true; break; } } if(error) continue; if(ans==0){ tot++; } }while(next_permutation(f,f+14)); //求数列的全排列 printf("%d\n",tot); return 0; }
分析2:运用DFS算法,当遇见店时酒乘一倍,遇见花时酒减1,直到店和花都为0时,输出酒的数值。
#include <stdio.h> int tot=0; void dfs(int dian,int hua,int jiu){ if(dian==0 && hua==0 && jiu==1){ tot++; return ; } if(dian > 0) dfs(dian-1,hua,jiu*2); if(jiu>0 && hua>0) dfs(dian,hua-1,jiu-1); } int main(){ int n; dfs(5,9,2); printf("%d\n",tot); return 0; }
答案:14
四、史丰收速算
史丰收速算法的革命性贡献是:从高位算起,预测进位。不需要九九表,彻底颠覆了传统手算!
速算的核心基础是:1位数乘以多位数的乘法。
其中,乘以7是最复杂的,就以它为例。
因为,1/7 是个循环小数:0.142857...,如果多位数超过 142857...,就要进1
同理,2/7, 3/7, ... 6/7 也都是类似的循环小数,多位数超过 n/7,就要进n
下面的程序模拟了史丰收速算法中乘以7的运算过程。
乘以 7 的个位规律是:偶数乘以2,奇数乘以2再加5,都只取个位。
乘以 7 的进位规律是:
满 142857... 进1,
满 285714... 进2,
满 428571... 进3,
满 571428... 进4,
满 714285... 进5,
满 857142... 进6
请分析程序流程,填写划线部分缺少的代码。
//计算个位 int ge_wei(int a) { if(a % 2 == 0) return (a * 2) % 10; else return (a * 2 + 5) % 10; } //计算进位 int jin_wei(char* p) { char* level[] = { "142857", "285714", "428571", "571428", "714285", "857142" }; char buf[7]; buf[6] = '\0'; strncpy(buf,p,6); int i; for(i=5; i>=0; i--){ int r = strcmp(level[i], buf); if(r<0) return i+1; while(r==0){ p += 6; strncpy(buf,p,6); r = strcmp(level[i], buf); if(r<0) return i+1; ______________________________; //填空 } } return 0; } //多位数乘以7 void f(char* s) { int head = jin_wei(s); if(head > 0) printf("%d", head); char* p = s; while(*p){ int a = (*p-'0'); int x = (ge_wei(a) + jin_wei(p+1)) % 10; printf("%d",x); p++; } printf("\n"); } int main() { f("428571428571"); f("34553834937543"); return 0; }

#include <cstring> #include <cstdio> using namespace std; //计算个位 int ge_wei(int a) { if(a % 2 == 0) return (a * 2) % 10; else return (a * 2 + 5) % 10; } //计算进位 int jin_wei(char* p) { char* level[] = { "142857", "285714", "428571", "571428", "714285", "857142" }; char buf[7]; buf[6] = '\0'; strncpy(buf,p,6); int i; for(i=5; i>=0; i--){ int r = strcmp(level[i], buf); if(r<0) return i+1; while(r==0){ p += 6; strncpy(buf,p,6); r = strcmp(level[i], buf); if(r<0) return i+1; if(r>0) return i; //填空 } } return 0; } //多位数乘以7 void f(char* s) { int head = jin_wei(s); if(head > 0) printf("%d", head); char* p = s; while(*p){ int a = (*p-'0'); int x = (ge_wei(a) + jin_wei(p+1)) % 10; printf("%d",x); p++; } printf("\n"); } int main() { f("428571428571"); f("34553834937543"); return 0; }
答案:if(r>0) return i;
五、打印图形
小明在X星球的城堡中发现了如下图形和文字:
rank=3
rank=5
ran=6
小明开动脑筋,编写了如下的程序,实现该图形的打印。
#define N 70 void f(char a[][N], int rank, int row, int col) { if(rank==1){ a[row][col] = '*'; return; } int w = 1; int i; for(i=0; i<rank-1; i++) w *= 2; ____________________________________________; f(a, rank-1, row+w/2, col); f(a, rank-1, row+w/2, col+w); } int main() { char a[N][N]; int i,j; for(i=0;i<N;i++) for(j=0;j<N;j++) a[i][j] = ' '; f(a,6,0,0); for(i=0; i<N; i++){ for(j=0; j<N; j++) printf("%c",a[i][j]); printf("\n"); } return 0; }

#include <stdio.h> #define N 70 void f(char a[][N], int rank, int row, int col) { if(rank==1){ a[row][col] = '*'; return; } int w = 1; int i; for(i=0; i<rank-1; i++) w *= 2; f(a, rank-1, row, col+w/2); //填空 f(a, rank-1, row+w/2, col); f(a, rank-1, row+w/2, col+w); } int main() { char a[N][N]; int i,j; for(i=0;i<N;i++) for(j=0;j<N;j++) a[i][j] = ' '; f(a,6,0,0); for(i=0; i<N; i++){ for(j=0; j<N; j++) printf("%c",a[i][j]); printf("\n"); } return 0; }
答案:f(a, rank-1, row, col+w/2);
六、奇怪的分式
上小学的时候,小明经常自己发明新算法。一次,老师出的题目是:
1/4 乘以 8/5
小明居然把分子拼接在一起,分母拼接在一起,答案是:18/45 (参见图1.png)
老师刚想批评他,转念一想,这个答案凑巧也对啊,真是见鬼!
对于分子、分母都是 1~9 中的一位数的情况,还有哪些算式可以这样计算呢?
请写出所有不同算式的个数(包括题中举例的)。
显然,交换分子分母后,例如:4/1 乘以 5/8 是满足要求的,这算做不同的算式。
但对于分子分母相同的情况,2/2 乘以 3/3 这样的类型太多了,不在计数之列!
注意:答案是个整数(考虑对称性,肯定是偶数)。请通过浏览器提交。不要书写多余的内容。

分析:先试着简单模拟,然后暴力破解法求出答案。
#include <stdio.h> #include <cstring> using namespace std; int main(){ int tot=0; for(int a=1;a<=9;a++){ for(int b=1;b<=9;b++){ for(int c=1;c<=9;c++){ for(int d=1;d<=9;d++){ if(a!=b && c!=d){ if(a*c*(b*10+d) == b*d*(a*10+c)) { tot++; printf("%d/%d * %d/%d= %d/%d\n",a,b,c,d,a*10+c,b*10+d); } } } } } } printf("tot=%d\n",tot); return 0; }
答案:14.
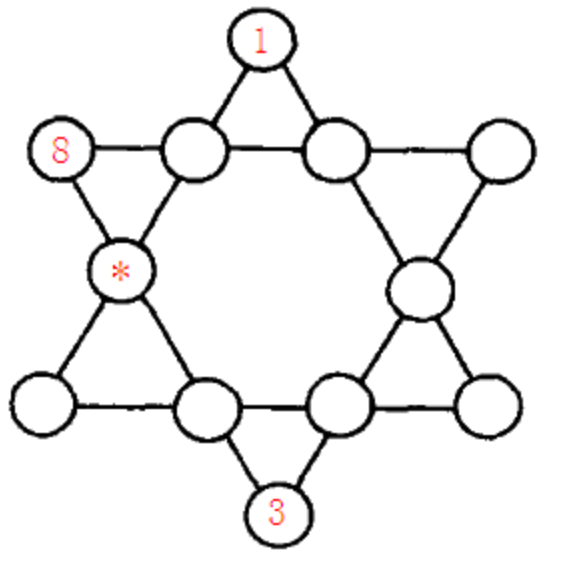
七、六角填数
如图所示六角形中,填入1~12的数字。
使得每条直线上的数字之和都相同。
图中,已经替你填好了3个数字,请你计算星号位置所代表的数字是多少?
请通过浏览器提交答案,不要填写多余的内容。
分析:暴力求解。
#include <cstring> #include <algorithm> #include <iostream> using namespace std; int f[13]; //储存十二个数字 int x[6]; //共六条线 int main(){ int k=0; for(int i=2;i<=12;i++){ if(i!=3 && i!=8) f[k++]=i; } do{ bool error =false; int m,n; x[0]=8+f[0]+f[7]+3; x[1]=f[8]+1+f[0]+f[1]; x[2]=8+f[1]+f[2]+f[3]; x[3]=1+f[2]+f[4]+f[5]; x[4]=3+f[3]+f[4]+f[6]; x[5]=f[5]+f[6]+f[7]+f[8]; for(m=0;m<=4;m++){ for(n=m+1;n<=5;n++){ if(x[m] != x[n]){ error=true; break; } } if(error) break; } if(m==5 && n==6 && error==false) for(int k=0;k<=9;k++) printf("%d ",f[k]); }while(next_permutation(f,f+9)); for(int i=2;i<=12;i++){ if(i!=3&&i!=8) f[k++]=i; } return 0; }
答案:10
八、蚂蚁感冒
长100厘米的细长直杆子上有n只蚂蚁。它们的头有的朝左,有的朝右。
每只蚂蚁都只能沿着杆子向前爬,速度是1厘米/秒。
当两只蚂蚁碰面时,它们会同时掉头往相反的方向爬行。
这些蚂蚁中,有1只蚂蚁感冒了。并且在和其它蚂蚁碰面时,会把感冒传染给碰到的蚂蚁。
请你计算,当所有蚂蚁都爬离杆子时,有多少只蚂蚁患上了感冒。
【数据格式】
第一行输入一个整数n (1 < n < 50), 表示蚂蚁的总数。
接着的一行是n个用空格分开的整数 Xi (-100 < Xi < 100), Xi的绝对值,表示蚂蚁离开杆子左边端点的距离。正值表示头朝右,负值表示头朝左,数据中不会出现0值,也不会出现两只蚂蚁占用同一位置。其中,第一个数据代表的蚂蚁感冒了。
要求输出1个整数,表示最后感冒蚂蚁的数目。
例如,输入:
3
5 -2 8
程序应输出:
1
再例如,输入:
5
-10 8 -20 12 25
程序应输出:
3
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
思路:
- 首先一定要记住蚂蚁都具有相同的速度,所以他们的相对位置不会变!
- 我们可以从第一只那只感冒的蚂蚁入手,实际上,如果第一只蚂蚁向右爬,则它出发的位置右边的蚂蚁中向左爬且离第一只蚂蚁最近的那只会被传染,然后双方会掉头爬行。
- 接下来,第一只蚂蚁左边的蚂蚁中向右爬行且离第一只蚂蚁最近的那只会被传染,双方再掉头。而对于一开始第一只被传染的那只蚂蚁来说,它会传染给他右边向左爬且最近的蚂蚁……
#include<stdio.h> #include<string.h> struct Node { int pos,dir; } Node[55]; int main() { int n,ans=1; scanf("%d",&n); memset(Node,0,sizeof(Node)); for(int i=0; i<n; i++) { scanf("%d",&Node[i].pos); if(Node[i].pos>0) Node[i].dir=1; else { Node[i].dir=-1; Node[i].pos*=-1; //在此强调:正负仅仅表示方向,位置是其绝对值 } } int turn=0; //考虑到第一只感冒的蚂蚁可能不会掉头的情况,设置标记turn,初始化为0 if(Node[0].dir==1) { for(int i=1; i<n; i++) { if((Node[i].pos>Node[0].pos) && (Node[i].dir==-1)) { turn=1;//第一只感冒的蚂蚁遇到迎面而来的蚂蚁,它将掉头,将turn标记为1 ans++; } } for(int i=1; i<n; i++) { if((Node[i].pos<Node[0].pos) && (Node[i].dir==1) && turn)//只有第一只蚂蚁掉头了,才会与另一方向前进的蚂蚁出现碰头的情形,因此注意加上turn是否为1的判断 ans++; } } else { for(int i=1; i<n; i++) { if((Node[i].pos<Node[0].pos) && (Node[i].dir==1)) { turn=1; ans++; } } for(int i=1; i<n; i++) { if((Node[i].pos>Node[0].pos) && (Node[i].dir==-1) && turn) ans++; } } printf("%d\n",ans); return 0; }

#include <stdio.h> struct mayi { int direct; //0为左,1为右 int dist; //距离左端点距离 int cold; //0为正常,1为感冒 } ; int main() { int n,i,sign,j,num=0; scanf("%d",&n); struct mayi a[n]; for(i=0;i<n;i++) { scanf("%d",&a[i].dist); a[i].dist*=2; a[i].direct=1; a[i].cold=0; if(a[i].dist<0) { a[i].dist*=-1; a[i].direct=0; } a[0].cold=1; } for(;;) { sign=0; for(i=0;i<n;i++) //所有蚂蚁走路 { if(a[i].direct==0) a[i].dist--; else a[i].dist++; } for(i=0;i<n-1;i++) for(j=i+1;j<n;j++) { if(a[i].dist==a[j].dist) { if(a[i].direct==0) {a[i].direct=1;} else a[i].direct=0; if(a[j].direct==0) {a[j].direct=1;} else a[j].direct=0; if(a[i].cold==1 ) a[j].cold=1; if(a[j].cold==1 ) a[i].cold=1; } } for(i=0;i<n;i++) { if(a[i].dist>=0 && a[i].dist<=200) { sign=1; break; } } if(sign==0) break; } for(i=0;i<n;i++) if(a[i].cold==1) num++; printf("%d\n",num); return 0; }
九、地宫取宝
X 国王有一个地宫宝库。是 n x m 个格子的矩阵。每个格子放一件宝贝。每个宝贝贴着价值标签。
地宫的入口在左上角,出口在右下角。
小明被带到地宫的入口,国王要求他只能向右或向下行走。
走过某个格子时,如果那个格子中的宝贝价值比小明手中任意宝贝价值都大,小明就可以拿起它(当然,也可以不拿)。
当小明走到出口时,如果他手中的宝贝恰好是k件,则这些宝贝就可以送给小明。
请你帮小明算一算,在给定的局面下,他有多少种不同的行动方案能获得这k件宝贝。
【数据格式】
输入一行3个整数,用空格分开:n m k (1<=n,m<=50, 1<=k<=12)
接下来有 n 行数据,每行有 m 个整数 Ci (0<=Ci<=12)代表这个格子上的宝物的价值
要求输出一个整数,表示正好取k个宝贝的行动方案数。该数字可能很大,输出它对 1000000007 取模的结果。
例如,输入:
2 2 2
1 2
2 1
程序应该输出:
2
再例如,输入:
2 3 2
1 2 3
2 1 5
程序应该输出:
14
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
解法1,DFS搜索
#include<stdio.h> long long ans; int n,m,k; int a[55][55]; const int INF=0x3f3f3f3f; void dfs(int x,int y,int pre,int max) { if(pre>k) return ; if(x==n-1 && y==m-1) { if(pre==k||(pre==k-1&&max<a[x][y])) //走到终点时刚好拿到了K件礼物或者拿到了k-1件礼物,在该点的礼物的价值又大于之前拿到的最大价值。此时方案数加一。 ans++; return ; } if(x < n-1)//向下走 { if(a[x][y]>max) dfs(x+1,y,pre+1,a[x][y]); dfs(x+1,y,pre,max); } if(y < m-1)//向右走 { if(a[x][y]>max) dfs(x,y+1,pre+1,a[x][y]); dfs(x,y+1,pre,max); } } int main() { while(~scanf("%d%d%d",&n,&m,&k)) //循环从输入流读取m、n、k,直到遇到EOF为止,等同于 while (scanf("%d%d",&m,&n)!=EOF) { for(int i=0; i<n; i++) for(int j=0; j<m; j++) scanf("%d",&a[i][j]); ans=0; dfs(0,0,0,-INF); printf("%lld\n",ans%1000000007); } return 0; }
解法2,记忆化搜索
#include<stdio.h> #include<string.h> int n,m,k; int a[55][55][15][15]; int map[55][55]; int dfs(int x,int y,int pre,int max) { if(a[x][y][pre][max+1]>=0) return a[x][y][pre][max+1]; int sum=0; if(x==n-1&&y==m-1) { if(pre==k||(pre==k-1&&max<map[x][y])) { sum++; sum%=1000000007; } a[x][y][pre][max+1]=sum; return a[x][y][pre][max+1]; } if(x<n-1) { if(map[x][y]>max) sum+=dfs(x+1,y,pre+1,map[x][y]); sum+=dfs(x+1,y,pre,max); sum%=1000000007; } if(y<m-1) { if(map[x][y]>max) sum+=dfs(x,y+1,pre+1,map[x][y]); sum+=dfs(x,y+1,pre,max); sum%=1000000007; } a[x][y][pre][max+1]=sum%1000000007; return a[x][y][pre][max+1]; } int main() { while(~scanf("%d%d%d",&n,&m,&k)) //循环从输入流读取m、n、k,直到遇到EOF为止,等同于 while (scanf("%d%d",&m,&n)!=EOF) { memset(a,-1,sizeof(a)); for(int i=0; i<n; i++) for(int j=0; j<m; j++) scanf("%d",&map[i][j]); dfs(0,0,0,-1); printf("%lld\n",a[0][0][0][0]%1000000007); } return 0; }

#include<stdio.h> #include<string.h> #define N 55 #define MOD 1000000007 int map[55][55]; int dp[55][55][15][15]; int main(void) { int n, m, k; int i, j, c, val, aMax; scanf("%d%d%d", &n, &m, &k); aMax = 0; for(i = 1; i <= n; i++) { for(j = 1; j <= m; j++) { scanf("%d", &map[i][j]); // map[i][j]++; if(aMax < map[i][j]) { aMax = map[i][j]; } } } memset(dp, 0, sizeof(dp)); dp[1][1][0][0] = 1; dp[1][1][1][map[1][1]] = 1; for(i = 1; i <= n; i++) { for(j = 1; j <= m; j++) { dp[i][j][0][0] += dp[i][j - 1][0][0] + dp[i - 1][j][0][0]; dp[i][j][0][0] %= MOD; for(c = 1; c <= k; c++) { for(val = 0; val <= aMax; val++) { dp[i][j][c][val] += dp[i][j - 1][c][val] + dp[i - 1][j][c][val]; dp[i][j][c][val] %= MOD; } if(c == 1) { dp[i][j][1][map[i][j]] += dp[i][j - 1][0][0]; dp[i][j][1][map[i][j]] %= MOD; dp[i][j][1][map[i][j]] += dp[i - 1][j][0][0]; dp[i][j][1][map[i][j]] %= MOD; } else { for(val = 0; val < map[i][j]; val++) { dp[i][j][c][map[i][j]] += dp[i][j - 1][c - 1][val]; dp[i][j][c][map[i][j]] %= MOD; dp[i][j][c][map[i][j]] += dp[i - 1][j][c - 1][val]; dp[i][j][c][map[i][j]] %= MOD; } } } } } int sum = 0; for(i = 0; i <= aMax; i++) { sum += dp[n][m][k][i]; sum %= MOD; } printf("%d", sum); return 0; }
十、小朋友排队
n 个小朋友站成一排。现在要把他们按身高从低到高的顺序排列,但是每次只能交换位置相邻的两个小朋友。
每个小朋友都有一个不高兴的程度。开始的时候,所有小朋友的不高兴程度都是0。
如果某个小朋友第一次被要求交换,则他的不高兴程度增加1,如果第二次要求他交换,则他的不高兴程度增加2(即不高兴程度为3),依次类推。当要求某个小朋友第k次交换时,他的不高兴程度增加k。
请问,要让所有小朋友按从低到高排队,他们的不高兴程度之和最小是多少。
如果有两个小朋友身高一样,则他们谁站在谁前面是没有关系的。
【数据格式】
输入的第一行包含一个整数n,表示小朋友的个数。
第二行包含 n 个整数 H1 H2 … Hn,分别表示每个小朋友的身高。
输出一行,包含一个整数,表示小朋友的不高兴程度和的最小值。
例如,输入:
3
3 2 1
程序应该输出:
9
【样例说明】
首先交换身高为3和2的小朋友,再交换身高为3和1的小朋友,再交换身高为2和1的小朋友,每个小朋友的不高兴程度都是3,总和为9。
【数据规模与约定】
对于10%的数据, 1<=n<=10;
对于30%的数据, 1<=n<=1000;
对于50%的数据, 1<=n<=10000;
对于100%的数据,1<=n<=100000,0<=Hi<=1000000。
资源约定:
峰值内存消耗 < 256M
CPU消耗 < 1000ms
请严格按要求输出,不要画蛇添足地打印类似:“请您输入...” 的多余内容。
所有代码放在同一个源文件中,调试通过后,拷贝提交该源码。
注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准,不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>, 不能通过工程设置而省略常用头文件。
提交时,注意选择所期望的编译器类型。
#include<stdio.h> int h[100100]; int un[100100]; int b[1000100]; int reb[1000100]; int Lowbit(int x){ return x&(x^(x-1)); } int sum(int bit[], int idx){ int ret = 0; while(idx > 0){ ret += bit[idx]; idx -= Lowbit(idx); } return ret; } void add(int bit[], int idx, int val){ while(idx < 1000100){ bit[idx] += val; idx += Lowbit(idx); } } long long uVal[100100]; int main(void){ int n, i; scanf("%d", &n); uVal[0] = 0; for(i = 0; i < n; i++){ scanf("%d", &h[i]); h[i]++; uVal[i + 1] = uVal[i] + i + 1; un[i] += i - sum(b, h[i]); add(b, h[i], 1); } long long ans = 0; for(i = n - 1; i >= 0; i--){ un[i] += sum(reb, h[i] - 1); add(reb, h[i], 1); ans += uVal[un[i]]; } printf("%I64d\n", ans); return 0; }






 浙公网安备 33010602011771号
浙公网安备 33010602011771号