牛客网平台常州大学新生寒假训练会试

A-添加逗号

链接：https://www.nowcoder.net/acm/contest/78/A
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

对于一个较大的整数 N(1<=N<=2,000,000,000)

比如 980364535，我们常常需要一位一位数这个数字是几位数，但是如果在这个数字每三位加一个逗号，它会变得更加易于朗读。

因此，这个数字加上逗号成如下的模样：980,364,535请写一个程序帮她完成这件事情

输入描述:

一行一个整数 N

输出描述:

一行一个字符串表示添加完逗号的结果

示例1

输入

980364535

输出

980,364,535

备注:

1≤n≤2,000,000,000

考察内容：数字拆分，字符串处理，细节处理。

#include <bits/stdc++.h>

using namespace std;

int main(){
    int n, i, x[100005], j, m, y, q;
        scanf("%d",&n);
        i = 0;
        m = 0;
        while(n > 0){
            x[i] = n % 10;
            n = n/10;
            i++;
        }
        y = i;
        while(i > 3){
            i = i - 3;
            m++;
        }
        for(j = y - 1;j >= y - i;--j){
            cout << x[j];
        }
        for(j = 0;j < m;++j){
            cout << ",";
            for(q = 0;q < 3;++q){
                cout << x[y - i - 1];
                i++;
            }
        }
        cout << endl;
    
    return 0;
}

A题C++

B-对称

链接：https://www.nowcoder.net/acm/contest/78/B
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

萌新AA喜欢对称，最近她喜欢把棋子放进她的棋盘中，这个棋盘是由 N×M 个格子构成的(1 <= N <= 1,000,000,000;1<=M<=1,000,000,000) 为了保证对称，AA 会以这样的方式摆放她的棋子。她把棋子放在棋盘正中央的方格内，如果不存在这样的方格，她就会停止。然后她以这个方格为中心把棋盘分成四部分，然后对于每个小棋盘进行上述的操作。下面是一个 N=7,M=15 的例子，其中'C'表示棋子

这样子，需要 21个棋子。如果 N=M=5 的话，AA只需要摆放一个棋子，因为分成的四个小棋盘分别是 2×2 的大小，无法在放进去新的棋子。现在，请你帮助 AA来计算，需要多少个棋子。

输入描述:

一行两个整数 N,M

输出描述:

一行一个整数，即需要的棋子数

示例1

输入

7  15

输出

示例2

输入

3 1

输出

说明

不一定变成4个部分，存在中心位置即可

备注:

1≤n,m≤1,000,000,000。

题解：找规律，很容易发现只有 m,n 为奇数时才能找到中心，然后模拟统计即可。

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

long long chen(int n)
{
     int i;
     long long s=1;
     for (i=1;i<=n;++i)
         s*=4;
     return s;
} 

int main()
{
      int n,m,i=0;
      long long s=0;
      scanf("%d %d",&n,&m);
      while (n>1 || m>1){
            if (n%2==0||m%2==0) break;
            s+=chen(i);
            n/=2; m/=2;
            i++;
      }
      if (m==1&&n==1)s+=chen(i);
      cout<<s<<endl;
      return 0; 
}

B题C++

C-竞赛技巧

链接：https://www.nowcoder.net/acm/contest/78/C
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

在ACM竞赛中，当遇到有两个队伍（人）解出相同的题目数量的时候，我们需要通过他们解决问题的总时间进行排序。

一共有 N(1<=N<=5,000)条时间被以时(0<=Hours<=99)，分(0<=Minutes<=59)，秒(0<=Seconds<=59)的形式记录。

你必须要把他们按时，分，秒排序为升序，最少的时间最先。考虑到如下的样例，这三个解出相同题目数量的时间为

11:20:20

11:15:12

14:20:14

正确的排序结果应该是这样的：

11:15:12

11:20:20

14:20:14

输入描述:

第 1 行，一个整数 N 第 2~n+1 行，每行 3 个整数，表示时，分，秒

输出描述:

共 n 行，每行 3 个整数，表示排序完后的结果

示例1

输入

输出

11 15 12 
11 20 20 
14 20 14

说明

所以在保证能做对的情况下，我们应当尽量减少罚时

考察内容：排序

#include<iostream>  
#include<algorithm>  
#include<cstdio>

using namespace std;  

int n;  

struct Time {     
         int h,m,s;  
} t[5000];  

bool comp (Time t1, Time t2) {  
     return t1.h < t2.h ||   
        (t1.h == t2.h && t1.m<t2.m) ||   
        (t1.h == t2.h && t1.m == t2.m && t1.s<t2.s);       
}  

int main () {  

     cin >> n;  
     for (int i = 0; i < n; i++)  
         cin >> t[i].h >> t[i].m >> t[i].s;  

     for (int i = 0; i < n-1; i++) {  
         int min = i;  
         for (int j = i+1; j < n; j++)  
             if (comp(t[j],t[min])) min = j;  
         Time tmp = t[i];  
         t[i] = t[min],t[min] = tmp;  
     }  


     for (int i = 0; i < n; i++)  
            cout << t[i].h << " " << t[i].m <<" " << t[i].s << "\n";  

    return 0;
}

C题C++冒泡排序

#include<bits/stdc++.h>
using namespace std;
struct sam
{
    int x,y,z;
};
int cmp(sam &p,sam &q)
{
    return (p.x<q.x||(p.x==q.x&&p.y<q.y)||(p.x==q.x&&p.y==q.y&&p.z<q.z));
}
int main()
{
    int n,i;
    sam a[10000];
    scanf("%d",&n);
    for (i=1;i<=n;i++)
        scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
    sort(a+1,a+1+n,cmp);
    for (i=1;i<=n;i++)
        printf("%d %d %d\n",a[i].x,a[i].y,a[i].z);
}

C题C++Sort()

D-训练技巧

链接：https://www.nowcoder.net/acm/contest/78/D
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

常州大学组织了新生寒假训练一共N天，每天训练可以获得的训练效果是Ei。但是如果连续训练超过K天，萌新们会受不了而被劝退。

现在负责人想知道，如何安排能保证萌新不会被劝退并且能获得最大的训练效果。

输入描述:

第一行：两个用空格隔开的整数：N和K，1≤N≤100000，1≤K≤N
第二行到N+1行：第i+1行有一个整数，表示第N天的训练效果是Ei，(0 <= Ei <= 1,000,000,000）

输出描述:

第一行：单个整数，表示最大的能力之和

示例1

输入

输出

说明

（除了第三天以外每天都在训练，总训练效果为1+2+4+5=12）

备注:

1≤n≤100,000

考察内容：动态规划，单调队列。

题解：这题应该是个经典的动态规划问题（原题），用单调队列优化。
用 dp[i]表示不取 i，且取法合法的最小损失，那么 dp[i]=min{dp[j]+a[i]}，其中 i-j<=k。
注意到可以用单调队列优化。我们用 q[i]表示目前符合条件的位置，直接更新即可。
开 long long，ans 初始值要足够大。复杂度 O（nlogn)

#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
#define ll long long

int n,k,st,ed,q[100001];
ll dp[100001],a[100001],ans,tot;

ll read()
{
    ll x=0,f=1;char ch=getchar();
    while(ch<'0' || ch>'9') {if(ch=='-') f=-1;ch=getchar();}
    while(ch>='0' && ch<='9') {x=(x<<1)+(x<<3)+ch-'0';ch=getchar();}
    return x*f;
}

int main()
{
    n=read();k=read();ans=99999999999999999ll;
    for(int i=1;i<=n;i++) a[i]=read(),tot+=a[i];
    for(int i=1;i<=n;i++)
    {
        dp[i]=a[i]+dp[q[st]];
        while(st<=ed && dp[q[ed]]>dp[i]) ed--;q[++ed]=i;
        while(q[st]<i-k) st++;
    }
    for(int i=n-k;i<=n;i++) ans=min(ans,dp[i]);
    printf("%lld\n",tot-ans);
    return 0;
}

D题C++

E-这是一个数学题

链接：https://www.nowcoder.net/acm/contest/78/E
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

已知有一个n+1个数的数列,对于给定的A_0和A_n ，当i满足当1<=i<=n-1时有

现在小星想知道对于这个数列一段区间的和。

输入描述:

第一行输入四个数 n,A

₀

,An,Q

接下来Q行每行输入两个数l,r

0=< n,A₀,An<=1e9,Q<=100000

0<=l<=r<=n

输出描述:

对于每组查询输出A到Ar的和

示例1

输入

3 0 3 2
1 1
1 3

输出

1
6

备注:

为了对萌新表现出友好，数据保证了对于Ai的每一项都是整数

考察内容：简单数学公式。

题解：考虑将两边组合数化简于是得到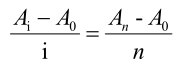

熟悉的同学应该能一眼发现 Ai 是个等差数列，公差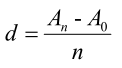

接下来查询就是一个等差数列求和，运用等差数列求和公式即可复杂度 O(1)
由于这题没有设置取模，所以在乘的时候要小心爆。
事实上这个结论可以加强为Ai 是等差数列的充要条件是：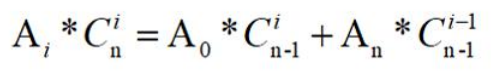

#include<bits/stdc++.h>
#define cl(a,b) memset(a,b,sizeof(a))
#define debug(a) cerr<<#a<<"=="<<a<<endl
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;

const int maxn=1e5+10;

int n,a0,an,q,p;

void query(int l,int r)
{

    ll al=a0+1ll*p*l;
    ll ar=a0+1ll*p*r;
    ll sum=(al+ar)*(r-l+1)/2;
    printf("%lld\n",sum);
}

int main()
{
    while(~scanf("%d%d%d%d",&n,&a0,&an,&q))
    {
        p=(an-a0)/n;
        int l,r;
        while(q--)
        {
            scanf("%d%d",&l,&r);
            query(l,r);
        }
    }
    return 0;
}

E题C++

F-大佬的生日礼包

链接：https://www.nowcoder.net/acm/contest/78/F
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

今天是某不愿透露姓名的谈姓大佬的生日，转发这场比赛到三个群就可以，获得以下三种礼包之一。

豪华礼包：一个U盘、一个鼠标和一个机械键盘。

幸运礼包：一个U盘、两个鼠标。

普通礼包：两个U盘、一个鼠标。

大佬一共准备了a个U盘、b个鼠标和c个机械键盘。为了给更多的人带来足够多的惊喜，大佬希望相邻的两位领礼包的参赛选手拿到的礼包类型都是不同的。

由于大佬正在宴请Final选手，并没有空打理这些，所以想让你告诉他这些奖品最多可以发出多少份礼包。

输入描述:

输入第一行包含一个正整数T。
接下来T行每行包含3个正整数a, b, c，依次表示U盘、鼠标和机械键盘各有多少个。

输出描述:

输出T行，每行一个整数，表示最多能发出多少份礼包。

示例1

输入

2
4 4 0
1 1 1

输出

2
1

备注:

T<=100000
0<=a,b,c<=1000000

考察内容：贪心，分类讨论，二分。

题解：首先观察题目可知，一共 1e5 个查询，这需要我们在 O(1)或者 O（logn）级别计算出结果。

解法一：由于礼包只有三种，显然答案和 a,b,c 存在这公式的关系，所以分类讨论几种情况即可。
解法二：我们发现只有豪华礼包才有键盘，而豪华礼包只需要 1 个 U 盘和 1 个鼠标。所以我们可以通过二分答案或者二分豪华礼包的方法来得到答案。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int T,a,b,c,s,t,ans,x,y,a1,b1,c1,ans1;
    scanf("%d",&T);
    while (T--)
    {
        scanf("%d%d%d",&a,&b,&c);
        if (a<c) c=a;
        if (b<c) c=b;
        if (a<b)
        {
            t=a;
            a=b;
            b=t;
        }
        a1=a;b1=b;c1=c;
        t=a-b;
        ans1=0;ans=0;
        if (c<=t)
        {
            x=(c-1)*2+c;
            y=c-1+c;
            if (x<=a&&y<=b)
            {
                ans=c+c-1;
                a-=x;b-=y;
                x=min(a/3,b/3);
                ans+=x*2;
                a-=x*3;b-=x*3;
                if (a>=2&&b>=1) ans++;
            }
            else
            {
                x=min(a/3,b/2);
                a-=x*3;b-=x*2;
                ans=x*2;
                if (a>=1&&b>=1) ans++;
            }
        }
        else
        {
            x=t*2+t;
            y=t+t;
            if (x<=a&&y<=b)
            {
                ans=t+t;
                a-=x;b-=y;
                c-=t;
                x=min(a/5,b/5);
                x=min(x,c/2);
                ans+=x*4;
                a-=x*5;b-=x*5;c-=x*2;
                if (a>=1&&b>=1&&c>=1)
                {
                    a--;b--;c--;
                    ans++;
                }
                x=min(a/3,b/3);
                ans+=x;
                a-=x*3;b-=x*3;
                if (a>=2&&b>=1) ans++;
            }
            else
            {
                x=min(a/3,b/2);
                a-=x*3;b-=x*2;
                ans=x*2;
                if (a>=1&&b>=1) ans++;
            }
        }
        ans1=ans;ans=0;
        a=a1;b=b1;c=c1;t=a-b;
        if (t>=c)
        {
            x=c*2+c;
            y=c+c;
            if (x<=a&&y<=b)
            {
                ans=c+c;
                a-=x;b-=y;
                x=min(a/3,b/3);
                ans+=x*2;
                a-=x*3;b-=x*3;
                if (a>=2&&b>=1) ans++;
            }
            else
            {
                x=min(a/3,b/2);
                a-=x*3;b-=x*2;
                ans=x*2;
                if (a>=2&&b>=1) ans++;
            }
        }
        else
        {
            x=t*2+t;
            y=t+t;
            if (x<=a&&y<=b)
            {
                ans=t+t;
                a-=x;b-=y;
                c-=t;
                x=min(a/5,b/5);
                x=min(x,c/2);
                ans+=x*4;
                a-=x*5;b-=x*5;c-=x*2;
                if (a>=3&&b>=2&&c>=1)
                {
                    a-=3;b-=2;c--;
                    ans+=2;
                }
                x=min(a/3,b/3);
                ans+=x*2;
                a-=x*3;b-=x*3;
                if (a>=1&&b>=2) ans++;
            }
            else
            {
                x=min(a/3,b/2);
                a-=x*3;b-=x*2;
                ans=x*2;
                if (a>=2&&b>=1) ans++;
            }
        }
        ans=max(ans,ans1);
        a=a1;b=b1;c=c1;
        if (c==0)
        {
            x=min(a/3,b/3);
            ans=x*2;
            a-=x*3;b-=x*3;
            if (a>=2&&b>=1) ans++;
        }
        printf("%d\n",ans);
    }
}

F题C++分类讨论-复杂度O（1）

#include<bits/stdc++.h>
using namespace std;

#define LL long long
#define LD long double
#define For(i,j,k) for (int i=j;i<=k;++i)
#define foR(i,j,k) for (int i=j;i>=k;--i)
#define mem(a,x) memset(a,x,sizeof(a))
#define sqr(x) (x)*(x)
template <typename T>void cmin(T &a,T b){a=min(a,b);}
template <typename T>void cmax(T &a,T b){a=max(a,b);}
template <typename T>
void read(T &x){
    char c;T f=1;
    while (!isdigit(c=getchar())) if (c=='-') f=-1;
    x=c-'0';
    while (isdigit(c=getchar())) x=x*10+c-'0';
    x*=f;
}
int main(){
    freopen("store.in","r",stdin);
    freopen("store.out","w",stdout);
    int T;
    read(T);
    For (i,1,T){
        int a,b,c;read(a),read(b),read(c);
        int l=0,r=0x7fffffff;
        while (l+1<r){
            int mid=(l+r)>>1,A=a-mid,B=b-mid,C=c;
            if (A>=0&&B>=0&&A+B+C>=mid&&(A+B)>=mid>>1&&(B+C)>=mid>>1&&(A+C)>=mid>>1)
                l=mid;
                else r=mid;
        } 
        printf("%d\n",l); 
    }
    return 0;
}

F题C++二分答案-复杂度O（logn）

G-零下e度

链接：https://www.nowcoder.net/acm/contest/78/G
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

在家好冷!

又多冷呢？

大概是零下e度!

为什么是零下e度呢?

不知道，因为我编不下去了。

求给定一个数n，求出最接近n!/e的整数

输入描述:

一行一个整数n
1<=n<=10^8

输出描述:

一行一个整数，即题目描述中所求，由于这个数字可能很大，我们只需要知道mod 998244353后的结果（出题人负责任地告诉你，这个数字是个质数）

示例1

输入

输出

示例2

输入

输出

158005593

示例3

输入

16777216

输出

16065816

考察内容：组合数学递推。

题解：我们将 n!/e 分成两部分 n!的意义是 n 个数的全排列，由于 1/e = e^(-1) = 1/0! - 1/1! + 1/2! - ..... + (-1)^n/n! + Rn(-1)，其中 Rn(-1)是余项，等于(-1)^(n+1) * e^u / (n+1)!，且 u∈(-1, 0)。
相乘就是一个错排公式 D(n) = n! (1/0! - 1/1! + 1/2! - 1/3! - ..... +(-1)^n/n!)，所以，D(n) = n! * e^(-1) - (-1)^(n+1) * e^u / (n+1), u∈(-1, 0).。而|n! Rn| = |(-1)^(n+1) * e^u / (n+1)| = e^u / (n+1) ∈ (1/[e(n+1)]，1/(n+1))，可知即使在 n=1 时，该余项（的绝对值）也小于 1/2。
因此，无论 n! Rn 是正是负，n! / e + 1/2 的整数部分都一定与 M(n)相同。所以这题就变成了求 n 位数的错排。
对于 n<=1e8 的单组查询，我们有递推式D(n) = (n-1) [D(n-2) + D(n-1)]
显然不能用数组存，维护三个变量更新即可。
注意取模的常数较大尽量减少取模。

#include<bits/stdc++.h>
using namespace std;
int main()
{
    int n,i,j,k,f;
    long long x,y,q=998244353,ans,s;
    scanf("%d",&n);
    if (n==1) ans=0;
    if (n==2) ans=1;
    x=0;
    y=1;
    for (i=3;i<=n;i++)
    {
        s=(x+y)*(i-1)%q;
        x=y;
        y=s;
    }
    if (n>2) ans=y;
    cout<<ans<<endl;
}

G题C++-复杂度O（N）

H-酸碱滴定

链接：https://www.nowcoder.net/acm/contest/78/H
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

有时候你会抱怨，什么时候才能到终点。

有时候你会迫不及待，怎么颜色还不改变。

滴定管长场的，我们的路长长的。

用心的放入每一滴，终点就在你手心。

今天小星需要去完成一个酸碱滴定实验。，实验室老师要求用 A mol/L 的HCL去测定一瓶NaOH的浓度。首先小星取出了一个锥形瓶，在里面放入的Bml的NaOH，并滴加1-2滴甲基橙，然后用HCL去滴定他当滴定至恰好变为红色时（可以认为H离子浓度等于OH离子浓度），用了C ml

小星现在需要计算NaOH的浓度是多少？单位（mol/L）

对于浓度采用化学里“四舍六入五成双”方法保留2位小数

规则1 ：第三位小数≤4 时舍去

规则2：第三位小数≥6时进上

规则3：第三位小数等于5时

3.1首先根据 5后面的数字来定，当5后有数时，舍5入1；

3.2当5后无有效数字时，需要分两种情况来讲：

3.2.1 5前为奇数，舍5入1；

3.2.2 5前为偶数，舍5不进（0是偶数）

例如

9.8249=9.82 规则1

9.82671=9.83 规则2

9.82501=9.83 规则3.1

9.8351 =9.84 规则3.1

9.8350=9.84 规则3.2.1

9.8250=9.82 规则3.2.2

输入描述:

输入第一行一个数T(T<=20)表示数据组数
对于每组数据输入 A,B,C三个3位小数
0.000<a,b,c<50.000

输出描述:

结果“四舍六入五成双”保留2位小数

示例1

输入

3
10.000 10.000 1.825
10.000 10.000 9.835
1.010 21.325 19.823

输出

1.82
9.84
0.94

说明

样例1中计算出的结果为 1.8250000000根据(规则3.2.2) 答案应该为1.82
9.835->9.84(规则3.2.1)

考察内容：细节处理。
题解：答案就是 a*c/b，然后根据规则分类讨论下就好，注意进位。

#include <bits/stdc++.h>
using namespace std;

void solve(){
    double a, b, c;
    cin >> a >> b >> c;
    double ans = (a * c )* 100.0 / b;
    if( ans-(int)ans < 0.499 ) ans = (int)ans / 100.0;
    else if ( ans-(int)ans >0.501 ) ans = ((int)ans+1) / 100.0;
    else{
        if( ((int)ans)%2 ) ans = ((int)ans+1) / 100.0;
        else ans = (int)ans / 100.0;
    }
    printf("%.2lf\n", ans);
    return;
}

int main(){
    int n;
    cin >> n;
    while(n--){
        solve();
    }
    return 0;
}

H题C++

I-合成反应

链接：https://www.nowcoder.net/acm/contest/78/I
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld

题目描述

有机合成是指从较简单的化合物或单质经化学反应合成有机物的过程。

有时也包括从复杂原料降解为较简单化合物的过程。

由于有机化合物的各种特点，尤其是碳与碳之间以共价键相连，有机合成比较困难，常常要用加热、光照、加催化剂、加有机溶剂甚至加压等反应条件。

但是前人为有机合成提供了许多宝贵的经验。

现在已知有K总物质和N个前人已经总结出的合成反应方程式

小星想知道在现有M种物质的情况下能否合成某些物质。

输入描述:

第一行输入四个整数 K,N,M,Q（K,N,M,Q<=1e5）
K表示一共K总物质
接下来N行 每行三个数字a b c（任意两个数可能相等）
表示a和b反应可以生成c 反应是可逆的
即可以通过c可以分解出a和b
接下来一行行然后输入m个数，表示m种原料（每一种原料都可以认为有无限多）
接下来Q个行Q个询问
对于每个询问
输出一个数字 x 判断是否可以通过一些反应得到第 x

输出描述:

可以得到Yes否则No

示例1

输入

输出

Yes
Yes
Yes
Yes
Yes
Yes
Yes
Yes
No
No

说明

一共10总物质有第3，4，5，8 四种原料
查询每一种是否可以通过反应得到
首先通过3可以分解得到1 2
然后4 5合成6
2 5合成7
于是除了9 10都可以得到

考察内容：bfs 暴力剪枝
题解：这道题灵感来源是有机化学中的合成题。
解法一：
首先的一个最简单想法是每次对所以配方做一次分解，一次合成，然后做到无法做很不幸这样的做法被出题人卡掉了，但是我们可以尝试剪枝剪过去。
每次优先考虑分解，一旦发现合成新的物质就先去分解，然后检查一下能否合成这两步无限循环，发现无法合成就跳出，这样复杂的是均摊 O（logn）级别的，出题人水平有限卡不掉。

解法二：
标程的做法是 bfs
我们考这样一个有向图对于每个配方建四条边
c->b 权值为 a ，
c->a 权值为 b
a->c 和 b->c 权值为-1
比如输入的配方是（a, b），能合成 c
然后建四条边
c->b 权值为-1
c->a 权值为-1
a->c 权值为 b
b->c 权值为 a
然后做一次 bfs 首先把原料都丢进去队列,然后每次到一个点访问它的后继如果它和它的权值都是有的那么就丢进去。
例如节点 x 能到节点 y 的条件是他们之间的有向边的权值 z 是-1 或者 zx 存在原料库当中的这样复杂度大概是 O(N+M)。

#include<bits/stdc++.h>
using namespace std;
struct sam
{
    int x,y,z;
};
int n,i,j,k,s,t,m,q,top,tail,f;
sam a[100010];
int b[100010],c[200010],d[100010][3];
int cmp(sam &p,sam &q)
{
    return (p.z<q.z);
}
int work(int t)
{
    int ans;
    if (d[t][1]==0&&d[t][2]==0) return 0;
    ans=d[t][1];
    while (ans<=d[t][2])
    {
        if (b[a[ans].x]==0)
        {
            b[a[ans].x]=1;
            top++;
            c[top]=a[ans].x;
        }
        if (b[a[ans].y]==0)
        {
            b[a[ans].y]=1;
            top++;
            c[top]=a[ans].y;
        }
        ans++;
    }
    return 1;
 //   b[t]=2;
}
int main()
{
    scanf("%d%d%d%d",&k,&n,&m,&q);
    for (i=1;i<=n;i++)
    {
        scanf("%d%d%d",&a[i].x,&a[i].y,&a[i].z);
    }
    sort(a+1,a+1+n,cmp);
    memset(d,0,sizeof d);
    for (i=1;i<=n;i++)
    {
        t=a[i].z;
        if (d[t][1]==0) d[t][1]=i;
        d[t][2]=i;
    }
    tail=1;top=0;
    for (i=1;i<=m;i++)
    {
        scanf("%d",&t);
        if (b[t]==0)
        {
            b[t]=1;
            top++;
            c[top]=t;
        }
    }
    while (tail<=top)
    {
        work(c[tail]);
        tail++;
    }
    f=0;
    while (f==0)
    {
        f=1;
        for (i=1;i<=n;i++)
            if (b[a[i].x]>0&&b[a[i].y]>0&&b[a[i].z]==0)
        {
            f=0;
            b[a[i].z]=1;
            top++;
            c[top]=a[i].z;
            while (tail<=top)
            {
                work(c[tail]);
                tail++;
            }
        }
        if (f==1) break;
        f=1;
        for (i=n;i>=1;i--)
            if (b[a[i].x]>0&&b[a[i].y]>0&&b[a[i].z]==0)
        {
            f=0;
            b[a[i].z]=1;
            top++;
            c[top]=a[i].z;
            while (tail<=top)
            {
                work(c[tail]);
                tail++;
            }
        }
    }
    for (i=1;i<=q;i++)
    {
        scanf("%d",&t);
        if (b[t]==0) printf("No\n"); else printf("Yes\n");
    }
}

I题C++解法一

#include<bits/stdc++.h>
using namespace std;
int a[100010];
struct hxfy
{
    int x,y,z;
} b[100010];
int c[100010];
struct node
{
    int x,v;
};
vector<node> v[100010];
queue<int> Q;
int vis[100010];
void bfs()
{
    while(!Q.empty())
    {
        int f=Q.front();
      //  cout<<f<<endl;
        Q.pop();
        for(int i=0; i<v[f].size(); i++)
        {
            
            if(v[f][i].v==-1)
            {
                if(vis[v[f][i].x]==0)
                {
                    a[v[f][i].x]=1;
                    Q.push(v[f][i].x);
                    vis[v[f][i].x]=1;
                }
            }
            else
            {
                if(a[v[f][i].v])
                {
                    if(vis[v[f][i].x]==0)
                    {
                        Q.push(v[f][i].x);
                        vis[v[f][i].x]=1;
                         a[v[f][i].x]=1;
                    }

                }
            }
        }
    }

}
int main()
{
  //freopen("1","r",stdin);
  // freopen("2","w",stdout);
    int k,n,m,q;
    scanf("%d%d%d%d",&k,&n,&m,&q);
    for(int i=1; i<=n; i++)
    {
        int x,y,z;
        scanf("%d%d%d",&x,&y,&z);
        b[i].x=x;
        b[i].y=y;
        b[i].z=z;
        v[x].push_back((node)
        {
            z,y
        });
        v[y].push_back((node)
        {
            z,x
        });
        v[z].push_back((node)
        {
            y,-1
        });
        v[z].push_back((node)
        {
            x,-1
        });

    }
    memset(a,0,sizeof(a));
    memset(c,0,sizeof(c));
    memset(vis,0,sizeof(vis));
    for(int i=1; i<=n; i++)
    {
        c[b[i].z]=i;
    }
    for(int i=1; i<=m; i++)
    {
        int x;
        scanf("%d",&x);
        a[x]=1;
        Q.push(x);
    }
    bfs();
    for(int i=1; i<=q; i++)
    {
        int x;
        scanf("%d",&x);
        if(a[x])
            printf("Yes\n");
        else
            printf("No\n");
    }
}

I题C++解法二

J-同分异构体

链接：https://www.nowcoder.net/acm/contest/78/J
来源：牛客网

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述

化学上，同分异构体是一种有相同分子式而有不同的原子排列的化合物。简单地说，化合物具有相同分子式，但具有不同结构的现象，叫做同分异构现象；

输入一个数n，求n个碳的烷烃（仅由碳、氢、碳碳单键与碳氢单键所构成）的同分异构体的数目n=3,4,5如下图所示

输入描述:

输入一个数n(n<=9)

输出描述:

一个整数表示答案

示例1

输入

输出

示例2

输入

输出

示例3

输入

输出

备注:

这里不考虑空间异构

考察内容：打表。

#include<bits/stdc++.h>
using namespace std;
int a[11]={1,1,1,2,3,5,9,18,35};
int main()
{
    int n;
   cin>>n;
   cout<<a[n-1]<<endl;

}

J题C++

posted @ 2018-02-08 18:11 Zoctopus_Zhang 阅读(559) 评论(0) 编辑收藏举报

刷新页面返回顶部

~不会飞的章鱼~

孰能生巧，勤能补拙，念念不忘，必有回响！

牛客网平台常州大学新生寒假训练会试

A-添加逗号

题目描述

输入描述:

输出描述:

输入

输出

备注:

B-对称

题目描述

输入描述:

输出描述:

输入

输出

输入

输出

说明

备注:

C-竞赛技巧

题目描述

输入描述:

输出描述:

输入

输出

说明

D-训练技巧

题目描述

输入描述:

输出描述:

输入

输出

说明

备注:

E-这是一个数学题

题目描述

输入描述:

输出描述:

输入

输出

备注:

F-大佬的生日礼包

题目描述

输入描述:

输出描述:

输入

输出

备注:

G-零下e度

题目描述

输入描述:

输出描述:

输入

输出

输入

输出

输入

输出

H-酸碱滴定

题目描述

输入描述:

输出描述:

输入

输出

说明

I-合成反应

题目描述

输入描述:

输出描述:

输入

输出

说明

J-同分异构体

题目描述

输入描述:

输出描述:

输入

输出

输入