Luhn算法检验和验证

一、Luhn公式介绍

Luhn公式是一种广泛使用的系统，用于对标识号进行验证。它根据原始标识号，把每隔一个数字的值扩大一倍。然后把各个单独数字的值加在一起（如果扩大一倍后的值为2个数字，就把这两个数字分别相加）。如果相加之后可以被10整除，那么这个标识号就是合法的。

编写一个程序，接受一个任意长度的标识号，并根据Luhn公式确定这个标识号是否合法。这个程序在读取下一个字符之前必须处理之前所读取的那个字符。

过程有些复杂，在此上传一张图片以供各位理解：

 记住：最终标识号的检验和应该能够被10整除，或者说应该以0结尾。

 

二、问题分步求解

1. 知道哪些数字需要扩大一倍。
2. 对扩大一倍后大于等于10的数字，根据他们的单独数字进行处理。
3. 知道已经到达了标识号的尾部。
4. 分别读取每个数字。

（注：我们不需要按照特定的顺序处理这些问题。）

 

首先，我们处理扩大一倍后大于或等于10的数：

如果我们从单独的数字0~9开始并把它们扩大一倍，最大值将是18。因此，一共只有两种可能性：如果扩大一倍后的值为单个数字，就不需要再做处理；如果扩大一倍后的值大于或等于10，它的范围肯定在10~18之间，因此第一个数字总是为1.我们通过一个代码来验证一下：

    int digit;
    printf("Enter a single digit number,0-9:");
    scanf("%d",&digit);
    int doubledDigit = digit * 2;  //程序读取数字，并把它的值扩大一倍 
    int sum;
    if(doubledDigit >= 10)
        sum = 1 + doubledDigit % 10;  //求和计算 
    else
        sum = doubledDigit;
    printf("Sum of digits in doubled number:%d\n",sum);  //输出求和结果 

验证结果如下：

我们可以把这段代码转化为一个短小的函数，这样就可以简化未来的代码了。（是不是很有远见呢？）

int doubleDigitValue(int digit)
{
    int doubledDigit = digit * 2;  //程序读取数字，并把它的值扩大一倍 
    int sum;
    if(doubledDigit >= 10)
        sum = 1 + doubledDigit % 10;  //求和计算 
    else
        sum = doubledDigit;
    return sum;
}

 

现在，我们读取标识号的单独数字：

如果我们以数值类型（例如int）的形式读取标识号，将会读取一个长长的数，需要处理很多事情。另外，可以读取的最大整数也是有限制的。但在该问题中，标识号可以是任意长度的。因此，我们必须逐字符读取。这意味着我们要知道怎样读取一个表示数字的字符并把它转换为整数类型，以便对它进行数学运算。来看以下代码：

    char digit;
    printf("Enter a one-digit number:");
    scanf("%c",&digit);
    int sum = digit;
    printf("Is the sum of digits:%d?\n",sum); 

运行结果为：

字符7是以字符码值55存储的，因此当我们把这个字符作为整数时，得到的结果就是55.

因此，我们需要一种机制把字符7转换为整数7。

我们可以创建一张表，其中包含原值和目标值，还有两值之间的误差。

字符码-目标整数值

字符	字符码	目标整数值	差
0	48	0	48
1	49	1	48
2	50	2	48
3	51	3	48
4	52	4	48
5	53	5	48
6	54	6	48
7	55	7	48
8	56	8	48
9	57	9	48

字符码和目标整数值之差始终是48，因此我们需要做的就是使字符码减去这个值。而48正好是0的字符码，所以我们可以采用一种更通用、更容易理解的解决方案：就是减去字符0的字符码而不是减去像48这样预先确定的值：

    char digit;
    printf("Enter a one-digit number:");
    scanf("%c",&digit);
    int sum = digit - '0';
    printf("Is the sum of digits:%d?\n",sum); 

运行结果为：

 

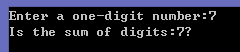
现在，我们转到问题的下一部分，判断哪些数字需要扩大一倍：

我们可以先试着把长度限制为6，则我们只需要读取6个数字，对它们进行求和，然后判断它们的和是否被10所整除，代码如下：

    char digit;
    int checksum = 0;
    printf("Enter a six-digit number:");
    for(int position = 1;position <= 6;position++){
        scanf("%c",&digit);
        checksum += digit - '0';
    }
    printf("Checksum is:%d\n",checksum);
    if(checksum%10 == 0)
        printf("Valid:Checknum is divisible by 10\n"); 
    else
        printf("Invalid:Checknum is not divisible by 10\n");

运行结果为：

  

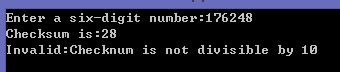
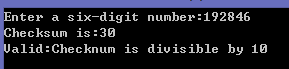
现在，我们需要为实际的Luhn检验公式增加逻辑，把从左边开始位置为奇数的数字扩大一倍。我们可以使用求摸操作符（%）确定奇数和偶数的位置，因为偶数的定义是它能够被2所整除。因此如果表达式位置%2的结果是1，这个位置就是奇数，应该把它扩大一倍。顺便插一句，在扩大一倍后，如果结果大于或等于10，还需要对这个结果的各个数字进行求和。代码如下（只需把for循环那改一下）：

    for(int position = 1;position <= 6;position++){
        scanf("%c",&digit);
        if(position%2 == 0) checksum += digit - '0';
        else checksum += doubleDigitValue(digit - '0');
    }

运行结果为：

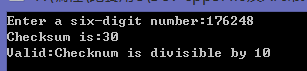
到目前为止，我们在这个问题上已经取得很大的进展，但还需要完成一些步骤才能为任意长度的标识号编写代码。为了最终解决这个问题，我们需要采用分治法。

先考虑怎样处理长度为任意偶数的标识号。

我们所面临的第一个问题是怎样确定已经到达了标识号的末尾。如果用户输入了一个多位的标识号又按下了Enter键表示结束，并且我们是逐个字符读取输入的，那么在最后一个数字之后所读取的字符是什么呢？我们不妨用代码来试验一下：

    printf("Enter a number:");
    char digit;
    while(1){
        scanf("%c",&digit);
        printf("%d\n",int(digit));
    }

运行结果为：

  

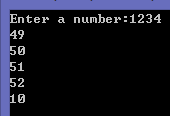
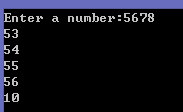
输入1234，结果是49 50 51 52 10（结果基于ASCII码）。从运行结果中可以看出，10就是我们所寻找的结果，所以我们可以在前面的代码中用一个while循环代替for循环：

    //处理任意偶数长度的标识号 
    char digit;
    int checksum = 0;
    int position = 1;
    printf("Enter a number with an even number of digits:");
    scanf("%c",&digit);  //读取第一个值 
    while(digit != 10){  //用来检查字符码的值是否为行末符 
        if(position%2 == 0)  //偶数位判断 
         checksum += digit - '0';
        else checksum += 2 * (digit - '0');
        scanf("%c",&digit);  //读取每个后续的值 
        position++;
    }
    printf("Checksum is:%d\n",checksum);
    if(checksum%10 == 0)
        printf("Valid:Checksum is divisible by 10\n");
    else
        printf("Invalid:Checksum is not divisible by 10\n");

运行结果为：

 

现在已经解决了“怎样确定已经到达了标识号的末尾”的问题。

要穷尽每种可能性，标识号的长度必须是奇数或者偶数。如果我们预先知道长度，就可以知道应该把奇数位的数字或者偶数位的数字扩大一倍。但是，在读取完这个标识号之前，我们并不知道这个信息。在思考这个问题前，我们先来类比另外一个问题：

编写一个程序，从用户那里读取10个整数。在输入了所有的整数之后，要求显示这些数中正数或负数的数量。

编写思路：需要一个对正数进行计数的变量，并用另一个变量对负数进行计数。当用户在程序的最后指定了具体的请求时，只需显示适当的变量作为响应即可。代码如下：

 

    int number;
    int positiveCount = 0;
    int negativeCount = 0;
    for(int i = 1;i <= 10;i++){
        scanf("%d",&number);
        if(number > 0) positiveCount++;  //计数正值 
        if(number < 0) negativeCount++;  //计数负值 
    } 
    char response;  //选择回答 
    printf("Do you want the (p)ositive or (n)egative count?");
    getchar(); //吞掉回车 
    scanf("%c",&response);
    if(response == 'p')
     printf("Positive Count is %d\n",positiveCount);
    if(response == 'n')
     printf("Negative Count is %d\n",negativeCount);

运行结果为：

  

这个类比的问题显示了我们在解决Luhn检验和问题时所需要用到的方法：同时以两种方式追踪当前的检验和，分别是在标识符为奇数长度和偶数长度的情况下。当我们读取完这个编号并确定了它的真正长度时，再选择表示正确的检验和的变量。

现在，我们可以把所有的代码都集中在一起，来解决这个问题了。

 

三、完整代码

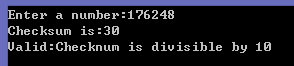
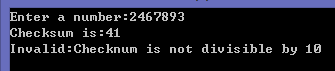
    char digit;
    int oddLengthChecksum = 0;
    int evenLengthChecksum = 0;
    int position = 1;
    printf("Enter a number:");
    scanf("%c",&digit);
    while(digit != 10){
        if(position%2 == 0){
            oddLengthChecksum += doubleDigitValue(digit - '0');
            evenLengthChecksum += digit - '0';
        }
        else{
            oddLengthChecksum += digit - '0';
            evenLengthChecksum += doubleDigitValue(digit - '0');
        }
        scanf("%c",&digit);
        position++;
    }
    int checksum;
    if((position - 1)%2 == 0) checksum = evenLengthChecksum;
    else checksum = oddLengthChecksum;
    printf("Checksum is:%d\n",checksum);
    if(checksum%10 == 0)
        printf("Valid:Checknum is divisible by 10\n"); 
    else
        printf("Invalid:Checknum is not divisible by 10\n");

运行结果为：

   

 

感受

这篇博文写了一晚上，视力开始模糊了，而且还有一些头痛的症状，可能是昨天下午出去玩吹凉风了。不过今天还是很开心的，看着一个完整的算法被我们切成一小块一小块的细致分析和代码检验，沉浸于其中，一点点的接近真相，我感到兴奋和快乐！刚开始我还对函数调用和程序中的回车问题有所疑惑，不过在一位朋友的指点下我还是顺利通过了。最重要的是，我对这个算法也有了更深一步的了解与认识。