从编译原理看一个解释器的实现
『设计模式』中有一个模式可以解释特定的语法规则,它就是解释器模式(Interpreter Pattern)。不同于常见的策略模式或者是工厂模式,解释器模式在.NET或者JDK中并不常见,而且在业务上也很少会去解释特定的语法,所以它并不被广泛使用。一个解释器可大可小,大可以是复杂的编译器,小也可以是一个简单的字符串解析,但本质上它们都是对特定的语法做出合理的解释。
解释器在游戏领域的应用
虽然解释器模式很少使用,但在在游戏开发中,还是很常见的。比如你在战斗时,普通攻击和魔法攻击一定会产生不同的伤害,游戏设计者会为技能设计不同的『公式』,简单如我方的攻击力-敌方的防御力,同时『公式』还可以加入参数,如$critRate代表一个爆发率。故游戏的技能伤害如下图所示:
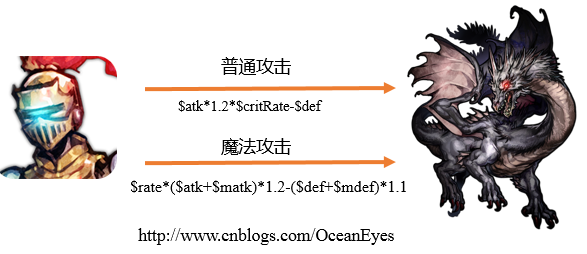
游戏里的『公式』本质上是字符串,很像数学表达式,但又比它更高级,可以加入自定义的参数,所以『公式』更像是数学表达式的超集。既然谈到了数学表达式,那么有必要知道怎样去解析一个数学表达式。
千万不要小看这个任务,实际上要做一个计算器是非常复杂的。假设输入一个字符串:-(1+(2+3)x4-5),注意这是一个字符串。解决方案有两种:
while遍历字符串,将括号、运算符、数字等取出来,根据运算符左结合以及优先级计算- 将表达式转化成二叉树形式,二叉树的父节点是运算符,左右子节点代表数字,通过递归遍历树,将左右节点的数字运算之后放入父节点,直至到达根节点
很显然第一种方式简单直白,但很繁重,代码的易读性也不佳,第二种是目前最好的解决方式,将表达式转化为二叉树。所以难点在于怎样将表达式转化为一棵二叉树?
这需要了解数据结构相关知识,表达式-(1+(2+3)x4-5)又被称为中序排序,中序排序不能生成一棵二叉树,你需要将中序排序转化为前序排序或者后序排序,然后根据中序排序和前序排序生成二叉树,相关算法自行搜索,不做累赘。
我在阅读了《编译原理》第1,2章之后,还有另外一种方式将表达式生成二叉树形式,这也是编译的基本原理。
一个编译器的前端模型###
我们以最简单的算术表达式举例,编译器在分析阶段把一个字符序列分为各个组成部分,最终生成一棵抽象语法树(abstract syntax tree),如下所示:
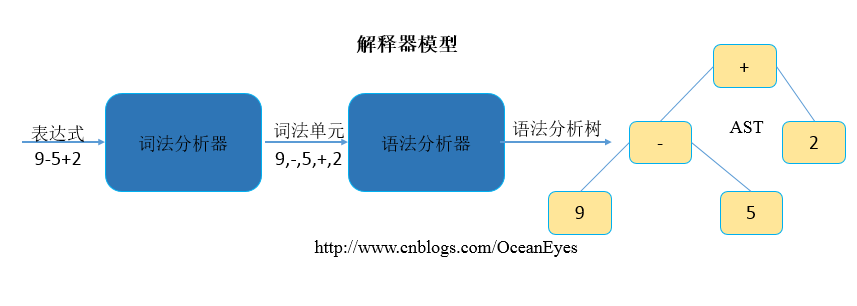
表达式语法定义
语法,顾名思义,是一种特定的描述方法。我们学习的英语语法,又或者是程序语言的语法,都有严格的格式要求。对于算术表达式而言,比如9-5+2,3-2,语法是两个数字之间必须出现+,-,如果出现9+-5,那么这就是错误的语法。
那我们怎么来制定语法呢?在编译原理领域,使用一个通用的表示方法来描述语法,这个方法就是上下文无关文法或BNF范式。
比如上述的算术(+和-)表达式:9-5+2,我们可以推导出如下BNF范式:
list->list+digit|list-digit|digit
digit->0|1|2|3|4|5|6|7|8|9
list代表一个表达式序列,digit代表数字,箭头->可以读作“可以具有如下形式”,而竖线|代表或的意思。
词法分析器
词法分析器读入源程序中的字符序列,将他们组织为具有词法含义的词素,生成并输出代表这些词素的词法单元(Token)。
语法分析器
语法分析器根据词法单元,以语法分析树的形式构建表达式,最终形成一颗抽象的语法树(abstract syntax tree),这是一种表示了层次化的结构。
语法分析树
如果非终端节点A有一个产生式A->XYZ,那么在语法分析树中就可能有一个标号为A的内部节点,该节点有三个子节点,从左向右标号为X,Y,Z。内部节点对应于产生式的头,它的子节点对应于产生式的体:
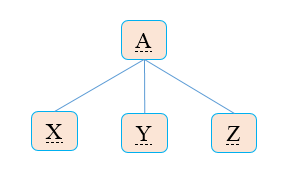
BNF范式构建###
数学表达式的特点
运用编译原理的知识,编写一个自定义的解释器,我们需要如下三个步骤:
- BNF范式来描述游戏『公式』
- 词法分析器获得词法单元Token,对应的类是
LexicalAnalyzer - 语法分析器根据Token构建抽象树,对应的类是
Parser
我在一开始就提到过,游戏里的『公式』很像数学表达式,那么数学表达式有什么广泛和通用的特点?
首先数学表达式由数字和运算符构成,并且运算符有左结合性和优先性:
- 结合性:依照惯例,9+5+2等价于(9+5)+2,9-5-2等价于(9-5)-2。当一个运算分量,比如上述的5左右两侧都有运算符时,我们需要一些规则来决定哪个运算符被应用于该运算分量。我们说运算符“+”是左结合的,因为当一个运算分量左右两侧都有“+”号时,它属于其左边运算符。加,减,乘,除四种算术运算符都是左结合。
- 优先性:在算术中,乘法和除法比加法和减法具有更高的优先级。因此在表达式9+5x2和9x5+2中,都是运算分量5首先参与x运算。
算术表达式的BNF构建
通过对数学表达式的了解,我们知道一个数学表达式有数字、运算符等组成,并且运算符是左结合和有优先性,那怎样去构建它的BNF范式呢?
我们创建两个非终结符号expr(表达式) 和 term(项) ,分别对应这两个优先级层次,并使用另一个非终结符号factor(因子)来生成表达式的基本单元。
那什么是factor呢?
我们可以将因子(factor)理解成不能被任何运算符分开的表达式。『不能分开』的意思是说当我们在任意因子的任意一边放置一个运算符,都不会导致这个因子的任何部分分离出来,成为这个运算符的运算分量。当然,因子本身作为一个整体可以成为该运算符的一个运算分量。如果这个因子是由一个括号括起来的表达式,那么这个括号将起到保护其不被分开的作用。
factor->digit|(expr)
digit->0|1|2|3|4|5|6|7|8|9
那什么是term呢?
一个(不是因子)项(term)是一个可能被高优先级的运算符x和/分开,但不能被低优先级运算符分开的表达式。
term->term x factor|term / factor|factor
那什么是expr呢?
一个(不是因子也不是项)的表达式可能被任何一个运算符分开。
expr->expr+term|expr-term|term
因此最终得到的BNF范式是:
expr->expr+term|expr-term|term
term->term x factor|term/factor|factor
factor->digit|(expr)
使用这个BNF范式时,一个表达式就是一个由+或-分割开来的项(term)列表,而项是由x或者/分隔的因子(factor)列表。请注意,任何由括号括起来的表达式都是一个因子。
这个BNF范式的语法分析树为如下所示:
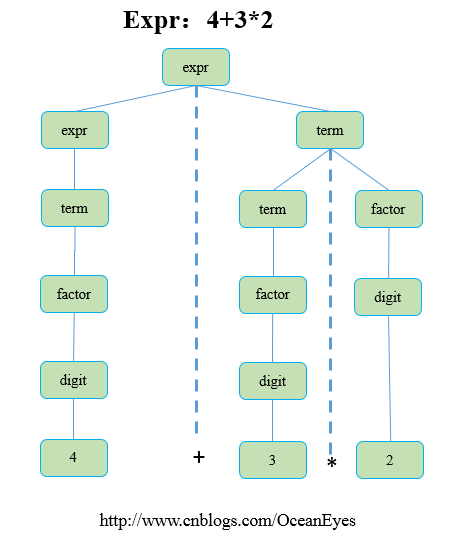
求值时,从root节点遍历二叉树,如果节点有子节点,递归的方式遍历下去,直到是叶子节点为止,接着将左子树和右子树取得的值放入它们的根节点,最后root节点的值就是表达式最终的值。
开始实现解释器###
有了准备之后,接下来就是实现解释器,它可以解释游戏中的『公式』。
1.) 创建一个数学表达式类MathExpression,根据面向对象思想,它封装了数据和行为,由于篇幅有限,只展示其骨架:
public class MathExpression
{
private readonly string _expression;
public int CurrentIndex{}
public bool IsIndexOutOfRange{}
public bool IsEndOfString{}
public char CurrentChar{}
public char GetSpecificCharByIndex(int index){}
}
2.) 创建一个词法分析器LexicalAnalyzer,获取对应的词法单元Token:
switch (_mathExpression.CurrentChar)
{
case '+':
token = Token.Add;
_mathExpression.CurrentIndex++;
break;
case '-':
token = Token.Sub;
_mathExpression.CurrentIndex++;
break;
case '*':
token=Token.Mul;
_mathExpression.CurrentIndex++;
break;
case '/':
token = Token.Div;
_mathExpression.CurrentIndex++;
break;
case '(':
token = Token.OParen;
_mathExpression.CurrentIndex++;
break;
case ')':
token = Token.CParen;
_mathExpression.CurrentIndex++;
break;
case '$':
if (_mathExpression.GetSpecificCharByIndex(_mathExpression.CurrentIndex + 1) =='c')
{
_mathExpression.CurrentIndex += 2;
token = Token.Param;
}
else
{
_mathExpression.CurrentIndex++;
token=Token.Illegal;
}
break;
default:
if (char.IsDigit(_mathExpression.CurrentChar))
{
token = GetDigitsFromString();
}else if (char.IsLetter(_mathExpression.CurrentChar))
{
token = GetSineCosineFromString();
}
else
{
throw new Exception("Illegal Token");
}
break;
}
3.) 值得一提的事情,怎样从字符串中获取数字,数字有两种形式:整数和小数点形式,通过有穷自动机在不同的状态间跳转并记录下数字的索引下标,直到遇到非数字退出,有穷自动机如下所示:
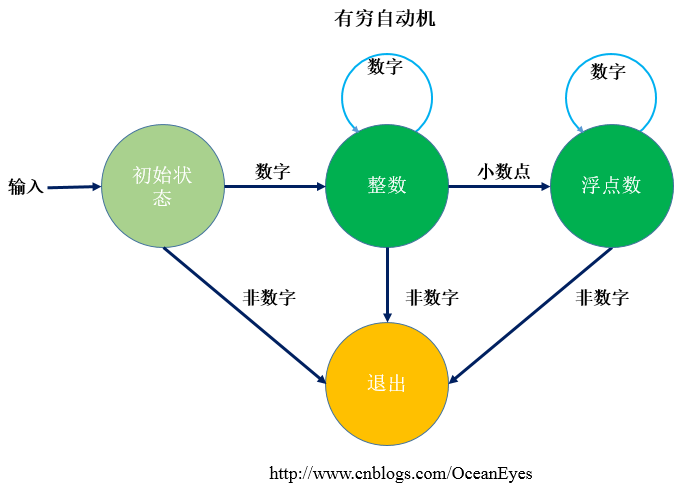
一个有穷自动机的状态判断代码如下:
do
{
isEndOfString = _mathExpression.IsEndOfString;
currentChar = _mathExpression.CurrentChar;
switch (_currentState)
{
case State.Init:
if (char.IsDigit(currentChar))
{
_currentState = State.Integer;
if (!isEndOfString)
{
_mathExpression.CurrentIndex++;
}
}
else
{
//Init状态非数字则退出
_currentState= State.Quit;
}
break;
case State.Integer:
if (currentChar == '.')
{
_currentState = State.Float;//输入小数点,状态转移到Float
if (!isEndOfString)
{
_mathExpression.CurrentIndex++;
}
}
else
{
if (!char.IsDigit(currentChar))//既不是数字也不是小数
{
_currentState = State.Quit;
}
else
{
if (!isEndOfString)
{
_mathExpression.CurrentIndex++;//读取下一个字符
}
}
}
break;
case State.Float:
if (!char.IsDigit(currentChar))//非数字,退出
{
_currentState = State.Quit;
}
else
{
if (!isEndOfString)
{
_mathExpression.CurrentIndex++;
}
}
break;
case State.Quit:
break;
}
} while (_currentState != State.Quit && !isEndOfString);
4.)通过语法解析器Parser构建表达式树,每个节点都是一个抽象Expression
public abstract class Expression
{
public abstract double Evaluate(Context context);
}
Expression根据类型不同有常量表达式,二元表达式,一元表达式等,一个常见的二元表达式如下:
public class BinaryExpression:Expression
{
private Expression _leftExpression;
private Expression _rightExpression;
private Operator _operator;
public BinaryExpression(Expression leftExpression,Expression righExpression,Operator op)
{
_leftExpression = leftExpression;
_rightExpression = righExpression;
_operator = op;
}
public override double Evaluate(Context context)
{
switch (_operator)
{
case Operator.Plus:
return _leftExpression.Evaluate(context) + _rightExpression.Evaluate(context);
case Operator.Minus:
return _leftExpression.Evaluate(context) - _rightExpression.Evaluate(context);
case Operator.Mul:
return _leftExpression.Evaluate(context) * _rightExpression.Evaluate(context);
case Operator.Div:
return _leftExpression.Evaluate(context) / _rightExpression.Evaluate(context);
}
return Double.NaN;
}
}
可以看到左子树和右子树同样是Expression。
5.)到目前为止,可以说是万事俱备,只欠东风了,这个『东风』就是怎么样去构建表达式树。已知的是,一个 expr 就是一个由+或-分割开来的项( term )列表,而项是由x或者/分隔的因子( factor )列表。
expr->expr+term|expr-term|term
private Expression Expr()
{
Token old;
Expression expression = Term();
while (_currentToken==Token.Add|| _currentToken==Token.Sub)
{
old = _currentToken;
_currentToken = _lexicalAnalyzer.GetToken();
Expression e1 = Expr();
expression=new BinaryExpression(expression,e1,old==Token.Add?Operator.Plus:Operator.Minus);
}
return expression;
}
term->term x factor|term/factor|factor
private Expression Term()
{
Token old;
Expression expression = Factor();
while (_currentToken==Token.Mul || _currentToken==Token.Div)
{
old = _currentToken;
_currentToken = _lexicalAnalyzer.GetToken();
Expression e1 = Term();
expression=new BinaryExpression(expression,e1,old==Token.Mul?Operator.Mul:Operator.Div);
}
return expression;
}
factor->digit|(expr)
private Expression Factor()
{
Token token;
Expression expression;
if (_currentToken==Token.Double)
{
expression=new NumericConstant(_lexicalAnalyzer.GetDigits());
_currentToken = _lexicalAnalyzer.GetToken();
}
else if (_currentToken == Token.Param)
{
expression=new Var();
_currentToken = _lexicalAnalyzer.GetToken();
}
else if (_currentToken==Token.OParen)
{
_currentToken = _lexicalAnalyzer.GetToken();
expression = Expr();
if (_currentToken!=Token.CParen)
{
throw new Exception("Missing Closing Parenthesis\n");
}
_currentToken = _lexicalAnalyzer.GetToken();
}
else if(_currentToken==Token.Add || _currentToken==Token.Sub)
{
var old = _currentToken;
_currentToken = _lexicalAnalyzer.GetToken();
expression = Factor();
expression=new UnaryExpression(expression,old==Token.Add?Operator.Plus:Operator.Minus);
}
else
{
throw new Exception("error");
}
return expression;
}
最后生成的树结构如下所示:
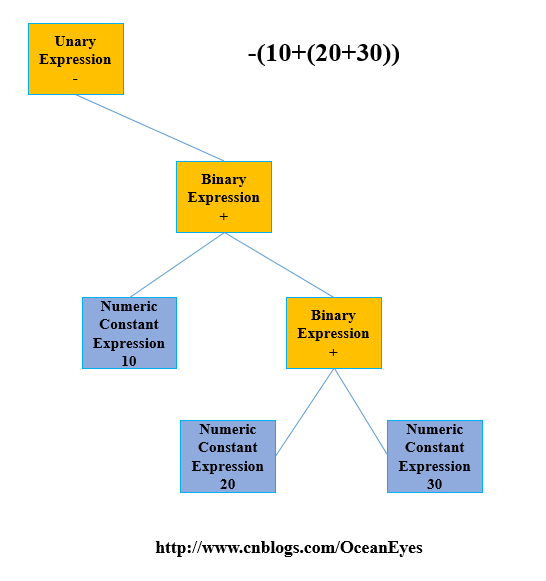
小结###
本文为大家介绍了怎样从编译原理的角度来实现一个解释器。在游戏领域,需要解释器来解释自定义的『公式』。这个『公式』的语法往往是和上下文无关的,又被称为BNF范式。解释器的核心就是怎样构建一棵抽象的表达式树,这需要词法分析和语法分析的相关知识。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号