bzoj3283: 运算器

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <cmath> 5 #include <algorithm> 6 using namespace std; 7 typedef long long int64; 8 int Case; 9 #define maxn 200005 10 #define maxm 600005 11 int now[maxn],prep[maxm]; 12 int64 val[maxm],pi,pk,t; 13 int64 ksm(int64 x,int64 y,int64 p){ 14 if (y==0) return 1%p; 15 if (y==1) return x%p; 16 int64 d=ksm(x,y/2,p); 17 if (y%2==1) return d*d%p*x%p; 18 else return d*d%p; 19 } 20 int64 exgcd(int64 a,int64 b,int64 &x,int64 &y){ 21 if (b==0){ 22 x=1,y=0; 23 return a; 24 } 25 int64 GCD=exgcd(b,a%b,x,y),temp; 26 temp=x,x=y,y=temp-a/b*y; 27 return GCD; 28 } 29 void insert(int x,int64 y){ 30 int pos=y%maxn; 31 prep[x]=now[pos],now[pos]=x,val[x]=y; 32 } 33 int search(int64 x){ 34 int pos=x%maxn,ans=maxm*4; 35 for (int i=now[pos];i!=-1;i=prep[i]){ 36 if (val[i]==x) ans=min(ans,i); 37 } 38 if (ans<maxm*4) return ans; 39 else return -1; 40 } 41 int64 extanded_baby_step_gaint_step(int64 A,int64 B,int64 C){ 42 int64 tmp,temp=1,x,y,D,R,cnt=0; int pos; 43 for (int i=0;i<32;i++){ 44 if (temp==B) return i; 45 temp=temp*A%C; 46 } 47 D=1; 48 for (temp=exgcd(A,C,x,y);temp!=1;cnt++,temp=exgcd(A,C,x,y)){ 49 if (B%temp) return -1; 50 C/=temp,B/=temp; 51 D=D*(A/temp)%C; 52 } 53 memset(now,-1,sizeof(now)); 54 R=1; tmp=ceil(sqrt(C*1.0)); 55 for (int i=0;i<tmp;i++){ 56 insert(i,R); 57 R=R*A%C; 58 } 59 for (int i=0;i<tmp;i++){ 60 temp=exgcd(D,C,x,y); 61 x=(x%C*(B/temp)%C+C)%C; 62 pos=search(x); 63 if (pos!=-1) return i*tmp+pos+cnt; 64 D=D*R%C; 65 } 66 return -1; 67 } 68 int64 inv(int64 X){ 69 int64 x,y; 70 int64 temp=exgcd(X,pk,x,y); 71 return (x%pk+pk)%pk; 72 } 73 int64 work(int64 n){ 74 if (n==0) return 1LL%pk; 75 int64 ans=1; 76 for (int i=1;i<=pk;i++) if (i%pi) ans=ans*i%pk; 77 ans=ksm(ans,n/pk,pk); 78 int64 k=n%pk; 79 for (int i=1;i<=k;i++) if (i%pi) ans=ans*i%pk; 80 return ans*work(n/pi)%pk; 81 } 82 int64 calc(int64 n,int64 m){ 83 int64 a,b,c; int64 k=0; 84 a=work(n),b=work(n-m),c=work(m); 85 for (int i=n;i;i/=pi) k+=(i/pi); 86 for (int i=n-m;i;i/=pi) k-=(i/pi); 87 for (int i=m;i;i/=pi) k-=(i/pi); 88 return 1LL*ksm(pi,k,pk)%pk*a%pk*inv(b)%pk*inv(c)%pk; 89 } 90 void work1(){ 91 int64 n,m,p; 92 scanf("%lld%lld%lld",&n,&m,&p); 93 printf("%lld\n",ksm(n,m,p)%p); 94 } 95 void work2(){ 96 int64 A,B,C,ans; 97 scanf("%lld%lld%lld",&A,&B,&C); 98 B%=C; 99 ans=extanded_baby_step_gaint_step(A,B,C); 100 if (ans==-1) printf("Math Error\n"); 101 else printf("%lld\n",ans); 102 } 103 void work3(){ 104 int64 n,m,p,temp,x,y,tmp,ans=0; 105 scanf("%lld%lld%lld",&m,&n,&p); 106 t=p; 107 for (int i=2;i<=sqrt(p);i++){ 108 if (t%i==0){ 109 pi=i,pk=1; 110 while (t%i==0){ 111 pk=pk*i; 112 t/=i; 113 } 114 temp=exgcd(p/pk,pk,x,y); 115 tmp=calc(n,m)/temp; 116 x=x*tmp%p*(p/pk)%p; 117 ans=(ans+x)%p; 118 } 119 } 120 if (t>1){ 121 pi=t,pk=t; 122 temp=exgcd(p/pk,pk,x,y); 123 tmp=calc(n,m)/temp; 124 x=x*tmp%p*(p/pk)%p; 125 ans=(ans+x)%p; 126 } 127 printf("%lld\n",(ans%p+p)%p); 128 } 129 int main(){ 130 scanf("%d",&Case); 131 for (int type;Case;Case--){ 132 scanf("%d",&type); 133 if (type==1) work1(); 134 else if (type==2) work2(); 135 else work3(); 136 } 137 return 0; 138 }
题目链接:http://www.lydsy.com/JudgeOnline/problem.php?id=3283
题目大意:
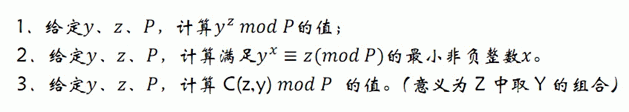
吐槽:HN2016省队集训原题,辣鸡出题人......
做法:对于操作1,没什么好说的,直接上快速幂即可。
对于操作2,如果p是质数,就是BSGS算法,否则,就用扩展BSGS算法;而实际上扩展BSGS可以解决p是质数,所以就不用分类讨论了。
对于(extended)baby_step_gaint_step算法,未完待续......
对于操作3,组合数取模,扩展lucas定理。
对于组合数取模,未完待续......



 浙公网安备 33010602011771号
浙公网安备 33010602011771号