BZOJ3091 城市旅行
把这题放在模拟赛里也真是没谁了
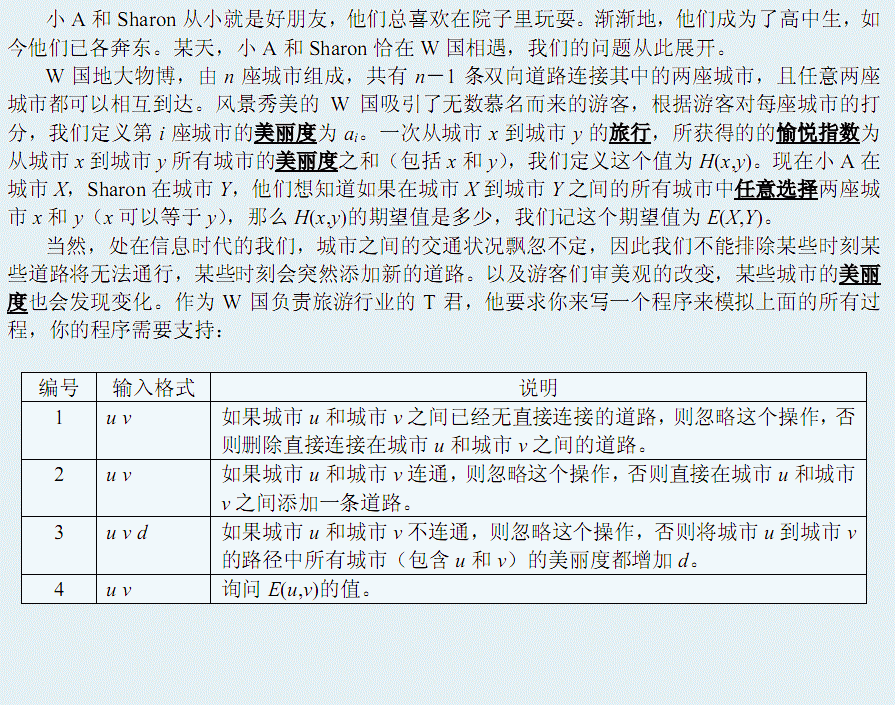
弱智都能看出来这题是$LCT$
然而这题也能把你写成一个弱智
嘿嘿嘿
好了说正经的
维护的答案显然是一条链中每一条子链的点权和之和,最后再与其子链个数作比即可。
其实,不同的$LCT$的题目主要的不同在于$pushup(update)$和$pushdown$,就像线段树一样。仅从我的视角来看,数据结构,一般是使用独特的“结构”来储存数据,在修改与查询之间找到一个的相对平衡的复杂度加速整体的效率。
也就是说,维护结构的部分大体相同,难点只是维护数据的部分(即$pushup、pushdown$等操作)。
那么,类似线段树一样考虑,在把一条链接过来,再接上另一条链(带方向),形成一个新的长链,设这条长链为 链$A \cdot$点$x\cdot $链$B$ 那么这条新的长链的答案(即每一条子链的点权和之和)就是:
$$ANS(A\cdot x \cdot B)=$$
$$ANS(A)+ANS(B)$$
$$+$$
$$Suf(A)\times (Size(B)+1)$$
$$+$$
$$Pre(B)\times (Size(A)+1)$$
$$+$$
$$Val_x\times (Size(A)+1)\times (Size(B)+1)$$
$Pre$表示该链所有包含上端点的子链之和。
$Suf$表示该链所有包含下端点的子链之和。
$Size$表示该链包含的点的数量,$Val$表示点权。
上文的式子的几个部分差不多是分开计算了一条链几部分对答案的贡献,大概思路就是,链左侧的答案加右侧的答案加跨越$x$的答案
介于在$LCT$中,$Splay$以原树中的$Dfs$序为中序遍历维护一条自上而下的链,所以节点$x$左右儿子及其子树代表的恰好分别就是接在$x$上端和下端的链,因此维护$Pre$与$Suf$方便我们更新答案。
$LCT$我并不是太熟练,所以好多操作都打畸形了,模拟赛这道题也爆零了。
不多说了,放代码...
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define M 100010
#define ls c[x][0]
#define rs c[x][1]
using namespace std;
LL read(){
LL nm=0,fh=1;char cw=getchar();
for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
return nm*fh;
}
void write(LL x){if(x>=10) write(x/10);putchar(x%10+'0');}
LL n,m,T,fa[M],c[M][2],val[M],tg[M],sum[M],sz[M],rev[M],ans[M],tpe;
LL S[M],top,pre[M],suf[M],tot[M],dt,u,v,t1,t2;
LL gcd(LL x,LL y){return x%y==0?y:gcd(y,x%y);}
inline void pushdown(LL x){
if(rev[x]) swap(c[ls][0],c[ls][1]),rev[ls]^=1,swap(suf[ls],pre[ls]);
tg[ls]+=tg[x],val[ls]+=tg[x],ans[ls]+=tot[sz[ls]]*tg[x];
dt=tg[x]*(sz[ls]*sz[ls]+sz[ls])/2,pre[ls]+=dt,suf[ls]+=dt,sum[ls]+=sz[ls]*tg[x];
if(rev[x]) swap(c[rs][0],c[rs][1]),rev[rs]^=1,swap(suf[rs],pre[rs]);
tg[rs]+=tg[x],val[rs]+=tg[x],ans[rs]+=tot[sz[rs]]*tg[x];
dt=tg[x]*(sz[rs]*sz[rs]+sz[rs])/2,pre[rs]+=dt,suf[rs]+=dt,sum[rs]+=sz[rs]*tg[x];
tg[x]=rev[x]=val[0]=sum[0]=ans[0]=sz[0]=pre[0]=suf[0]=tg[0]=rev[0]=0;
}
inline void pushup(LL x){
sz[x]=sz[ls]+sz[rs]+1,sum[x]=sum[ls]+sum[rs]+val[x];
pre[x]=pre[ls]+sum[ls]+val[x]+pre[rs]+sz[rs]*(sum[ls]+val[x]);
suf[x]=suf[rs]+sum[rs]+val[x]+suf[ls]+sz[ls]*(sum[rs]+val[x]);
ans[x]=ans[ls]+ans[rs]+(sz[ls]+1)*(sz[rs]+1)*val[x];
ans[x]+=(sz[ls]+1)*pre[rs]+(sz[rs]+1)*suf[ls];
}
bool isroot(LL x){return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;}
void rotate(LL x){
LL tp=fa[x],dtp=fa[fa[x]],ms,ds;
if(!isroot(tp)){
if(c[dtp][0]==tp) c[dtp][0]=x;
else c[dtp][1]=x;
}
if(c[tp][0]==x) ms=0,ds=1;
else ms=1,ds=0;
fa[x]=dtp,fa[tp]=x,fa[c[x][ds]]=tp;
c[tp][ms]=c[x][ds],c[x][ds]=tp;
pushup(tp),pushup(x);
}
void splay(LL x){
top=1,S[top]=x;
for(LL y=x;!isroot(y);y=fa[y]) S[++top]=fa[y];
while(top) pushdown(S[top]),top--;
while(!isroot(x)){
LL tp=fa[x];
if(isroot(tp)) return rotate(x);
if(c[c[fa[tp]][0]][0]==x) rotate(tp);
else if(c[c[fa[tp]][1]][1]==x) rotate(tp);
else rotate(x);
}
}
void access(LL x){for(LL last=0;x;last=x,x=fa[x]) splay(x),rs=last,pushup(x);}
void chroot(LL x){access(x),splay(x),rev[x]^=1,swap(ls,rs),swap(suf[x],pre[x]);}
LL fdroot(LL x){splay(x);while(ls)x=ls;return x;}
LL getfa(LL x){while(fa[x]) x=fa[x];return x;}
void cut(LL x,LL y){chroot(x),access(y),splay(y);if(fa[x]==y) c[y][0]=fa[x]=0;}
void link(LL x,LL y){if(getfa(x)!=getfa(y)) chroot(x),access(y),splay(y),fa[x]=y;}
void add(LL x,LL y){
if(getfa(x)!=getfa(y)) return;
chroot(y),access(x),splay(x),tg[x]+=m;
sum[x]+=sz[x]*m,val[x]+=m,ans[x]+=tot[sz[x]]*m;
pre[x]+=m*((sz[x]*sz[x]+sz[x])/2),suf[x]+=m*((sz[x]*sz[x]+sz[x])/2);
}
void query(LL x,LL y){
if(getfa(x)!=getfa(y)){puts("-1");return;}
chroot(y),access(x),splay(x);t1=ans[x],t2=(sz[x]*sz[x]+sz[x])/2;
dt=gcd(t1,t2),write(t1/dt),putchar('/'),write(t2/dt),putchar('\n');
}
int main(){
n=read(),T=read(),tot[1]=1;
for(LL i=2;i<=n;i++) tot[i]=tot[i-1]+(i*i+i)/2;
for(LL i=1;i<=n;i++) val[i]=read(),sum[i]=ans[i]=pre[i]=suf[i]=val[i];
for(LL i=1;i<n;i++) u=read(),v=read(),link(u,v);
while(T--){
tpe=read(),u=read(),v=read();
if(tpe==1) cut(u,v);
else if(tpe==2) link(u,v);
else if(tpe==3) m=read(),add(u,v);
else query(u,v);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号