BZOJ4817 [SDOI2017]树点涂色
4817: [SDOI2017]树点涂色
Description
Bob有一棵n个点的有根树,其中1号点是根节点。Bob在每个点上涂了颜色,并且每个点上的颜色不同。定义一条路
径的权值是:这条路径上的点(包括起点和终点)共有多少种不同的颜色。Bob可能会进行这几种操作:
1 x:
把点x到根节点的路径上所有的点染上一种没有用过的新颜色。
2 x y:
求x到y的路径的权值。
3 x
在以x为根的子树中选择一个点,使得这个点到根节点的路径权值最大,求最大权值。
Bob一共会进行m次操作
Input
第一行两个数n,m。
接下来n-1行,每行两个数a,b,表示a与b之间有一条边。
接下来m行,表示操作,格式见题目描述
1<=n,m<=100000
Output
每当出现2,3操作,输出一行。
如果是2操作,输出一个数表示路径的权值
如果是3操作,输出一个数表示权值的最大值
题目简述
定义树根为1
定义路径权值:连续颜色段的数量
维护一棵树,支持如下三种操作:
1、将x点到根路径上每一个点都修改成新的颜色
2、查询某条路径权值
3、查询某颗子树内点到1路径最大权值。
题解
一道非常典型的数据结构之间的相互应用的题,利用$LCT$维护路径,利用线段树维护点权最值。
我们还是先从树剖想起,于是就发现树剖套线段树能完美的解决前两种操作,但对第三种操作却束手无策。树链剖分的限制是,在任何时刻求单个点到跟的路径权值都需要$O(log(n))$的复杂度,并且无法区间求最值,所以树剖这条路看起来并不是这么可行(但据我们机房某julao说可以直接用树剖套两个线段树搞定)。
为了方便,我们设一个点的点权为其到根节点的路径权值。
我们换个思路,不难发现,对于第二种操作,假设给定了路径两个端点为$(u,v)$,设$lca(u,v)=k$,设$D(x)$为$x$的点权,则$(u,v)$路径权值为和$D(u)+D(y)-2D(k)+1$,就把我第二种操作转化为求某个点的点权了。所欲对于后两个操作,我们现在只需要维护区间点权最值即可。
再来关注修改,我们发现,修改与$LCT$中的$access$操作十分相似,我们考虑修改对每个点的答案的影响,如下图:
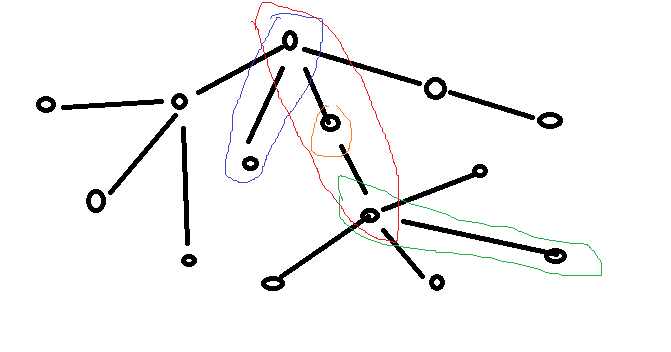
红色部分是我们要修改的,对于每一个和红色有重叠的颜色段(即$access$操作中每一条原来的重链),重叠部分的染色对于原颜色段的除去与要修改的重叠以外部分(若不存在则不考虑)所在的整颗的子树的答案有+1的贡献(即图中各个颜色段与红色不重叠的部分);对于除去顶部的颜色段以外的所有颜色段的顶端的子树有-1的贡献。
对应的$LCT$中就恰好是,$access$时:
对于断开某条重链,就把下方的断点所在子树答案+1;
对于连接一条链,就把下方连接点所在子树答案-1;
用线段树维护即可,复杂度约为$O(n\cdot log^2(n))$。
注意初始时每个点颜色不同,点权为其深度。
AC代码如下:
#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define mid (l+r>>1)
#define M 100010
#define ls c[x][0]
#define rs c[x][1]
using namespace std;
int read(){
int nm=0,fh=1;char cw=getchar();
for(;!isdigit(cw);cw=getchar()) if(cw=='-') fh=-fh;
for(;isdigit(cw);cw=getchar()) nm=nm*10+(cw-'0');
return nm*fh;
}
void write(int x){
if(x>=10) write(x/10);
putchar(x%10+'0');
}
int n,m,fs[M],tmp,to[M<<1],nt[M<<1],st[M<<2][20];
int dfn[M],tk[M],cnt,dep[M],sz[M],fst[M],tot,fa[M];
int p[M<<2],tg[M<<2],lg[M<<2],sq[30];
int u,v,T,c[M][2],tpe;
void link(int x,int y){nt[tmp]=fs[x],fs[x]=tmp,to[tmp++]=y;}
void dfs(int x){
dfn[x]=++cnt,st[++tot][0]=dfn[x];
sz[x]=1,fst[x]=tot,tk[cnt]=x;
for(int i=fs[x];i!=-1;i=nt[i]){
if(dep[to[i]]>0) continue;
dep[to[i]]=dep[x]+1,dfs(to[i]),fa[to[i]]=x;
st[++tot][0]=dfn[x],sz[x]+=sz[to[i]];
}
}
void init(){
lg[0]=-1,sq[0]=1;
for(int i=1;i<=tot;i++) lg[i]=lg[i>>1]+1;
for(int i=1;i<=20;i++) sq[i]=(sq[i-1]<<1);
for(int j=1;j<19;j++){
for(int i=1;i+sq[j]-1<=tot;i++){
st[i][j]=min(st[i][j-1],st[i+sq[j-1]][j-1]);
}
}
}
int lca(int x,int y){
int t1=fst[x],t2=fst[y],len;
if(t1>t2) swap(t1,t2);
len=t2-t1+1;
return tk[min(st[t1][lg[len]],st[t2-sq[lg[len]]+1][lg[len]])];
}
void pushdown(int x){
tg[x<<1]+=tg[x],p[x<<1]+=tg[x];
tg[x<<1|1]+=tg[x],p[x<<1|1]+=tg[x];
tg[x]=0; return;
}
void pushup(int x){p[x]=max(p[x<<1],p[x<<1|1]);}
void build(int x,int l,int r){
if(l==r){p[x]=dep[tk[l]];return;}
build(x<<1,l,mid),build(x<<1|1,mid+1,r),pushup(x);
}
void add(int x,int l,int r,int L,int R,int dt){
if(r<L||R<l) return;
if(L<=l&&r<=R){tg[x]+=dt,p[x]+=dt;return;}
pushdown(x),add(x<<1,l,mid,L,R,dt);
add(x<<1|1,mid+1,r,L,R,dt),pushup(x);
}
int query(int x,int l,int r,int L,int R){
if(r<L||R<l) return 0;
if(L<=l&&r<=R) return p[x];
pushdown(x); int now=query(x<<1,l,mid,L,R);
now=max(query(x<<1|1,mid+1,r,L,R),now);
pushup(x); return now;
}
bool isroot(int x){return c[fa[x]][0]!=x&&c[fa[x]][1]!=x;}
void rotate(int x){
int tp=fa[x],dtp=fa[fa[x]],ds,ms;
if(!isroot(tp)){
if(c[dtp][0]==tp) c[dtp][0]=x;
else c[dtp][1]=x;
}
if(c[tp][0]==x) ms=0,ds=1;
else ms=1,ds=0;
fa[x]=dtp,fa[tp]=x,fa[c[x][ds]]=tp;
c[tp][ms]=c[x][ds],c[x][ds]=tp;
}
void splay(int x){
while(!isroot(x)){
int tp=fa[x];
if(isroot(tp)) return rotate(x);
if(c[c[fa[tp]][0]][0]==x) rotate(tp);
else if(c[c[fa[tp]][1]][1]==x) rotate(tp);
else rotate(x);
}
}
void access(int x){
int now;
for(int last=0;x>0;rs=last,last=x,x=fa[x]){
splay(x);
if(rs>0){
for(now=rs;c[now][0]>0;now=c[now][0]);
add(1,1,n,dfn[now],dfn[now]+sz[now]-1,1);
}
if(last>0){
for(now=last;c[now][0]>0;now=c[now][0]);
add(1,1,n,dfn[now],dfn[now]+sz[now]-1,-1);
}
}
}
int main(){
n=read(),T=read(),memset(fs,-1,sizeof(fs));
for(int i=1;i<n;i++) u=read(),v=read(),link(u,v),link(v,u);
dep[1]=1,dfs(1),init(),build(1,1,n);
while(T--){
tpe=read(),u=read();
if(tpe==3) write(query(1,1,n,dfn[u],dfn[u]+sz[u]-1)),putchar('\n');
else if(tpe==1) access(u);
else{
v=read(),m=lca(u,v);
u=query(1,1,n,dfn[u],dfn[u]);
v=query(1,1,n,dfn[v],dfn[v]);
m=query(1,1,n,dfn[m],dfn[m]);
write(u+v-m-m+1),putchar('\n');
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号