平衡树 学习笔记
平衡树大名早有耳闻,而且据说会成为新考点。
今晚zhx大佬讲了一下基本概念和代码实现,我就把当时手写的笔记搬上来吧。
(中间被一找我debug代码的人卡了一个小时,我tm早知道不该帮他。。。就是道大爆搜自己看题解不行吗。。。。只能过样例但是爆0我怎么知道你错哪了。。。有毒吧卧槽。。)
(其实有很多不和谐的话,我自动屏蔽吧)
特别长的笔记,看看今晚能不能写完吧。。
由于时间仓促,再加算法略加高级,所以我的措辞应该会有严重不规范甚至完全错误的地方,还请大佬看到后指正,欢迎私信炮轰。
只能作为参考,在定型之前不具备客观上的学习意义,各位看时请带着debug的眼神来看。
- 平衡树的概念
我们假设您知道线段树是怎么回事。我们知道,线段树可以进行区间操作,比如区间修改和区间查询,但是没有办法去执行一个增加和删除的操作。
平衡树在功能上解决了线段树无法进行增删的缺陷。
这次主要写两个操作,一个插入,一个删除。
- 平衡树常见的类型
当然有什么替罪羊树,朝鲜树之类的奇怪的平衡树就不说了。。
SBT:Size Balanced Tree,节点大小平衡树。优点是快而且相对好写,缺点是相比于其他的平衡树功能不太全。
treap:这也是今天课上讲的平衡树,其单词由tree和heap融合而成,也叫树堆。优点是比SBT更好写,但是速度比SBT慢。
(我记得rqy大佬在Day0的时候给我说过一个叫二叉搜索树的东西,好像就是它了)
RBT:Red Black Tree,红黑树,它比SBT还快,但是初学者的话。。。。大概3.5h左右能写出来。。。。
splay:这个数据结构据说之前一段时间挺火,学平衡树的各位都要学这个算法。。。但是它。。。。。
特 别 慢 , 常 数 巨 大 无 比。
怎么个慢法?前三个平衡树单次操作都是基本上O(logn)的,splay的单次操作虽然也写作O(logn),但是由于其巨大的常数,实际跑起来和O(sqrt(n))差不多,并且不太好写。
但是功能极强。
平衡树常见的一个操作叫旋转,今天讲的这个是没有旋转操作的可持久化treap,(虽然可持久化没讲完)
- 一个普通的treap(二叉搜索树)是什么样的,有什么基本性质?
先放结论。
对于一个点,其左儿子永远比它小, 右儿子永远比它大。推论:对一个这样的treap,其中序遍历是有序的。
对于一个T = {1,2,3,4,5},treap长的是这样的:
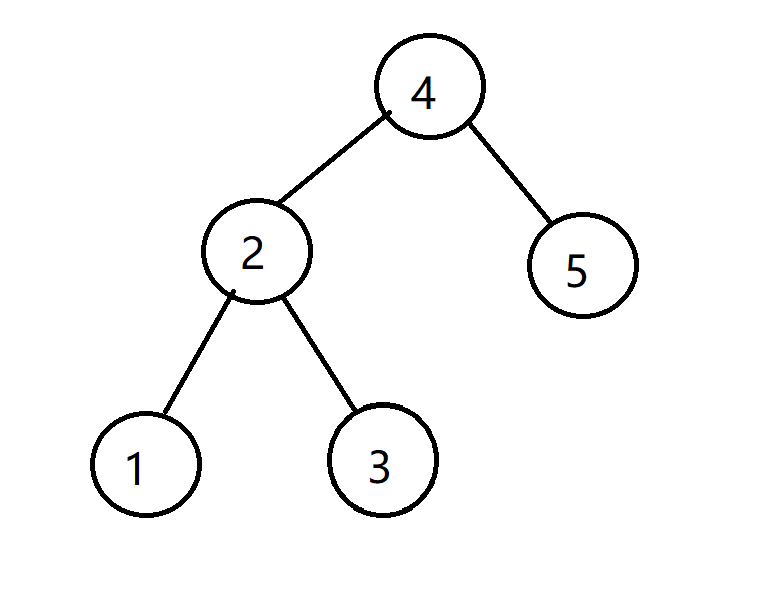
看一下,是不是满足上面那个性质啊。
上面我们说到插入操作。那么如果我要插入一个2.33,这个点应该在哪呢?
既然插入,那么这个插入的位置一定要合法,也就是说,插入之后,也一定要满足这个性质。
正常向的做法:我们从根节点开始比对,发现根节点是4,比2.33大,那么我们就去它的左儿子找位置,因为左儿子永远比根节点小。然后找到2,发现2比2.33大,那么我们就去2的右儿子找位置。然后找到3,发现3比2.33大,按照规律应该是找左儿子,但是3号点已经是最底端没有儿子了,怎么办?其实已经找到了,就在3的左儿子那里新开一个点,把2.33放进去即可。
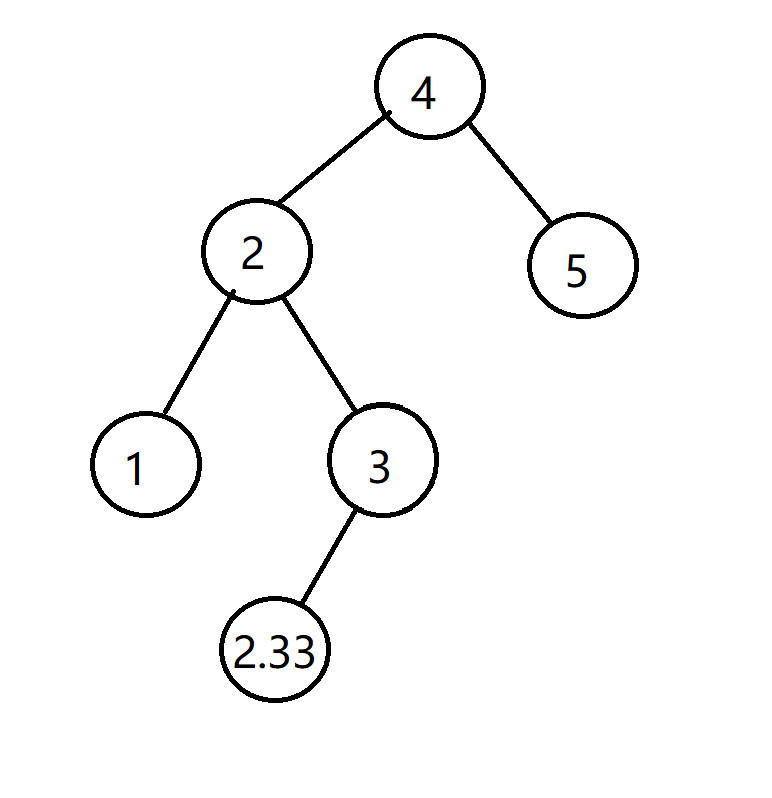
但我们发现,这样的操作如果变多了,树的某个链就有可能会变得很长很长,所以这样的插入方法插入的深度不会很深,这可以叫不平衡。但我们是平衡树啊,一定得想办法让它平衡才行。
其实不同的平衡树那些不同的叫法,实质上都是平衡手段不同。
这里补充一个操作,询问区间和。
请看上面第一个图,如果我要询问区间[1,4]之和,线段树的做法肯定是分成左半段+右半段,然后把两个子节点的权值加起来。而平衡树不是,平衡树会把整个区间拆成诸如[1,3],[4,4],[5,5]这样的三段(也就是会单独把根节点拆开),然后再去求解区间和。
回归正题,插入操作。
我们之前说treap叫树堆,这里拆分成的tree代表一般平衡树,而heap代表一个堆(理论上大根小根都行,这里默认大根,下文讨论全部基于大根堆),其实堆不也是一种二叉树的形式吗。。它要求每个点的值都要比任何一个子节点都大,也就是从叶到根这个值是单调递增的。
但是,细心的读者会发现,堆和平衡树的性质其实是矛盾的。那么我们应该怎么去解决这个矛盾呢?其实这里有一个合并思想,那就是在treap里面每个点都存储两个值,即key和value。
这里的key满足堆的性质,而value就是treap里原来存的那个值,就是中序遍历满足平衡树性质那个。
key的值在实际应用中一般都采用随机化。(rqy:为了防止出题人卡你)
其实使用随机化可以保证树的深度会在logn级别。
这样我们就得到了一个比较正经的treap。
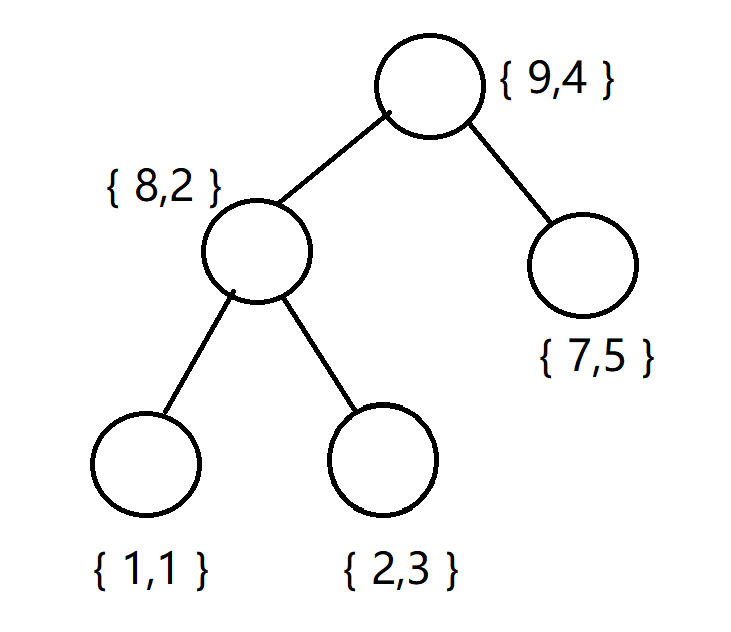
(大括号内第一个值是key,第二个值是value,key已经随机化)
回到我们最初的问题。如果要插入一个2.33,插哪里?
我们假设与2.33相对应的key值是6,其他数不变。
如果再用之前那个查询的方法显然是不可以的。我们需要新方法。
首先我们列表:
| key | 1 | 8 | 2 | 9 | 7 | 6 |
| value | 1 | 2 | 3 | 4 | 5 | 2.33 |
首先很显然呢根节点应该是{9,4},然后左儿子是{8,2},右儿子是{7,5}。对于{8,2}这个点,其左儿子是{1,1},右儿子是{6,2.33},{6,2.33}没有左儿子,只有右儿子{2,3}
各位看一下, 是不是两个性质都满足了?
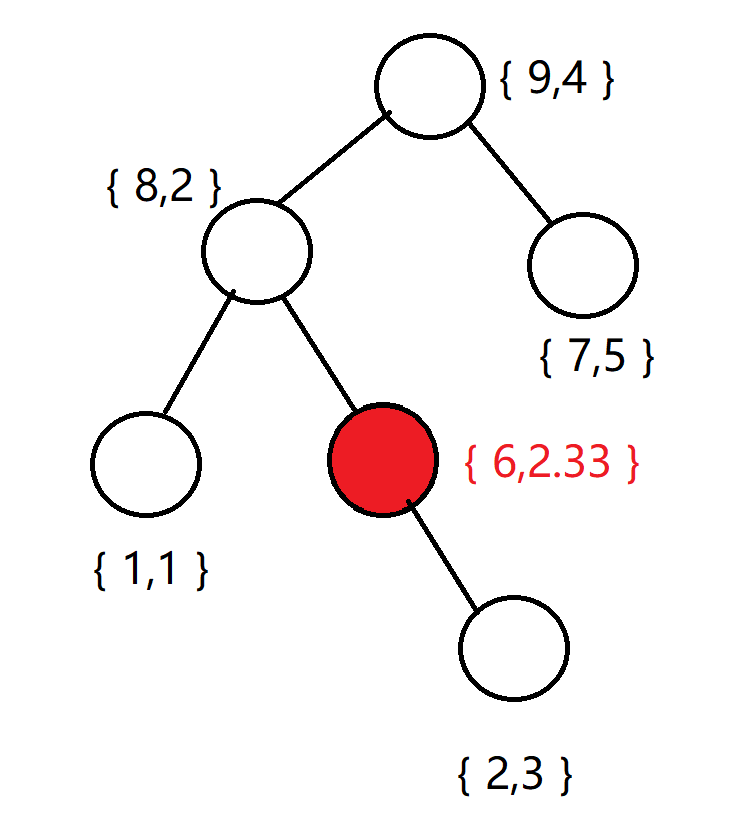
接下来便是重头戏,merge操作和split操作。
对于一个merge操作,有两个参数p1和p2,这个操作可以将以p1为根节点的treap与以p2为根节点的treap合并成一个新的treap,并返回这个treap。
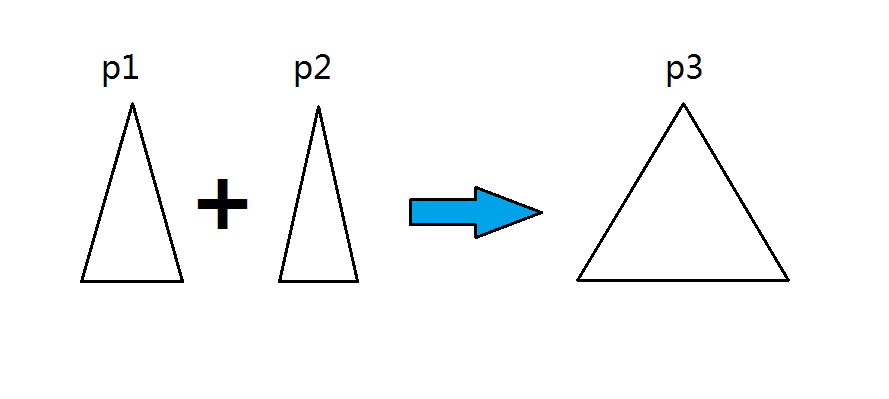
但这个操作是有一个前提的,那就是p1要小于等于p2。换句话说,是要让p1最大的节点的value值小于等于p2的最小的节点的value值。
下一个操作叫split,它也是接受两个参数,一个是p一个是k。这个操作的意思是在以p为根的treap中把前k小的数拿出来,组成一个新treap。相当于一个拆分操作,把这个有n个节点的treap p拆成一个有k个节点的p1,一个有n-k个节点的p2。
不难看出,split与merge操作互逆。
这个拆分也是有特性的。它要求拆分出的p1小于等于p2。意思和上面merge是一样的。

我们来演示一下这个插入和删除的过程。
比如有一棵树P={1,2,3,4,5},我们要插一个2.33进去,在查找过程中发现了2.33<3,在3前面有两个元素,所以我们的操作是:首先执行split(p,2),把这棵树分成两棵比较小的树,这样分完应该是有p1{1,2}和p2{3,4,5}。下一步要怎么做?我们建立一个新treap,这个新treap只有2.33这个值,我们假设这个新treap为newp,然后去执行merge(merge(p1,newp),p2)就可以得到一个插入这个点的新的treap。
我把它叫作:“三树并一插新点”。
删除过程。我们假设有P={1,2,3,4,5},然后我们要把里面的{2}拿出来,这个要怎么做?做法是split两次,在{2}的左边和右边各一次,也就是要把树拆成这样的样子:{1}{2}{3,4,5},然后把{1}和{3,4,5}合并一下,就完成了删除操作。这一步操作其实是把{2}孤立了出来,使之不再属于原来的treap。
我把它叫作:“二(子)树合并孤立点”。
在实际操作上,假设我们要执行merge(p1,p2),我们知道对于treap的一个节点是有key和value两个值的,在实际操作的时候,还要记录某个点的的左儿子l和右儿子r。
合并的话你肯定是要先决定根是哪个的。根据treap的堆性质,其最上面的点key值应该最大,而在原来的p1和p2里面也只可能会是两个根节点p1和p2最大,所以只可能会有这两个点中的其中一个当根。我们分两种情况,第一种是p1.key > p2.key,那么显然是以p1为根的吧。根据之前讨论的性质,插入要保证p1是小于等于p2的,所以p2要放在哪?是p1的右儿子。而p1的左儿子不是p2,所以左儿子维持不变,仍然是p1.l,而右儿子就会变成merge(p1.r,p2)。
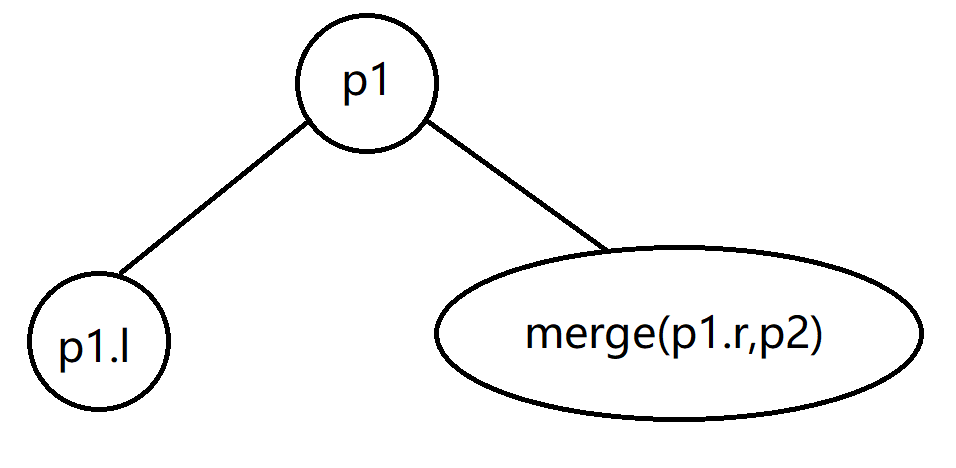
这个操作的优先级用堆的key值可以保证。可以看出这个操作是递归的。merge函数的返回值就是merge出的树的根节点。
我们考虑第二种情况,p1.key < p2.key,同理,可以得到
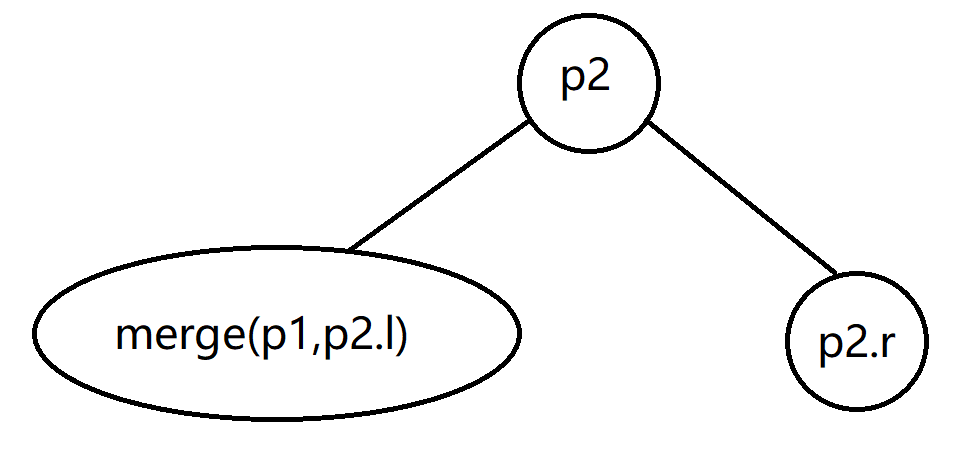
这个操作也是递归的。
实际操作的split是如何呢?
我们再来回顾一下split的定义:一个操作split(p,k),它会把以p为根节点的treap的前k小节点拆出来,我们依然是需要记录p的key,value,l和r。同时还要多记录一个p.size,它代表树中有多少节点。我们知道这个split是会把一个p拆成p1和p2的,这个p1便是理想状态下前k小的左子树,p2则包含p和p.r。
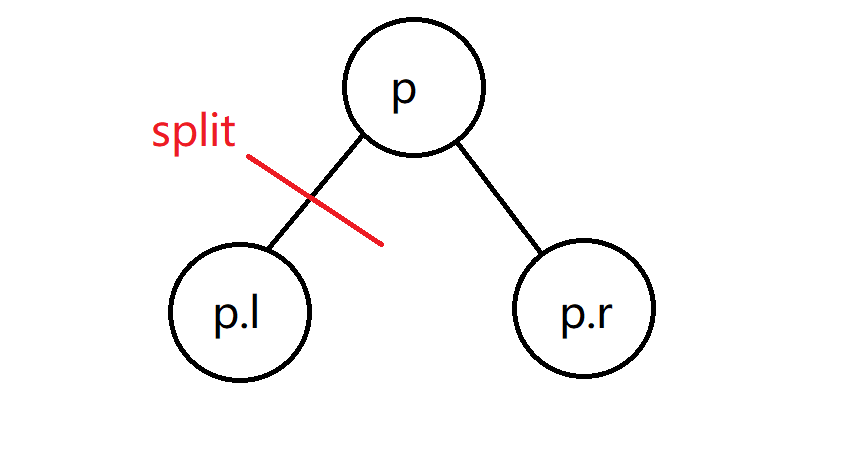
这里分三种情况。第一种是k小于等于p.l.size,那么我们split(p.l,k),它返回两棵树{p1,p2},我们选其中的p1,不选p2的原因是p2并不包含{p,p.r},那么怎么办?只需要再构造一个{p,p.l,p.r}的treap返回就好。
看到这里您也许就明白了,split返回两棵树,返回值有两个,实际写法上一般返回一个对组pair。
第二种情况,k等于p.l.size+1,这里返回{p,p.l}与{p.r}两棵树。
第三种情况,k大于p.l.size+1,返回{p,p.l,p.r}与{p2}。
我当时记的差不多就这些。。。。。找个时间就发下代码吧。。。
接下来是二分图匹配和网络流(dinic)的算法整理。

