NOIP 2011 普及组 T4 表达式的值 栈

题目

题目描述

对于1 位二进制变量定义两种运算：

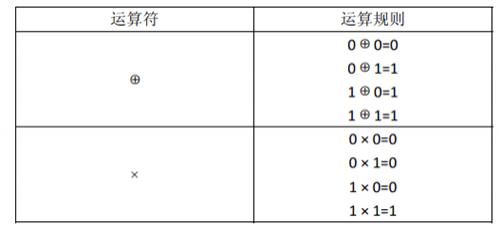
运算的优先级是：

  1. 先计算括号内的，再计算括号外的。

  2. “× ”运算优先于“⊕”运算，即计算表达式时，先计算× 运算，再计算⊕运算。例如：计算表达式A⊕B × C时，先计算 B × C，其结果再与 A 做⊕运算。

现给定一个未完成的表达式，例如_+(_*_)，请你在横线处填入数字 00 0 或者 111 ，请问有多少种填法可以使得表达式的值为 00 0 。

输入输出格式

输入格式：

共 2 行。

第1 行为一个整数 LLL ，表示给定的表达式中除去横线外的运算符和括号的个数。

第2 行为一个字符串包含 LLL 个字符，其中只包含’（’、’）’、’+’、’*’这 444 种字符，其中’（’、’）’是左右括号，’+’、’*’分别表示前面定义的运算符“⊕”和“×”。这行字符按顺序给出了给定表达式中除去变量外的运算符和括号。

输出格式：

共1 行。包含一个整数，即所有的方案数。注意：这个数可能会很大，请输出方案数对 1000710007 10007 取模后的结果。

输入输出样例

输入样例#1： 复制 
4
+(*)
输出样例#1： 复制 
３

说明

【输入输出样例说明】

  给定的表达式包括横线字符之后为：_+(_*_) 

  在横线位置填入(0 、0 、0) 、(0 、1 、0) 、(0 、0 、1) 时，表达式的值均为0 ，所以共有3种填法。 

【数据范围】

对于 20%20\%20% 的数据有 0≤L≤10 0 ≤ L ≤ 100≤L≤10 。

对于 50%50\%50% 的数据有 0≤L≤1,0000 ≤ L ≤ 1,0000≤L≤1,000 。

对于 70%70\%70% 的数据有 0≤L≤10,000 0 ≤ L ≤ 10,0000≤L≤10,000 。

对于 100%100\%100% 的数据有 0≤L≤100,000 0 ≤ L ≤ 100,0000≤L≤100,000 。

对于 50%50\%50% 的数据输入表达式中不含括号。

分析

首先这道题目，我们要先搞清楚我们如何从前往后退出答案。可以肯定的是，在出现某个特定符号的时候，我们要知道如何从已知答案中推出之后的答案。这其实就是一个用公式递推的过程。每一步计算下一步答案为0或1的方法数：设两个步骤的运算结果经过每个符号到一个结果时，第一个运算结果算出0的方案数为t1，1的方案数为t2。第二个算出0的方案数为t3，算出1的方案数为t4，则有： 当符号是“⊕”时，得到0的方案数为t1*t3，1的方案数：t1*t4+t2*t3+t2*t4 当符号是“×”时，得到0的方案数为t1*t3+t1*t4+t2*t3，1的方案数：t2*t4 用一个栈记录下来即可。

然后按以下方法计算：

  1. 如果是左括号，就直接进栈；
  2. 如果是右括号，就一直弹栈并加以计算，直到弹到左括号；
  3. 如果是运算符，则弹栈，直到这个运算符的优先级大于符号栈栈顶的符号的优先级 或是左括号或栈空，然后将运算符进栈； 最后再将栈中残余的符号和结果一直弹到只剩一个结果，这个就是最后的结果。

程序

 1 #include <bits/stdc++.h>
 2 const int M=10007,N=100005;
 3 int n, u[N], v[N], top, k;
 4 char c[N], S[N], ans[2*N];
 5 int main()
 6 {
 7     scanf("%d",&n);
 8     scanf("%s",c);
 9     ans[++k]='.';
10     for(int i = 0; c[i]; i++)
11     {
12         if(c[i] == '(' || c[i] == '*')
13             S[++top] = c[i];
14         if(c[i] == '+')
15         {
16             while(S[top] == '*')
17                 ans[++k] = S[top--];
18             S[++top] = c[i];
19         }
20         if(c[i] == ')')
21         {
22             while(S[top] != '(')
23                 ans[++k] = S[top--];
24             top--;
25         }
26         if(c[i] != '(' && c[i] != ')')
27             ans[++k]='.';
28     }
29     while(top > 0)
30         ans[++k] = S[top--];
31     for(int i = 1; i <= k; i++)
32     {
33         if(ans[i] == '.')
34         {
35             u[++top] = 1;
36             v[top] = 1;
37         }
38         if(ans[i] == '*')
39         {
40             top--;
41             u[top] = (u[top+1]*v[top]+u[top]*v[top+1]+u[top]*u[top+1])%M;
42             v[top] = v[top]*v[top+1]%M;
43         }
44         if(ans[i] == '+')
45         {
46             top--;
47             v[top] = (u[top+1]*v[top]+u[top]*v[top+1]+v[top]*v[top+1])%M;
48             u[top] = u[top]*u[top+1]%M;
49         }
50     }
51     printf("%d",u[1]);
52     return 0;
53 }

 

posted @ 2018-06-25 22:33  OptimusPrime_L  阅读(493)  评论(0)  编辑  收藏  举报