[校内]机器人
2023-10-02
题目
难度&重要性(1~10):9
题目来源
luogu
题目算法
建图,树链剖分,线段树
解题思路
一道很好的模型转换题。
我们看完题目后首先就可以发现其实一步一步的移动是影响我们的,因为如果是存在可行方案时,那么一定有一种方案是每一个囚犯转移时可以直接 \(S_i\to T_i\) 的。
证明也非常简单,如果当前存在一种可行方案需要 \(S_i\to x\) 停顿一下,再 \(x\to T_i\)。则说明在点 \(x\) 存在另一名囚犯,需要等另一名囚犯转移了再进行移动。那么我们就完全可以先让另一名囚犯转移,然后在一步到位 \(S_i\to T_i\)。
那么无可行方案的条件也就很明显了:当存在点 \(x\) 移动前需要点 \(y\) 移动,但是点 \(y\) 需要点 \(x\) 先移动再移动。换句话说就是形成了一个环。
判断一张图上是否存在环非常简单,只需要进行一个拓扑排序就可以了。
那么下一个问题,也是本题的核心:如何去建图呢?
简单的建图方式很明显不行,我们因为就是要判断是否存在环,而我们有需要保证 \(S_i\to T_i\) 有边,而且要对于路径上每一个点都要有边,那么我们就需要建两组一模一样的点:
-
第一组我们将点 \(i\) 连向除 \(T_i\) 外 \(S_i\to T_i\) 上的所有点,\(T_i\) 连向点 \(i\);
-
第二组我们将除 \(S_i\) 外 \(S_i\to T_i\) 上的所有点连向点 \(i\),点\(i\) 连向 \(S_i\)。
例如,对于 \(3\to 4\) 时,建图就长这样:
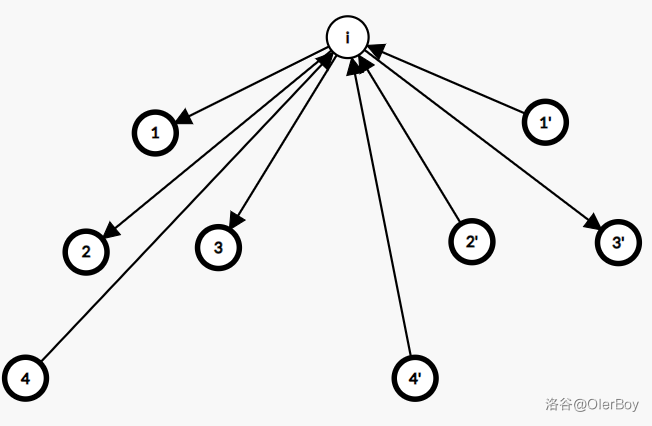
而,如果 \(i\) 与 \(j\) 冲突了,就会出现环:
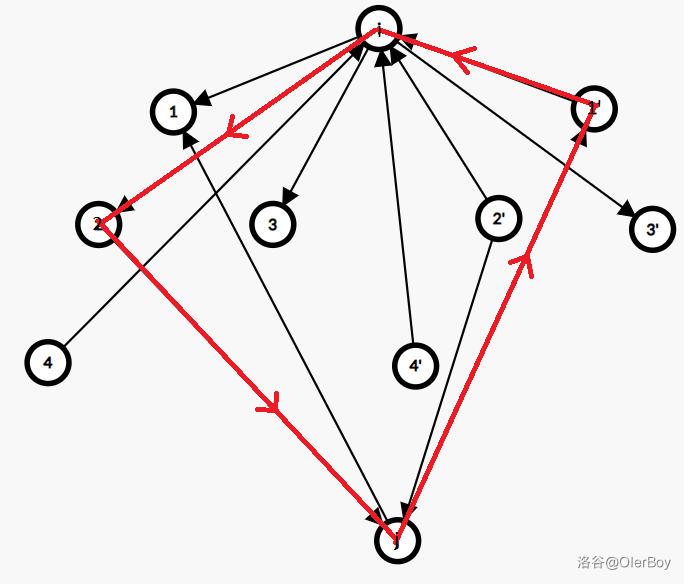
这样我们就可以把图建出来了,拓扑就行了。
但如果这样这道题就做完了它就不是紫题了。因为我们发现暴力建图的时间复杂度是 \(O(n^2)\) 的。仔细分析发现,我们的对于区间连边 \(O(n)\) 的时间复杂度是接受不了的,考虑优化。
由于我们的操作是对于一个树上连续的区间连边,我们就可以树链剖分加线段树来优化。先用树链剖分把树转成区间,再把区间放到线段树上,每次连边就直接连向线段树就好了。
时间复杂度是 \(O(n\log ^2n)\) 的。
完成状态
已完成

