后缀数组学习笔记
后缀数组是什么
后缀数组就是主要处理字符串后缀问题的，它的实现算法主要有两种：倍增法和 DC3，复杂度分别是 \(O(n\log n)\) 和 \(O(n)\)。这里由于 DC3 代码答辩且难以理解，我就只写了倍增法的实现。
例题引入
题目大意
读入一个长度为 \(n\) 的由大小写英文字母或数字组成的字符串，把这个字符串的所有非空后缀按字典序从小到大排序，然后按顺序输出后缀的第一个字符在原串中的位置。位置编号为 \(1\) 到 \(n\)。
前置芝士
算法
后缀数组记录的就是字符串第 \(i\) 个后缀的排名。
比如一个字符串 \(S=abaababa\) 的后缀就是：
如果我们暴力去提取出 \(S\) 的所有后缀在给它排序显然是不行的，因为它的时间复杂度是 \(O(n^2\log n)\) 的。
倍增法
既然单纯的暴力不行，我们就需要考虑用倍增来处理。
倍增法的主要思想是：
每次将所有后缀按照前 \(2^k\) 个字符排序，最后得出所有后缀的排序。
这样问题就转化为了:现在已知所有后缀关于前 \(2^{k−1}\) 个字符的排序，要对所有后缀排序按前 \(2^k\) 个字符排序。
那么我们就可以将前 \(2^k\) 个字符分为两部分，每一部分的长度都是 \(2^{k−1}\)，并且这两部分按照字典序排序后的名次是已知的。
这里我们定义前一部分的排名为第一关键字 \(key1\)，后一部分的排名为第二关键字 \(key2\)。然后每次按照关键字进行排序，更新 \(rank\) 数组，得到新的排名。
这就是倍增法对后缀数组的处理，比如当处理 \(S=aabaaaab\) 时过程如图：
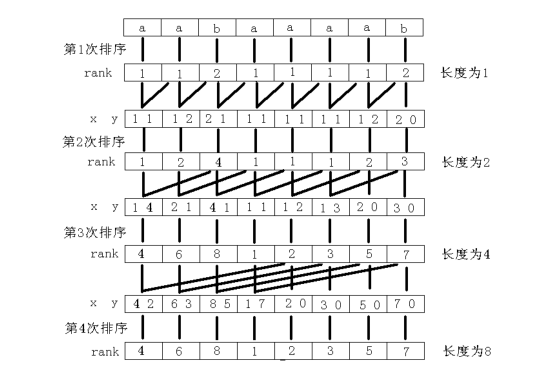
注意，这里处理第一第二关键字排序时，需要先按第一关键字的大小排序，再用第二关键字来排，其思想与基数排序很像。
由于字符串的每个后缀都是不同的(至少长度不同)，所以最后得到的 \(rank\) 数组里的数必定是互不相同的。同样，如果再做第 \(k\) 次倍增时，得到的 \(rank\) 数组如果已经互不相同了，那么就说明已经找到了最终的 \(rank\) 数组，可以直接退出循环了。
实现方法
要想通过倍增法求出后缀数组有两种排序方法。
快速排序 \(O(n\log ^2n)\)
用快速排序来做倍增法是很直观，有助于初学者更好地理解后缀数组-倍增法的思路，代码也很简单。
Code
#include<bits/stdc++.h>
#define int long long
#define N 1000005
#define Mod 1000000007
#define For(i,j,k) for(long long i=j;i<=k;++i)
#define FoR(i,j,k) for(long long i=j;i<k;++i)
#define FOR(i,j,k) for(long long i=j;i>=k;--i)
using namespace std;
struct Node{
int key1,key2,i;
}d[N];
int n,rk[N],sa[N];
string s;
inline bool cmp(Node a,Node b){
if(a.key1<b.key1)return 1;
if(a.key1>b.key1)return 0;
if(a.key2<b.key2)return 1;
if(a.key2>b.key2)return 0;
return a.i<b.i;
}
void SA(){
For(i,1,n)rk[i]=s[i]-'0'+1;//预处理长度为1的子串
for(int l=1;(1<<l)<n;l++){//倍增
int len=1<<(l-1);//已处理的长度
For(i,1,n){//处理第一第二关键字以及它所在的后缀位置
d[i].key1=rk[i];
d[i].i=i;
if(i+len<=n)//如果有第二关键字就记录
d[i].key2=rk[i+len];
else d[i].key2=0;//没有就将优先级变为最高
}
sort(d+1,d+1+n,cmp);//快排
int rank=1;
rk[d[1].i]=rank;
For(i,2,n){//合并第一第二关键字
if(d[i].key1==d[i-1].key1&&d[i].key2==d[i-1].key2)
rk[d[i].i]=rank;
else rk[d[i].i]=++rank;
}
if(rank==n)break;//如果排名已经都不相同了就退出循环
}
For(i,1,n)sa[rk[i]]=i;
}
signed main(){
cin>>s;
s=' '+s;
n=s.size()-1;
SA();
For(i,1,n)printf("%lld ",sa[i]);
return 0;
}
基数排序
可以直接把上面快排的部分直接换成基数排序。
Code
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+5;
int sa[maxn], rank[maxn], newRank[maxn], sum[maxn], key2[maxn];
int n, m;
char str[maxn];
bool cmp(int a, int b, int l){
if(rank[a] != rank[b]) return false;
if( (a+l > n and b+l <= n) or (a+l <= n and b+l > n) ) return false;
if(a+l > n and b+l > n) return true;
return rank[a+l] == rank[b+l];
}
int main(){
scanf("%s", str+1);
n = strlen(str+1);
for(int i=1; i<=n; i++) sum[rank[i] = str[i]]++;
m = max(n, 256);
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];
for(int i=n; i>=1; i--) sa[sum[rank[i]]--] = i;
for(int l=1; l<n; l<<=1){
int k = 0;
for(int i=n-l+1; i<=n; i++) key2[++k] = i;
for(int i=1; i<=n; i++) if(sa[i] > l) key2[++k] = sa[i]-l;
for(int i=1; i<=m; i++) sum[i] = 0;
for(int i=1; i<=n; i++) sum[rank[i]]++;
for(int i=1; i<=m; i++) sum[i]+=sum[i-1];
for(int i=n; i>=1; i--){
int j = key2[i];
sa[sum[rank[j]]--] = j;
}
int rk = 1;
newRank[sa[1]] = rk;
for(int i=2; i<=n; i++){
if(cmp(sa[i-1], sa[i], l)) newRank[sa[i]] = rk;
else newRank[sa[i]] = ++rk;
}
for(int i=1; i<=n; i++) rank[i] = newRank[i];
if(rk == n) break;
}
for(int i=1; i<=n; i++) printf("%d ",sa[i]);
return 0;
}
