主席树学习笔记
什么是主席树
主席树这个名字看上去很高级，其实不然，它还有另一个名字——可持久化线段树。
什么是可持久化
可持久化顾名思义就是它可以变得持久，就是我们对他不断进行单点修改后，突然查询它的某一个历史版本，这就叫可持久化。
引入例题
题目大意
如题，你需要维护这样的一个长度为 \(N\ (1\le N\le 10^6)\) 的数组，支持如下几种操作
-
1.在某个历史版本上修改某一个位置上的值
-
2.访问某个历史版本上的某一位置的值
此外，每进行一次操作（对于操作 2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从 1 开始编号，版本 0 表示初始状态数组）
此时我们就需要用到主席树了。
分析
问题：这里我们为什么不能直接用数组来做？
很简单，如何我们用数组来做的话每改变一个数，我们就要新建一个数组并将其他没有改变的也一起复制下来，而\(1\le N \le 10^6\) 空间不支持。（如果可以就没必要做了）
思考：问什么明明只修改了一个数，却必须将其他的数也复制一遍？
那是因为数组的一级索引所决定的。
什么是索引
索引是一种单独的、物理的对数据库表中一列或多列的值进行排序的一种存储结构，它是某个表中一列或若干列值的集合和相应的指向表中物理标识这些值的数据页的逻辑指针清单。
索引的作用相当于图书的目录，可以根据目录中的页码快速找到所需的内容。
最优索引
问题：怎样的索引是最高效呢？
这里，我们设索引大小为 \(k\),那么索引的层数为 \(\log_kn\),则每次修改的数量为 \(k\log_kn\)。
\(k\log_kn=\log_kn^k=k\dfrac{\log n}{\log k}=\log n\dfrac{k}{\log k}\)
设\(f(n)=\dfrac{k}{\log k}\)
\(f'(n)=\dfrac{\log k+1}{\log^2 k}=\left(\dfrac{1}{\log k}\right)^2+\dfrac{1}{\log k}\)
在 \(1\le k\le n\) 的情况下，\(\log k\in\left[0,\infty\right]\)。
所以 \(k_{\min}=e\ (\log k=1)\)。
即索引为 \(k=2\) 或 \(k=3\) 时最优。
这里我们取 \(k=2\),因为它可以用线段树维护。
算法
原理
我们想要支持回退操作就需要对每一次修改操作都进行一次复制，将一些未进行操作也进行复制，这样就可以访问到旧版本的线段树了。
那我们来分析一下单点修改时那些需要复制：
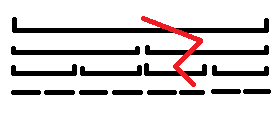
所以每一次修改我们只需要修改 \(\log n\) 个点，像这样：
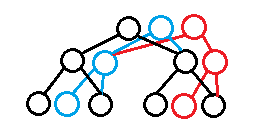
每一次都只修改被影响的点就可以。
从这张图中，我们就发现主席树的一些性质：
-
增加的非叶结点的儿子一个是其他版本的节点，一个是新节点。
-
主席树有很多根
-
对于每一个根下面都是一棵完整的线段树
-
节点都有可能有很多父节点
具体实现
-
每次增加新节点直接开一块空间新节点，编号为总节点数个数+1
-
用结构体来存子节点编号
-
访问子节点时，不是像线段树一样乘2或乘2+1，而是在结构体存子节点编号
-
每次新开个数组存根。
模版代码(P3919)
#include<bits/stdc++.h>
#define Mod 1000000007
#define int long long
#define For(i,j,k) for(int i=j;i<=k;++i)
#define FOR(i,j,k) for(int i=j;i>=k;i--)
#define mid ((l+r)>>1)
#define N 1000006
using namespace std;
int a[N],n,m,Q,root[N<<5];
struct PST{
int lc[N<<5],rc[N<<5],val[N<<5],cnt;
void build(int &x,int l,int r){
x=++cnt;
if(l==r){
val[x]=a[l];
return ;
}
build(lc[x],l,mid);
build(rc[x],mid+1,r);
}
void ins(int &x,int k,int l,int r,int L,int R){
x=++cnt;
lc[x]=lc[k];
rc[x]=rc[k];
val[x]=val[k];
if(l==r){
val[x]=R;
return ;
}
if(L<=mid)ins(lc[x],lc[k],l,mid,L,R);
else ins(rc[x],rc[k],mid+1,r,L,R);
}
int query(int x,int l,int r,int k){
if(l==r)return val[x];
if(k<=mid)return query(lc[x],l,mid,k);
else return query(rc[x],mid+1,r,k);
}
}T;
signed main(){
cin>>n>>m;
For(i,1,n)cin>>a[i];
T.build(root[0],1,n);
For(i,1,m){
int k,opt,x,y;
cin>>k>>opt>>x;
if(opt==1){
cin>>y;
T.ins(root[i],root[k],1,n,x,y);
}
if(opt==2){
cout<<T.query(root[k],1,n,x)<<endl;
root[i]=root[k];
}
}
return 0;
}
