递归问题
习题
T2:
把有 \(n\) 个圆盘的塔从左边的桩柱 \(A\) 移动到右边的桩柱 \(B\) , 不允许在 \(A\) 和 \(B\) 之间直接移动, 求最短的移动序列. ( 每一次的移动都必须是移动到中间的桩柱或者从中间的桩柱移出. 像通常一样, 较大的圆盘永远不能放在较小圆盘的上面. )
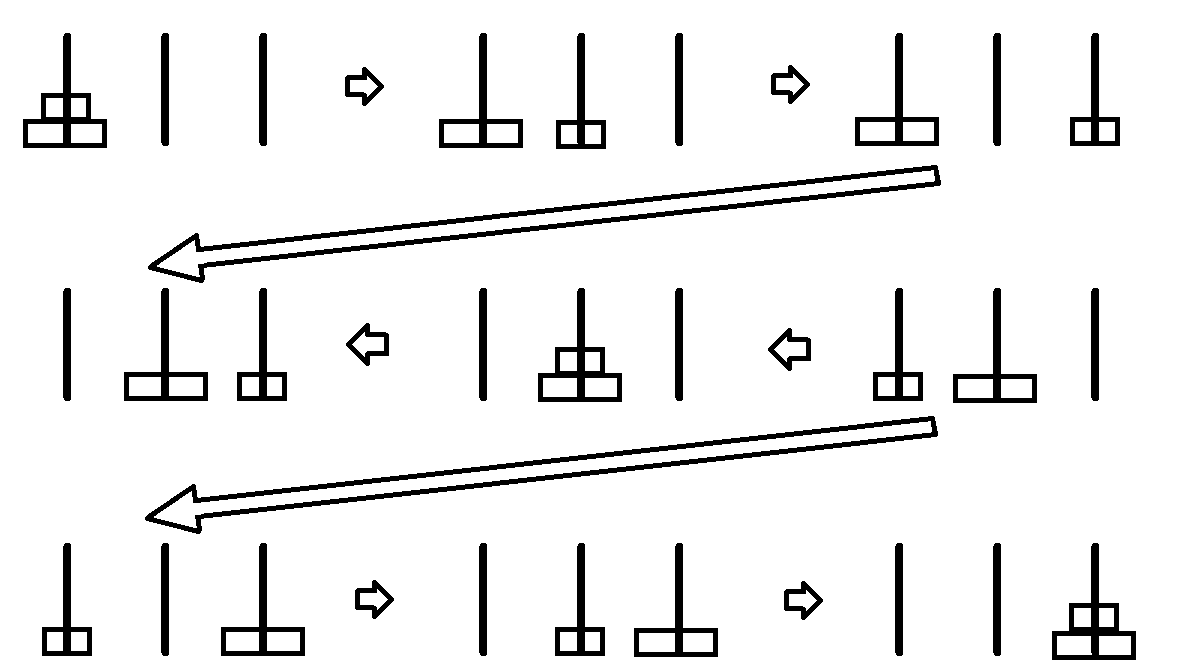
上图为大小为 \(2\) 的塔的移动方式.
若用较大的盘代表底盘, 较小的盘代表其余的盘组成的塔, 则可以表示所有大小大于等于 \(2\) 的塔的移动方式. 可以发现,每次将整座塔移动一步, 都需要移动 \(3\) 次小塔和 \(1\) 次底盘.
设 \(S_n\) 为大小为 \(n\) 的塔移动一步的最小移动次数, 则由上图可知
\[ S_n=\left\{
\begin{array}{l}
1&n=1\\
3\times S_{n-1}+1&n\geq 2\\
\end{array} \right. \]
所以
\[S_n= \frac{3^n-1}{2}
\]
答案为 \(2\times S_n=3^n-1\)
T6:
平面上由 \(n\) 条直线定义的某些区域是无界的, 而另一些区域则是有界的. 有界区域的最大个数是多少?
设 \(S_n\) 为 \(n\) 条直线能确定的有界区域的最大可能个数.
显然 \(S_1=S_2=0\) .
对于加进来的第 \(n\) 条直线, 与其他直线最多有 \(n-1\) 个交点, 于是被分成 \(n\) 段, 每段都对应新划分出的一个区域. 其中两端的两段是射线, 对应的区域是无限区域.
所以可知每次新增 \(n-2\) 个有界区域.
所以可知
\[S_n=\left\{
\begin{array}{l}
0&n\leq 2\\
S_{n-1}+n-2&n>2
\end{array}\right.\]
所以
\[S_n=\frac{1}{2}n^2-\frac{3}{2}n+1
\]
T7:
设 \(H(n)=J(n+1)-J(n)\). 方程 \((1.8)\) 告诉我们有 \(H(2n)=2\) , 而对 \(n\geq 1\) 有 \(H(2n+1)=J(2n+2)-J(2n+1)=(2J(n+1)-1)-(2J(n)+1)=2H(n)-2\). 于是, 看起来有可能通过对 \(n\) 用归纳法, 证明对所有 \(n\) 都有 \(H(n)=2\). 这里什么地方有错?
\(H(2n+1)=2H(n)-2\nRightarrow H(2n+1)=2\)
T8:
\(Q_0=\alpha;~Q_1=\beta;\\Q_n=(1+Q_{n-1})/Q_{n-2},(n>1)\)
假设对于所有 \(n\geq 0\) , \(Q_n\neq0\). 提示:\(Q_4=(1+\alpha)/\beta\).
\(Q=\{\alpha,\beta,\frac{1+\beta}{\alpha},\frac{1+\alpha+\beta}{\alpha\beta},\frac{1+\alpha}{\beta},\alpha,\beta,\dots\}\)
显然,函数 \(Q\) 是周期函数, 周期大小为 \(5\) .
T9:
有时用向后归纳是可能的, 采用从 \(n\) 到 \(n-1\)来证明而不是从 \(n-1\) 到 \(n\). 例如, 考虑命题
\[P(n):if(x,\dotsb,x_n\geq 0),~x_1\dotsb x_n\leq(\frac{x_1+\dotsb+x_n}{n})^n.
\]
由于 \((x_1+x_2)^2-4x_1x_2=(x_1-x_2)^2\geq0\) , 所以当 \(n=2\) 时, 这是真的.
\((a)\) . 通过置 \(x_n=(x+\dotsb+x_{n-1})/(n-1)\) , 证明 \(\forall n>1\) , \(P(n)\) 蕴涵 \(P(n-l)\) .
\[x_1\dotsb x_n\leq(\frac{x_1+\dotsb+x_n}{n})^n\\
=(\frac{(x_1+\dotsb+x_{n-1})\cdot\frac{1+(n-1)}{n-1}}{n})^n=(\frac{x_1+\dotsb+x_{n-1}}{n-1})^n\]
\[\therefore x_1\dotsb x_{n-1}\cdot\frac{x+\dotsb+x_{n-1}}{n-1}=(\frac{x_1+\dotsb+x_{n-1}}{n-1})^n
\]
\[\therefore P(n-1):x_1\dotsb x_{n-1}\cdot=(\frac{x_1+\dotsb+x_{n-1}}{n-1})^{n-1}
\]
\((b)\) . 证明 \(P(n)\) 和 \(P(2)\) 蕴涵 \(P(2n)\) .
由 \(x_1,\dotsb,x_{2n}\geq 0\), 可知计算过程中所有数均大于等于 \(0\) .
已知 \(P(2) \And P(n)\) 成立, 可得:
\[x_1\dotsb x_n\leq(\frac{x_1+\dotsb+x_n}{n})^n, x_{n+1}\dotsb x_{2n}\leq(\frac{x_{n+1}+\dotsb+x_{2n}}{n})^n\\
\Rightarrow x_1\dotsb x_n\cdot x_{n+1}\dotsb x_{2n}\leq(\frac{x_1+\dotsb+x_n}{n})^n\cdot(\frac{x_{n+1}+\dotsb+x_{2n}}{n})^n\\
\leq(\frac{\frac{x_1+\dotsb+x_n}{n}+\frac{x_{n+1}+\dotsb+x_{2n}}{n}}{2})^{2n}=(\frac{x_1+\dotsb+x_{2n}}{2n})^{2n}\]
即 \(P(2n)\) 成立.
\((c)\) . 阐明为什么对所有 \(n\) 蕴涵着 \(P(n)\) 的真实性.
显然, \(P(1)\) 与 \(P(2)\) 为真, 由 \((b)\) 可得, \(P(2^n)\) 均为真.
\(\therefore\forall n>1,~P(2^{n+1})\Rightarrow P(2^{2n+1}-1)\Rightarrow\dotsb\Rightarrow P(2^{n+1}-2^n+1)\)
T11:
双重河内塔包含 \(2^n\) 个圆盘, 它们有 \(n\) 种不同的尺寸, 每一种尺寸的圆盘有两个. 如通常那样, 要求每次只能移动一个圆盘, 且不能把较大的圆盘放在较小的圆盘上面.
\((a)\) 如果相同尺寸的圆盘是相互不可区分的,要把一个双重塔从一根桩柱移动到另一根桩柱需要移动多少次?
用 \(A_n\) 来表示双重河内塔的最少移动次数, \(T_n\) 表示普通河内塔的最少移动次数.
显然, \(A_n=2T_n=2^{2n+1}-2\) .
\((b)\) 如果在最后的排列中要把所有同样尺寸的圆盘恢复成原来的从上到下的次序, 需要多少次移动?
设 \(B_n\) 是最少移动次数, \(B(1)=3\). 可以证明, 当 \(n>1\) 时任何策略都做不到优于 \(B_n=A_{n-1}+2+A_{n-1}+2+B_{n-1}\) .
以上为标准答案, 然而我不会做.
T12:
我们进一步推广习题 \(11a\) . 假设圆盘具有 \(n\) 种不同的尺寸, 且恰好有 \(m_k\) 个圆盘的尺寸是 \(k\) . 当相同尺寸的圆盘被视为不可区分的时候, 确定移动一个塔所需要的最少移动次数 \(A(m_1,\dotsb,m_n)\) .
\[A(m_1,\dotsb,m_n)=2A(m_1,\dotsb,m_{n-1},0)+m_n\\=4A(m_1,\dotsb,m_{n-2},0,0)+2m_{n-1}+m_n\\=\dotsb=\sum_{i=1}^n2^{n-i}\cdot m_i
\]
T14:
在一块厚奶酪上划出五道直的切痕, 可以得到多少块奶酪? ( 在你划切痕时, 奶酪必须保持在它原来的位置上,且每道切痕必定与三维空间中的一个平面相对应. ) 对 \(P_n\) 求一个递归关系, 这里 \(P_n\) 表示 \(n\) 个不同的平面所能定义的三维区域的最大个数.
\[P_0=1\\
P_n=P_{n-1}+L_{n-1}\\=P_{n-1}+\frac{n^2-n}{2}+1\\
=P_{n-2}+\frac{(n-1)^2-(n-1)+n^2-n}{2}+2\\
=\dotsb\\
=P_0+\frac{1^2+\dotsb+n^2-(1+\dotsb+n)}{2}+n\\
=n+1+\frac{\frac{n(n+1)(2n+1)}{6}-\frac{n(n+1)}{2}}{2}\\
=\frac{1}{6}n^3+\frac{5}{6}n+1\]
T15:
约瑟夫有一个朋友, 他站在倒数第二的位置上因而获救. 当每隔一个人就有一人被处死时, 倒数第二个幸存者的号码 \(I(n)\) 是多少?
\(I=undefined,2,1,3,5,1,3,5,7,9,11,1,3,5,7,9,11,13,15,17,19,21,23,1,\dotsb\)
T16:
用成套方法来解一般的四参数递归式
\[g(1)=\alpha~;\\g(2n+j)=3g(n)+\gamma n+\beta_j~;~~j=0,1~;~~n\geq1.
\]
提示: 尝试用函数 \(g(n)=n\) .
\[设~g(n)=A(n)\alpha+B_0(n)\beta_0+B_1(n)\beta_1+C(n)\gamma~;\\
将~g(n)=A(n)~代入,~可得:\\
A(n)=A(n)\alpha+B_0(n)\beta_0+B_1(n)\beta_1+C(n)\gamma\\
\therefore(\alpha,\beta_0,\beta_1,\gamma)=(1,0,0,0)\\
\therefore\left\{
\begin{array}{l}
A(1)=1\\
A(2n)=A(2n+1)=3A(n)
\end{array}\right.\\
\therefore A(2^m+j)=3^m~;~~m\geq0,0\leq j<2^m\\
将~g(n)=C(n)~代入,~可得:\\
C(n)=C(n)\alpha+B_0(n)\beta_0+B_1(n)\beta_1+C(n)\gamma\\
\therefore(\alpha,\beta_0,\beta_1,\gamma)=(0,0,0,1)\\
\therefore\left\{
\begin{array}{l}
C(1)=0\\
C(2n)=C(2n+1)=3C(n)+n
\end{array}\right.\\
\therefore C((b_mb_{m-1}\dotsb b_1b_0)_2)=3C((b_mb_{m-1}\dotsb b_2b_1)_2)+(b_mb_{m-1}\dotsb b_2b_1)_2\\
=9C((b_mb_{m-1}\dotsb b_3b_2)_2)+3(b_mb_{m-1}\dotsb b_3b_2)_2+(b_mb_{m-1}\dotsb b_2b_1)_2\\
=\dotsb\\
=3^mC((b_m)_2)+3^{m-1}(b_m)_2+\dotsb+3^0(b_mb_{m-1}\dotsb b_2b_1)_2\\
=3^m+\sum_{i=1}^mb_i\sum_{j=0}^{i-1}3^j~;~~(b_m=1)\\
将~g(n)=1~代入,~可得:~\left\{
\begin{array}{l}
1=\alpha~;\\
1=3+\gamma n+\beta_0\\
1=3+\gamma n+\beta_1
\end{array}\right.\\
\therefore (\alpha,\beta_0,\beta_1,\gamma)=(1,-2,-2,0)\\
\therefore A(n)-2B_0(n)-2B_1(n)=1\\
将~g(n)=n~代入,~可得:~\left\{
\begin{array}{l}
1=\alpha~;\\
2n=3n+\gamma n+\beta_0\\
2n+1=3n+\gamma n+\beta_1
\end{array}\right.\\
\therefore (\alpha,\beta_0,\beta_1,\gamma)=(1,0,1,-1)\\
\therefore A(n)+B_1(n)-C(n)=n\\
综上, 可得:~\left\{
\begin{array}{l}
A(2^m+j)=3^m&m\geq0,0\leq j<2^m\\
C((b_mb_{m-1}\dotsb b_1b_0)_2)=3^m+\sum_{i=1}^mb_i\sum_{j=0}^{i-1}3^j&b_m=1\\
A(n)-2B_0(n)-2B_1(n)=1&n\geq1\\
A(n)+B_1(n)-C(n)=n&n\geq1
\end{array}\right.\\
接下来直接解方程即可.
%~\left\{
% \begin{array}{l}
% A((b_mb_{m-1}\dotsb b_1b_0)_2)=3^m\\
% C((b_mb_{m-1}\dotsb b_1b_0)_2)=3^m+\sum_{i=1}^mb_i\sum_{j=0}^{i-1}3^j\\
% A((b_mb_{m-1}\dotsb b_1b_0)_2)-2B_0((b_mb_{m-1}\dotsb b_1b_0)_2)-2B_1((b_mb_{m-1}\dotsb b_1b_0)_2)=1\\
% A((b_mb_{m-1}\dotsb b_1b_0)_2)+B_1((b_mb_{m-1}\dotsb b_1b_0)_2)-C((b_mb_{m-1}\dotsb b_1b_0)_2)=(b_mb_{m-1}\dotsb b_1b_0)_2
% \end{array}\right.b_m=1
\]
T18:
当有 \(4\) 根而不是 \(3\) 根桩柱时, 如果 \(W_n\) 是将一个有 \(n\) 个圆盘的塔从一根桩柱移动到另一根桩柱所需要的最少移动步数, 证明
\[W_{n(n+1)/2}\leq2W_{n(n-1)/2}+T_n,~~n>0.
\]
( 这里 \(T_n=2^n-1\)是 \(3\) 根桩柱时所需要的最少移动次数. ) 利用这个结果求出 \(f(n)\) 的一个封闭形式, 使得对所有 \(n\geq0\) 都有 \(W_{n(n+1)/2}\leq f(n)\)
T19:
当每一个锯齿的角度为 \(30\degree\) 时, 有可能由 \(n\) 条折线得到 \(Z_n\) 个区域吗?
T20:
用成套方法来解一般的四参数递归式
\[h(1)=\alpha~;\\h(2n+j)=4h(n)+\gamma_j n+\beta_j~;~~j=0,1~;~~n\geq1.
\]
提示: 尝试用函数 \(h(n)=n\) 和 \(h(n)=n^2\) .
和式
和式和递归式
\[a_nT_n=b_nT_{n-1}+c_n\\
求出求和因子~s_n~满足~s_nb_n=s_{n-1}a_{n-1}\\
s_na_nT_n=s_nb_nT_{n-1}+s_nc_n\\
记~S_n=s_na_nT_n~,~可得~S_n=S_{n-1}+s_nc_n\\
\therefore S_n=s_0a_0T_0+\sum_{k=1}^{n}s_kc_k=s_1b_1T_0+\sum_{k=1}^{n}s_kc_k\\
\therefore T_n=\frac{1}{s_na_n}(s_1b_1T_0+\sum_{k=1}^{n}s_kc_k).\\
可以发现~s_n=\frac{a_{n-1}a_{n-2}\dotsb a_1}{b_nb_{n-1}\dotsb b_2}~满足求和因子的条件.\\
注:~需防止~a~或~b~中存在~0~.
\]
" 快速排序" 的比较步骤的平均次数的递归式为:
\[C_0=C_1=0~;\\C_n=n+1+\frac{2}{n}\sum_{k=0}^{n-1}C_k~,~~n>1.
\]
\[\times n~避免除法:~nC_n=n^2+n+2\sum_{k=0}^{n-1}C_k\\
作差规避~\Sigma:\\nC_n-(n-1)C_{n-1}=n^2+n+2\sum_{k=0}^{n-1}C_k-((n-1)^2+(n-1)+2\sum_{k=0}^{(n-1)-1}C_k)\\
=2n+2C_{n-1}\\
\therefore 原递归式可转化为:~\\
C_0=C_1=0~;~~C_2=3~;\\
nC_n=(n+1)C_{n-1}+2n~,~~n>2\\
于是便可以用之前的方法了.\\
s_n=\frac{a_{n-1}a_{n-2}\dotsb a_1}{b_nb_{n-1}\dotsb b_2}=\frac{(n-1)(n-2)\dotsb1}{(n+1)n\dotsb3}=\frac{2}{n(n+1)}\\
显然~s_n~满足s_n\cdot(n+1)=s_{n-1}\cdot (n-1)\\
s_n\cdot nC_n=s_n\cdot(n+1)C_{n-1}+s_n\cdot 2n~,~~n>2\\
记~S_n=s_n\cdot nC_n~,~则\\
S_n=S_{n-1}+2s_nn=S_{n-1}+\frac{4}{n+1}\\
\therefore S_n=S_2+4\sum_{k=3}^{n}\frac{1}{k+1}\\
=\frac{1}{3}\cdot2\cdot3+4\sum_{k=1}^{n}\frac{1}{k+1}-4(\frac{1}{2}+\frac{1}{3})=4\sum_{k=1}^{n}\frac{1}{k+1}-\frac{4}{3}~,~~n>2\\
\therefore C_n=\frac{1}{s_nn}S_n=\frac{n+1}{2}S_n\\=2(n+1)\sum_{k=1}^{n}\frac{1}{k+1}-\frac{2}{3}(n+1)~,~~n>2
\]
规定 调和数 \(H_n=1+\frac{1}{2}+\dotsb+\frac{1}{n}=\sum_{k=1}^n\frac{1}{k}\) .
显然, 可以用 \(H_n\) 来表达 \(C_n\).
\[C_n=2(n+1)H_n-\frac{8}{3}n-\frac{2}{3}~,~~n>1
\]
和式的处理
\[\sum_{k\in K}c\cdot a_k=c\sum_{k\in K}a_k~;~~(~分配律)\\
\sum_{k\in K}(a_k+b_k)=\sum_{k\in K}a_k+\sum_{k\in K}~;~~(~结合律)\\
\sum_{k\in K}a_k=\sum_{p(k)\in K}a_{p(k)}~;~~(~交换律)
\]
若 \(K\) 和 \(K'\) 为整数的任意集合
\[\sum_{k\in K}a_k+\sum_{k\in K'}a_k=\sum_{k\in K\cap K'}a_k+\sum_{k\in K\cup K'}a_k
\]
等差级数的一般和
\[S=\sum_{0\leq k\leq n}(a+b_k)\Rightarrow S=\sum_{0\leq n-k\leq n}(a+b(n-k))=\sum_{0\leq k\leq n}(a+bn-bk)\\
\therefore2S=\sum_{0\leq k\leq n}((a+bk)+(a+bn-bk))=\sum_{0\leq k\leq n}(2a+bn)\\
=(2a+bn)\sum_{0\leq k\leq n}1=(2a+bn)(n+1).\\
\therefore \sum_{k=0}^{n}(a+bk)=(a+\frac{1}{2}bn)(n+1)
\]
扰动法
令
\[S_n=\sum_{0\leq k\leq n}a_k
\]
于是可以改写 \(S_{n+1}\) ;
\[S_n+a_{n+1}=\sum_{0\leq k \leq n+1}a_k=a_0+\sum_{0\leq k\leq n}a_{k+1}
\]
若可以用 \(S_n\) 来表示 \(\sum_{0\leq k\leq n}a_{k+1}\), 就可以得到一个方程, 解便是我们求的和式.
比如 几何级数 ( 等差数列求和 ) :
\[S_n=\sum_{0\leq k\leq n}ax^k
\]
通过扰动法可得:
\[S_n+ax^{n+1}=ax^0+\sum_{0\leq k\leq n}ax^{k+1}
\]
显然, \(\sum_{0\leq k\leq n}ax^{k+1}=xS_n\)
\[\therefore S_n+ax^{n+1}=a+xS_n\\
\therefore S_n=\frac{a-ax^{n+1}}{1-x}
\]
多重和式
\[A=\begin{bmatrix}
a_1a_1&a_1a_2&a_1a_3&\dotsb&a_1a_n\\
a_2a_1&a_2a_2&a_2a_3&\dotsb&a_2a_n\\
a_3a_1&a_3a_2&a_3a_3&\dotsb&a_3a_n\\
\vdots&\vdots&\vdots&\ddots&\vdots\\
a_na_1&a_na_2&a_na_3&\dotsb&a_na_n
\end{bmatrix}\\
\]
目标求出
\[\sum_{1\leq j\leq k\leq n}a_ja_k
\]
的一个简单的公式.
\[\sum_{1\leq j\leq k\leq n}a_ja_k=\sum_{1\leq k\leq j\leq n}a_ka_j=\sum_{1\leq k\leq j\leq n}a_ja_k\\
\because [1\leq j\leq k\leq n]+[1\leq k \leq j\leq n]=[1\leq j,k\leq n]+[1\leq j=k\leq n]\\
\therefore \sum_{1\leq j\leq k\leq n}a_ja_k=\frac{1}{2}(\sum_{1\leq j\leq k\leq n}a_ja_k+\sum_{1\leq k\leq j\leq n}a_ja_k)\\
=\frac{1}{2}(\sum_{1\leq j,k\leq n}a_ja_k+\sum_{1\leq j=k\leq n}a_ja_k)\\
=\frac{1}{2}((\sum_{k=1}^{n}a_k)^2+\sum_{k=1}^{n}a_k^2).
\]
习题
T19
利用求和因子来求解递归式
\[T_0=5~;\\2T_n=nT_{n-1}+3\times n!
\]
\[令求和因子~s_n=\frac{a_{n-1}a_{n-2}\dotsb a_1}{b_nb_{n-1}\dotsb b_2}=\frac{2^{n-1}}{n!}\\
s_n\cdot2T_n=s_n\cdot nT_{n-1}+s_n\cdot3\cdot n!\\
令~S_n=s_n\cdot2T_n=\frac{2^n}{n!}T_n\\
\therefore S_n=S_{n-1}+\frac{2^{n-1}}{n!}\cdot3\cdot n!=S_{n-1}+3\cdot2^{n-1}\\
=S_0+\sum_{k=1}^{n}3\cdot2^{k-1}=\frac{2^{-1}}{0!}\cdot2T_0+3\cdot\frac{1-2^n}{1-2}\\
=2+3\cdot2^n~,~~n\geq1\\
\therefore S_n=2+3\cdot2^n~,~~n\geq0\\
\therefore T_n=\frac{1}{2s_n}S_n=\frac{n!}{2^n}(2+3\cdot2^n)\\
\therefore T_n=\frac{n!}{2^{n-1}}+3\cdot n!~,~~n\geq0
\]
T20
试用扰动法计算 \(\sum_{k=0}^{n}kH_k\) , 不过改为推导出 \(\sum_{k=0}^{n}H_k\) 的值.
\[\sum_{k=0}^{n}kH_k+(n+1)H_{n+1}=\sum_{k=0}^{n+1}kH_k\\
=\sum_{k=0}^{n}(k+1)H_{k+1}\\
=\sum_{k=0}^{n}kH_k+\sum_{k=0}^{n}H_k+\sum_{k=0}^{n}(k+1)\frac{1}{k+1}\\
=\sum_{k=0}^{n}kH_k+\sum_{k=0}^{n}H_k+n+1\\
\therefore (n+1)H_{n+1}=\sum_{k=0}^{n}H_k+n+1\\
\therefore \sum_{k=0}^{n}H_k=(n+1)(H_{n+1}-1)
\]
T21
假设 \(n\geq 0\) , 用扰动法计算和式 \(S_n=\sum_{k=0}^{n}(-1)^{n-k}\) , \(T_n=\sum_{k=0}^{n}(-1)^{n-k}k\) 以及 \(U_n=\sum_{k=0}^{n}(-1)^{n-k}k^2\) .




